基于RBF神经网络的建筑物沉降预测

吴 晓，朱军桃，李朋成

（1.桂林理工大学 测绘地理信息学院 广西空间信息与测绘重点实验室，广西 桂林 541004）

径向基函数(RBF)人工神经网络作为一种新颖有效的前馈式神经网络,具有较高的运算速度，更好的逼近能力以及全局最优特性，特别是它较强的非线性映射能力,能以任意精度全局逼近一个非线性函数,使其在很多领域都得到了广泛应用[1]。本文的实例分析正是采用了RBF 神经网络的建模方法来对建筑物的沉降进行预测的。

1 径向基函数神经网络

1.1 RBF神经网络原理

人工神经网络因其广泛的适应和学习能力, 在非线性系统的预测中得到推崇。RBF神经网络是由Moody J和Darken C于20 世纪 80 年代末提出的一种神经网络结构[2]。它是基于人脑的神经元细胞对外界反应的局部性而提出的, 是一种新颖、有效的前馈式神经网络，在逼近能力、分类能力及学习速度等方面均优于BP神经网络。

RBF神经网络一般是由输入层、隐层和输出层构成的3层前向神经网络,其拓扑结构如图1所示,输入层节点仅传递输入信号到隐层，隐层神经元一般采用高斯函数作为径向基函数，而输出层节点则通常是简单的线性函数。当输入信号靠近基函数中央范围时，隐层节点才会产生较大的输出信号，由此可以看出该网络具有局部逼近能力，因此RBF网络又称为局部感知场网络[3]。

神经网络信息的传输路径为：输入层只负责信息的传输,其输入与输出相同；隐层中每个神经元将自己和输入层神经元相连的连接权值矢量W1i（也称为第i个隐层神经元的基函数中心）与输入矢量Xq（第q个输入矢量，Xq=X1q，X2q，X3q，…，Xjq，…,Xmq）之间的距离乘以本身的偏置值b1i作为自己的输入,见图2。可见,对应输入层第q个输入产生的隐层第i个神经元的输入为:

隐层第i个神经元的输入经过高斯函数的变换产生的输出为：

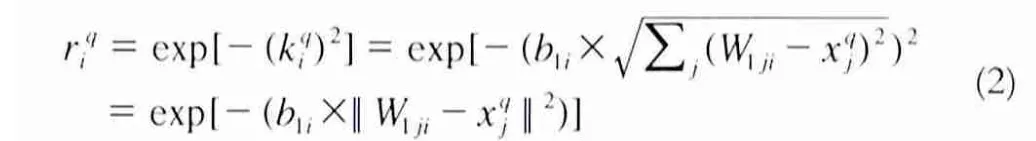
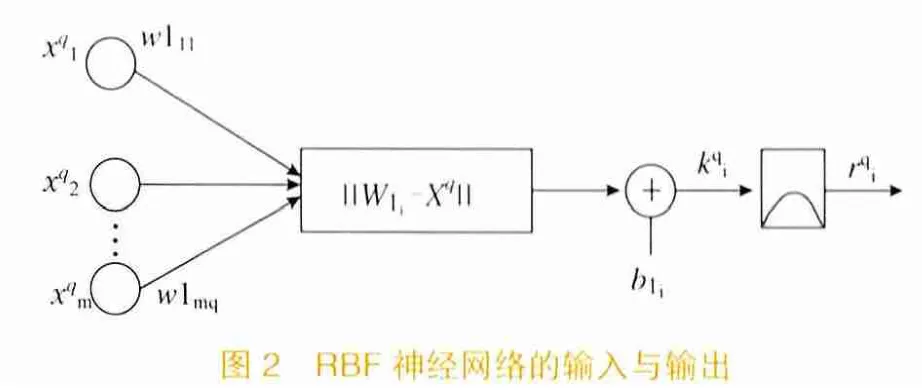
理论表明,对于任意一个给定的非线性函数, 可用RBF神经网络以任意精度全局逼近它。RBF网络还能够避免输入层与隐层间反向传播的繁琐冗长的计算, 可使学习比通常的BP神经网络快1 000～10 000倍。

1.2 RBF网络建模

RBF网络用于非线性系统辨识和系统建模的步骤如下：

1）选择恰当的学习样本。在许多文献中，系统辨识的学习数据都是用伪随机码激励系统得到，但在过程控制中，这是不适用的。无论采用什么方法得到的学习数据都必须遵循一条原则，即学习样本必须充分体现系统的工作状况。

2）学习样本数据的预处理。通常学习数据都应作归一化处理，同时由于在实时控制中采集到的数据含有噪声,因此有必要作滤波处理。

3）确定模型的阶次。可以应用被建模系统的先验知识来确定，也可通过数据分析得到。

4） 采用恰当的学习算法完成RBF网络的离线学习。

5）倘若系统是时变的，必须用递推算法对RBF网络进行在线校正。

2 工程应用

2.1 工程概况

工程工地位于桂林市临桂县，此处正在修建一个大型的农贸市场，正处于开挖基坑阶段。该开挖基坑东西方向长约55 m, 南北方向长约60 m，开挖深度为12.5 m ，安全等级为一级；基坑周围均为6层高的居民楼，且一楼均为商铺，环境相对偏僻。为了了解基坑开挖对周围居民楼的影响状况，特别布设了一些监测点来进行沉降观测。监测点布设于基坑旁的居民楼大门的水泥柱子上，然而在工程监测的后期出现少有、连绵的冬雨，不仅给该工程的监测带来一定的难度，也为该点的监测带来了一些不必要的人为误差。本文所用数据主要是监测点1的实测值。

2.2 实测数据的预处理

本监测从2012-10-17开始至2013-01-04结束。1点的监测样本数目为N=80，利用前75个沉降值建立RBF神经网络模型，后5个沉降值作为预测的实测参考值。沉降观测点安装在基坑周边建筑物的支柱上, 在基坑开挖过程中定期观测其沉降值。通过对测点1各个时期的高程值进行一阶差分，得到沉降值。经过差分之后的数据序列成为相对平稳的序列,如表1所示。

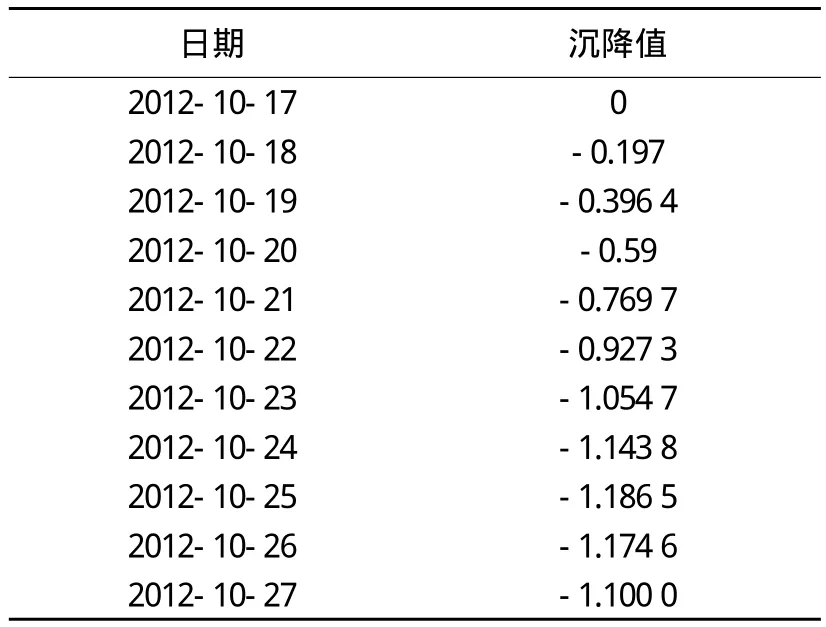
表1 观测点1的部分沉降实测值/mm

2.3 RBF神经网络模型的预测

为了更好地验证该预测模型在工程中的应用效果，分别设计了2种方案来对沉降观测数据进行建模分析。

方案1：RBF神经网络模型。对选定的样本序列,根据建模阶段设定的目标误差和均方误差最小的原则，利用Matlab 神经网络工具箱提供的Newrb函数设计一个径向基网络，它可以根据设定的最大隐藏神经元的个数，自动增加径向基网络的隐层神经元的个数，直到均方误差满足为止[4]；再将满足要求的的径向基网络应用于后期的仿真，进而计算出预测残差值；最后用建模阶段和预测阶段均方误差来衡定其预测效果。预测效果及分析如图3、表2所示。

表2 RBF神经网络预测效果及分析表

方案2：传统的回归模型。对选定的样本序列,根据均方误差最小的原则，利用Matlab 编程从阶数p=1开始到p=75自动搜索来确定回归模型的阶数，然后按照最小二乘参数法估计各阶参数,同时计算相应的系数值, 再计算预测残差值，最后用建模阶段和预测阶段均方误差（其中4e为预测残差，k为预测期数)来衡定其预测效果。预测效果及分析如图3、表3和表4所示。

图3 预测结果

表3 传统回归模型预测效果及分析表

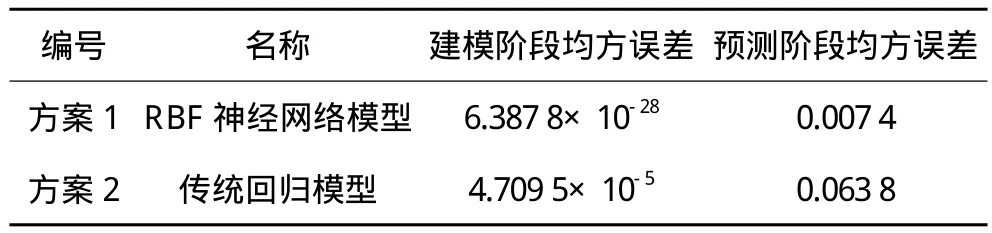
表4 2个方案预测效果对比表

由分析得知，相对于传统的回归模型,RBF神经网络模型在建模阶段和预测阶段的精度都相对较高，进一步验证了RBF 神经网络作为一种性能良好的前馈网络，具有更好的逼近能力和全局最优特性。

3 结 语

人工神经网络可以通过对样本的反复学习来反映建筑物沉降的非线性演化关系，其预测效果要优于传统回归模型的预测方法。RBF 神经网络作为一种性能良好的前馈型人工神经网络，具有更好的逼近能力和全局最优特性。

本文是RBF神经网络在建筑物沉降预报中的初步应用，工程应用实例则是以建筑物沉降时间序列为基础，采用 RBF 神经网络建立建筑物沉降预测模型，通过最近邻聚类学习算法实现建筑物沉降预测，具有结构简单、学习速度快、预测精度高的特点，网络外推能力也较强。实际应用结果表明,该方法具有十分理想的预测效果,在建筑物沉降预报中具有广泛的应用前景。

[1]王炜，吴耿锋，张博锋，等.径向基函数(RBF)神经网络及其应用[J].地震，2005(4)：20-22

[2]Moody J，Darken C. Learning with Localized Received Fields[C]. The 1988 Connectionist Models Summer School,Menlo Park，1988

[3]农吉夫，金龙.基于 MATLAB 的主成分RBF神经网络降水预报模型[J].热带气象学报，2008(12):714-716

[4]闻新，周露，王丹力,等.MATLAB神经网络应用设计[M].北京：科学出版社，2000

[5]GT/T12897-2006.国家一、二等水准测量规范[S].

[6]JGJ8-2007.建筑变形测量规范[S].

[7]曹弋.MATLAB教程及实训[M].北京：机械工业出版社，2008