RIKEN介观器件腔中粒子输运过程的混沌性质及分形自相似结构研究*
2013-09-27杨秦男张延惠蔡祥吉蒋国辉徐学友
杨秦男 张延惠† 蔡祥吉 蒋国辉 徐学友
1)(山东师范大学物理与电子科学学院,济南 250014)
2)(山东省科学院情报研究所,济南 250014)
(2012年10月10日收到;2012年12月21日收到修改稿)
1 引言
混沌及分形理论是近些年来发展起来的新型非线性理论,在很多方面有着重要研究意义[1].混沌简单来说就是研究对象系统无规行为中的规律性[2],而分形是混沌性质中存在的规律性中的一种.混沌分形与气象学、地质学以及物理学的众多分支学科有着广泛的联系,在解决非线性问题中起着重要作用.二维介观器件体系中粒子在输运过程中的诸多现象和行为都存在着混沌及分形性质,通过改变器件参数或环境(磁场等)来探究它们对粒子逃逸曲线混沌性质的影响规律,同时发现体系中存在的分形自相似结构[3-6].本文以逃逸曲线定性比较和分形维数定量计算两种手段来研究器件中混沌吸引子的变化规律;首次运用“眼式分析”和相似比比较的方法来验证逃逸曲线中存在的分形自相似结构.本文的研究对分析混沌逃逸规律、分形自相似结构以及器件输运的稳定性控制等具有理论和实际应用意义.
2 器件介绍及理论模型
本文采用的RIKENSide-wall Sinai Billard器件(图1)由日本理化研究所(RIKEN)纳米电子材料实验室的Cooper和Bird在晶圆上制得,并由新南威尔士大学的Micolich等[7]进行了低温下电子量子干涉效应等实验.为叙述简便,本文的研究中将该器件简称为RIKEN器件.
RIKEN台球器件可理解为如图2所示的二维器件模型,图中标度的量级为微米级.器件底部的两个开口很小,粒子无法通过,因此可以忽略其对粒子逃逸的影响.器件腔内部区域可视为势阱,直线和底部圆弧部分为势垒[8].粒子在器件中运动,到达开口位置时逃逸.当粒子能量增大时,粒子会从势垒上势能较低的区域逃逸,从而导致势阱面积增大(但势阱的形状基本不变),粒子的逃逸率增加,相同情况下的粒子逃逸时间也变短[9-11].本文的研究主要基于统计单个粒子逃逸前的碰撞次数,为控制变量以及简化计算过程,认为粒子只从开口处逃逸而无法从势垒逃逸,即二维器件腔内部为无限深势阱,边界势垒的势能无限大.
粒子在二维器件腔内与器件壁的碰撞视为完全弹性碰撞,碰撞前后的运动轨迹遵从反射定律[12].由于器件的对称性,可定义两侧顶端的任意一个开口为粒子的入射口.本文以下研究定义器件左侧开口为粒子入射位置,定义粒子到达器件两侧顶端任一开口位置时逃逸器件腔.

图1 RIKEN器件的电镜扫描图
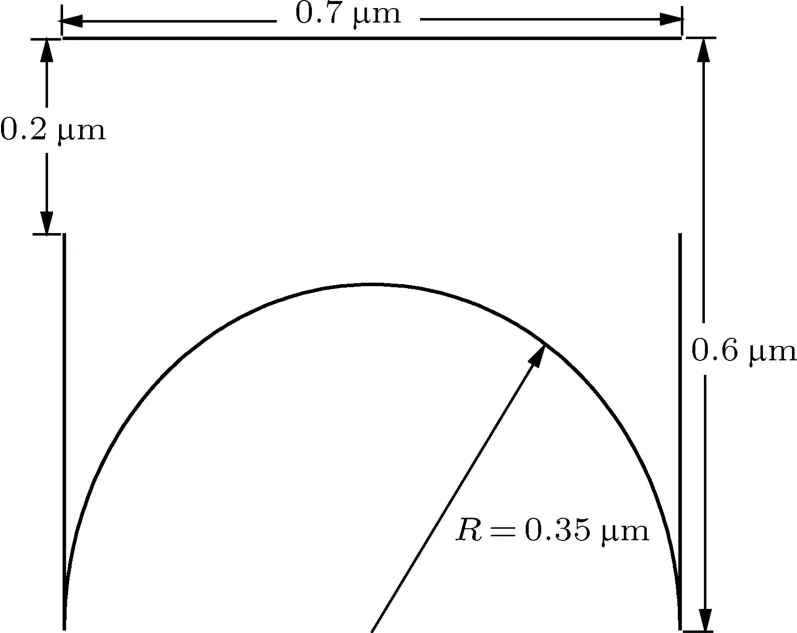
图2 RIKEN器件的理论模型
3 粒子初始位置及器件参数对输运混沌性质的影响
粒子从入射到出射的过程中会与势垒发生若干次碰撞,在器件参数(主要是开口宽度、腔长以及圆弧半径)确定的情况下,粒子逃逸前的碰撞次数由入射角度决定.当入射角度微小改变时,碰撞次数可能不会明显改变,也可能会发生剧烈变化[13].图3(a)为入射角分别为21°和22°时粒子逃逸前的碰撞情况比较,入射角的微小改变没有引起碰撞轨迹和次数的明显变化;图3(b)为入射角为41°和41.3°时粒子逃逸前的碰撞情况比较,入射角的微小改变引起了碰撞轨迹和次数的剧烈变化.这种产生碰撞次数剧烈变化时对应的角度称作奇异点,奇异点的集合就是混沌吸引子.产生这种剧烈变化的原因主要是粒子与器件底部弧线区域碰撞,当初始入射角近似相同的两个粒子到达圆弧部分时,它们反射轨迹之间的夹角及距离差异会增大,因此圆弧对微小差异起到了放大的作用(以下简称为圆弧的放大作用).随着反弹次数的增加这种差距会越来越大,最终导致了入射条件近似的粒子逃逸前碰撞次数的明显差异.当然,器件的开口边缘位置、拐角附近区域、直线区域等也会产生这种效果,下文将分别予以讨论.器件中粒子逃逸的混沌现象由此产生,这个过程称为“混沌逃逸”[3],其逃逸时间和碰撞次数等敏感依赖于粒子初始角度的改变.

图3 (a)入射角21°(实线)与22°(虚线)比较;(b)入射角41°(实线)与 41.3°(虚线)比较
图4为计算得到的随粒子入射角连续微小改变,粒子碰撞次数的变化曲线(以下简称为粒子的逃逸曲线).图中的黑色区域是粒子碰撞次数连续剧烈变化所导致,也就是奇异点所在的混沌区域;白色区域是碰撞次数变化不明显的区域.由于碰撞次数在60次以上的入射情况(图4(a))很少,混沌区域的碰撞次数多在60次以内,故而可以忽略掉60次以上的碰撞次数,只考虑60次以内的碰撞(图4(b)),本文以下研究均采用此方法.
3.1 粒子初始位置
粒子从器件的左侧开口入射,初始位置改变对应的粒子逃逸曲线变化情况如图5所示.粒子在不同初始位置下入射,其逃逸曲线中的黑色区域和白色区域分布情况基本一致,而且黑色区域所占比例不变.因此粒子初始位置改变对逃逸曲线混沌性质的影响基本可以忽略,因为逃逸曲线混沌的产生主要是由于入射角的改变,而不是粒子的初始位置.在以下各节讨论中,为控制参数单一变化,我们均默认粒子的初始入射位置为器件左侧开口的中间位置.
3.2 开口宽度
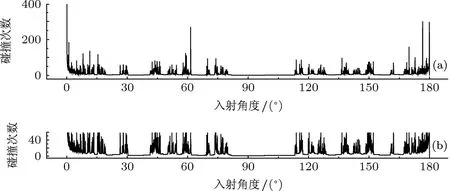
图4 RIKEN器件碰撞次数随入射角变化关系 (a)碰撞次数>60次;(b)碰撞次数<60次

图5 粒子初始位置对逃逸前碰撞次数的影响,右侧数据为粒子到开口顶端的距离
器件开口对粒子的逃逸具有选择作用,尤其是在开口边缘位置这种选择作用更明显.图3(b)中,当轨迹相近的两粒子分别到达左端开口边缘位置时,一个粒子逃逸而另一个粒子反射回器件腔无法逃逸.器件开口宽度的增大使粒子的逃逸概率增大,原逃逸过程中在开口边缘无法逃逸的粒子现在会被开口选择,逃逸器件腔.开口边缘对粒子逃逸的选择作用明显减弱,由此逃逸过程中碰撞次数的奇变点减少,逃逸曲线中的混沌区域会逐渐被白色区域取代.图6为开口宽度分别为0.05—0.30µm时的逃逸曲线比较,可以看到随开口宽度增加,白色区域逐渐增宽增多,器件中粒子逃逸曲线的混沌性减弱.
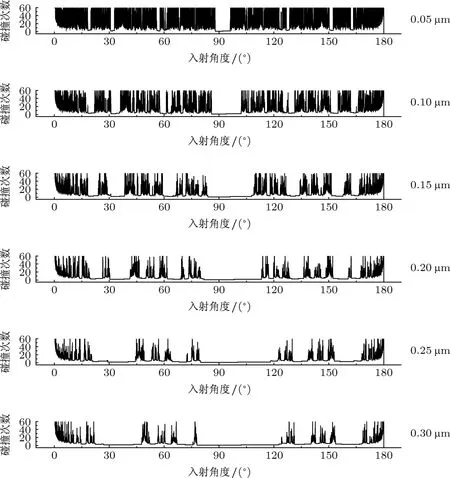
图6 开口宽度对逃逸前碰撞次数的影响,右侧数据为对应的开口宽度
3.3 器件腔长
图7 为不同腔长中粒子的逃逸曲线比较.当腔长增加时粒子逃逸前在腔内的碰撞次数增加,器件势垒的放大作用越来越明显.当粒子到达器件的开口位置时,放大的轨道差异最终体现在逃逸前的碰撞次数差异上,器件腔长的增加导致逃逸曲线混沌性的增强.
3.4 圆弧半径
器件底部圆弧半径的变化体现在两个方面:一是R≤0.35µm时弧度等于180°的半圆(如图8(a));二是R>0.35µm时弧度小于180°的圆弧(如图8(b)).
3.4.1 R≤0.35µm
图9为R≤0.35µm时器件底部圆弧半径变化时的逃逸曲线比较.在R=0时(此时器件的底部为一条直线)的粒子逃逸曲线中,入射角在0°和180°附近的碰撞次数整体较多且变化较大,存在一定的混沌性质;其他大部分角度碰撞次数没有明显的奇变,不存在混沌性质.当圆弧半径增大时,粒子到达圆弧的概率逐渐增大,圆弧区域的放大作用越来越明显,导致了粒子逃逸曲线中奇变点个数增多.因此图中的黑色混沌区域越来越宽,逃逸曲线的混沌性越来越强.

图7 器件腔长对逃逸前碰撞次数的影响,右侧数据为对应的腔长
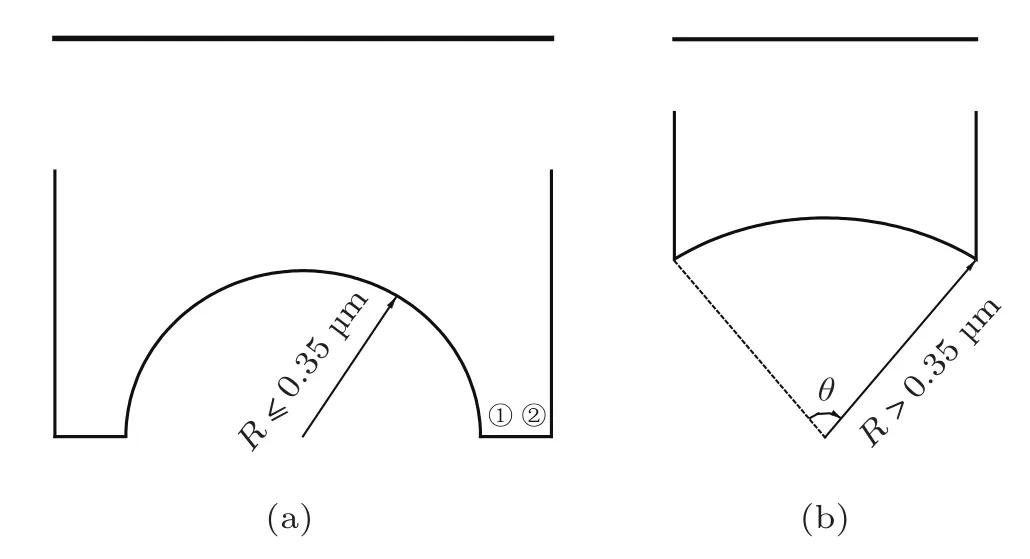
图8 (a)R≤0.35µm时器件形状示意图;(b)R>0.35µm时器件形状示意图
但是图9中的混沌区域在R=0.20µm之后并没有明显的增多,反而在R接近0.35µm时有了明显的减少.如图8(a)所示,拐角①和拐角②对粒子入射轨道的微小差距均有放大作用.R较小时两个拐角的影响是分别独立的;R较大(接近0.35µm)时,将很少有粒子在两个拐角处连续碰撞,两个拐角可视为一个拐角,其放大作用减弱.由此说明在该器件中拐角对混沌性质的影响是明显的:拐角越多越分散,器件的混沌性越强;拐角数量减少或相邻拐角距离很近时,器件的混沌性有所减弱.
3.4.2 R>0.35µm
图10为R>0.35µm时器件底部圆弧半径变化时的逃逸曲线比较.很明显,随着圆弧半径R的逐渐增大,图中的黑色区域逐渐减少,奇异点的个数下降,器件的混沌性减弱.
当R>0.35µm时,器件中拐角的数量及拐角之间的距离不再改变.圆弧的半径(或者弧度)是影响输运过程混沌性质的主要原因,半径越大(弧度越小),圆弧部分的放大效果越弱,粒子逃逸过程中碰撞次数的奇变点减少,混沌性减弱.可以预见当R→∞时,原来的弧线将逐渐变成直线,其放大作用等效于直线,其逃逸曲线将与图9中R=0时的逃逸曲线相同,因为在极限情况下两者所构造的器件形状是完全相同的.

图9 R≤0.35µm时圆弧半径对逃逸前碰撞次数的影响,右侧数据为对应的圆弧半径
4 逃逸曲线中分形自相似结构的讨论
4.1 逃逸曲线中的分形自相似结构
总结以上各种情况下的混沌逃逸曲线,奇异点较多的黑色区域和对入射条件的微小改变不敏感的白色区域相互交错,形成一类复杂的曲线,这样的体系显示出混沌动力学的标志——分形结构[3].当然该混沌系统中可能存在“黑带”自相似的分形结构[14,15],也就是说在不同的放大级别上,逃逸曲线的黑白区域分布是相似的[16].
回到原始参数下RIKEN器件中粒子逃逸曲线中来:由于该逃逸曲线为非对称结构,无法从中央区域逐级放大来寻找其自相似结构,所以我们采用将曲线中的混沌区域逐段放大的方法来寻找.图11为混沌区域存在的分形自相似结构,可以看到各级放大之后的图形与上一级图形在黑白区域的分布上是一致的,各级图形之间有着很好的相似度.
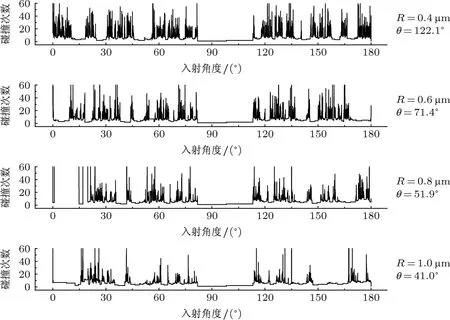
图10 R>0.35µm时圆弧半径对逃逸前碰撞次数的影响,右侧数据为对应的圆弧半径及圆心角角度

图11 原RIKEN器件中混沌区域的分形自相似结构 自上而下各级图形的取值范围分别为(49.8°,62.2°),(51.9°,54.6°),(52.35°,52.95°),(52.449°,52.579°),(52.4694°,52.4977°),(52.47395°,52.48003°);右侧数据为放大级数
4.2 自相似区域的讨论
我们把自相似区域的位置用圆(或者椭圆)逐级别标示出来,以探讨各放大级的位置与分形自相似性的关系.圆的直径(或者椭圆的长轴)Di为图11自相似结构中对应的第i条曲线的入射角范围,得到如图12(a)所示的嵌套圆结构,我们将之称为“眼式结构”,该结构也是自相似结构,放大后的局部与整体是相似的.图中的横轴为各级自相似图形的入射角度;由于圆(或者椭圆)表示的是一维长度量,因此不需要考虑图像纵坐标的标度.自相似放大区域占各级图形的比例较低(约占22%),从第三层圆开始其位置已无法仔细分辨.
为使图形易于观察,在图12(a)的基础上将圆的直径各级放大(圆心位置不变)得到新的结构D′i=Di×ai-1(4.6≥ a≥1).图 12(b)为 a=3时的“眼式结构”,图中的1,2两个圆已经相交,第2层及以后的圆仍为嵌套关系,由此说明图12(a)中1,2两层的自相似性并不好.结合图11的自相似图形可以发现,其中的前两个图形黑白区域分布有较明显差异,而其他图形之间无明显差异.由此得到结论:逃逸曲线的分形自相似结构中,各级放大区域在位置标度上也是自相似的,其相似度的好坏与逃逸曲线的相似性一致,各级放大区域在位置标度上的相似度越好逃逸曲线的自相似性越好.
统计图11中各级放大区域以及相邻放大区域间的比值(简称相似比),得到表1.表中给出了各级相似结构的放大区域以及相邻√放大级之间的相似比比值.利用标准差公式算得表1中相似比的标准差为0.0062,因此可以认为相邻放大区域间的比值是基本相等的.由此得到结论:分形自相似结构中,相邻放大级之间的相似比基本一致,在本结构中为21.71%.此方法可以用来检验自相似结构中放大级是否存在缺失,对于放大级的准确寻找具有一定的意义.

图12 (a)原始尺度的“眼式结构”;(b)a=3时的“眼式结构”

表1 各放大级区域及相邻放大级之间的比值
5 逃逸曲线的分形维数及讨论
分形几何与混沌动力学具有密切的联系,前文得到的混沌逃逸曲线需要分形几何来描述.分形维数是衡量一个体系混沌性质的重要参量,可以定量描述混沌性质的强弱.对于不规则形状的曲线一般采用盒计数法来计算其分形维数,将混沌逃逸曲线入射角平均细分为ε份,找出混沌区域所占的份数N(ε),则分形维数在包含混沌区域的N(ε)个盒子中,会出现全部混沌区域或者部分混沌区域两种情况,当ε改变时N(ε)也随之改变,因此计算得到的分形维数Df是变化的.从长远角度考虑,ε越大N(ε)中全部混沌区域所占的比例也就越多,当ε→∞时所有N(ε)个盒子均为全部混沌区域,体系的分形维数Df趋于稳定值[17].

图13 采用盒计数法计算原器件的分形维数
图13 为采用盒计数法算得的原器件的分形维数,逐步增大盒子的数量ε,曲线趋于稳定的斜率k=0.734即为体系的分形维数Df.由于盒计数法中的混沌盒子数量N(ε)不会超过盒子的总数量ε,所以采用这种方法计算得到的分形维数Df≤1.采用该方法计算其他参数下器件中粒子逃逸曲线的分形维数,进而可以得到分形维数与器件开口、腔长、圆弧半径等的关系曲线,如图14所示.
图14(a)中开口宽度d→0时分形维数下降非常快,这主要是由于开口宽度很小时,粒子在各角度入射时均难以逃逸,碰撞次数奇变少所导致.由于开口很小时粒子无法入射和逃逸器件腔,所以此段曲线在实际应用中可以忽略.此后随着开口宽度的增加体系混沌性减弱,分形维数Df逐渐降低趋向于0.图14(b)中腔长的增加使粒子的混沌性增强,分形维数Df逐渐增加趋向于1.图14(c)中在R=(0,0.20)区间分形维数随圆弧半径增加(弧度不变)而增加,这主要是圆弧的放大作用增强所导致.在R=(0.20,0.35)区间,器件拐角区域合并导致混沌性减弱,而圆弧半径增加导致混沌性增强,在二者共同影响下分形维数并没有明显增加.图14(d)中圆弧半径增加(弧度减小)导致其放大作用下降以及混沌性减弱,分形维数随之减小.可以看到不同器件参数下的分形维数变化情况与第3节中讨论的逃逸曲线的混沌性质是一致的.
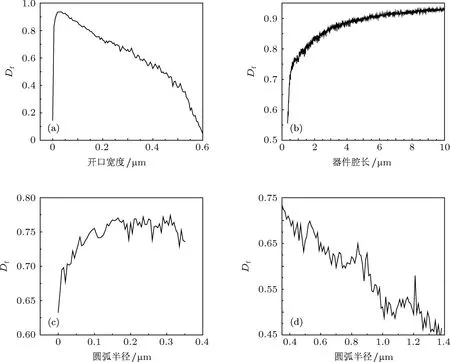
图14 分形维数与器件参数的关系曲线
6 结论
1)RIKEN器件的开口宽度、腔长、圆弧、拐角等均会影响粒子逃逸曲线的混沌性质,圆弧区域(主要是弧度)对混沌性质的影响比直线区域更显著,器件拐角的数量及距离都会对混沌性质产生影响.
2)通过对器件参数的控制改变器件的混沌性,对器件中粒子输运过程的稳定性控制有一定意义.
3)采用逃逸曲线定性比较和分形维数定量计算两种方法均可以描述体系的混沌性质,两种方法得到的混沌性质变化规律是一致的.
4)在RIKEN器件的粒子逃逸曲线中发现了很好的分形自相似结构,首次运用“眼式结构”分析法及相似比比较的方法对自相似结构进行了验证,得到了自相似结构与其位置和相似比的关联性.
[1]Hu G 1994 Random Force and Nonlinear Systems(Shanghai:Shanghai Technology and Education Press)p114(in Chinese)[胡岗 1994 随机力与非线性系统(上海:上海科技教育出版社)第114页]
[2]Zhong Y X 2010 Discussion on Chaos and Fractals(Beijing:Peking University Press)p5(in Chinese)[钟云霄2010混沌与分形浅谈(北京:北京大学出版社)第5页]
[3]Hansen P,Mitchell K A,Delos JB 2006 Phys.Rev.E 73 066226
[4]Ree S,Reichl L E 2002 Phys.Rev.E 65 055205
[5]Micolich A P,Taylor RP,Newbury R,Fromhold T M,Tench CR 2000 Europhys.Lett.49 417
[6]Jiang GH,Zhang Y H,Cai X J,Yang QN 2011 Shandong Science24 22(in Chinese)[蒋国辉,张延惠,蔡祥吉,杨秦男2011山东科学24 22]
[7]Micolich A P 2000 Ph.D.Dissertation(Australia:The University of New South Wales)
[8]Fromhold TM,Tench CR,Taylor RP,Micolich A P,Newbury R 1998 Physica B 249 334
[9]Zhao H J,Du M L 2007 Acta Phys.Sin.56 3827(in Chinese)[赵海军,杜孟利2007物理学报56 3827]
[10]Zhao H J,Du M L 2007 Phys.Rev.E 76 027201
[11]Song X F,Du M L,Zhao H J 2012 Sci.Sin.Phys.Mech.Astron.42 127(in Chinese)[宋新芳,杜孟利,赵海军2012中国科学:物理学力学 天文学42 127]
[12]Xu X Y,Zhang Y H,Huang F Z,Lin SL,Du M L 2005 Acta Phys.Sin.54 4538(in Chinese)[徐学友,张延惠,黄发忠,林圣路,杜孟利2005物理学报54 4538]
[13]Jiang G H,Zhang Y H,Bian H T,Xu X Y 2011 Chin.Phys.Lett.28 120507
[14]Mitchell K A,Handley JP,Tighe B,Knudson SK,Delos JB 2003 Chaos13 880
[15]Mitchell K A,Handley JP,Knudson S K,Delos JB 2003 Chaos 13 892
[16]Huang R S 2000 Chaos and Its Application(Wuhan:Wuhan University Press)p179(in Chinese)[黄润生2000混沌及其应用(武汉:武汉大学出版社)第179页]
[17]Taylor RP,Micolich A P,Jonas D 1999 Nature 399 422
