基于自适应核学习相关向量机的乳腺X线图像微钙化点簇处理方法研究*
2013-09-27姚畅陈后金YangYongYi李艳凤韩振中张胜君
姚畅 陈后金 Yang Yong-Yi 李艳凤 韩振中 张胜君
1)(北京交通大学电子信息工程学院,北京 100044)
2)(Department of Electrical and Computer Engineering,Illinois Institute of Technology,Chicago IL 60616,USA)
(2012年12月1日收到;2013年1月29日收到修改稿)
1 引言
乳腺癌是妇女发病率和死亡率最高的恶性肿瘤之一,乳腺癌的早期发现和诊断是提高治愈率和降低死亡率的关键[1,2].目前,应用于乳腺癌诊断的检测方法有:X射线影像技术、计算机断层摄影术、光声成像、核磁共振成像、微波成像等技术[3-9].其中,乳腺X线影像技术被认为是最可靠和最有效的方法[9].放射科医师利用它可以发现乳腺癌触诊而不能发现的早期微小病灶——微钙化点.在乳腺X线图像中,微钙化点是以小亮点出现的钙沉淀.通常单个的微钙化点对于乳腺癌的检测没有太大的意义,聚合成簇出现的微钙化点才是早期乳腺癌的重要症兆(如图1所示).研究表明,30%—50%确诊的乳腺癌患者在早期的乳腺X线图像筛查中有微钙化点簇出现[10].因此,乳腺X线图像中微钙化点簇的分析处理对乳腺癌的早期防治具有非常重要的意义.
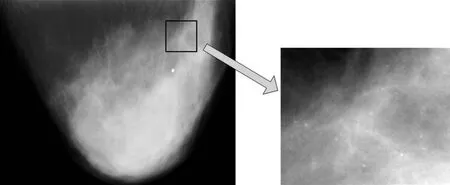
图1 乳腺X线图像(左)及其含有的一个微钙化点簇的放大图(右)
由于微钙化点在形状、大小、分布上都有很大变化性,且其灰度与周围乳腺组织灰度接近,所以微钙化点的检测比较困难.目前,关于微钙化点的检测方法已有不少文献报道,主要可分为:图像增强方法、随机建模方法、多尺度分解方法和机器学习方法[8-13].其中,基于机器学习的微钙化点检测方法能获得较好的微钙化点检测性能,是当前微钙化点簇处理方法研究的主要方向.Naqa等[12]将支持向量机(support vector machine,SVM)应用于微钙化点检测,采用连续增强学习方法训练分类器以进一步提高预测能力,实验结果证明了支持向量机方法的检测性能要优于神经网络方法、图像差分方法和小波多尺度分解方法.Wei等[13]将相关向量机(relevance vector machine,RVM)应用于微钙化点簇处理,通过实验仿真证明了RVM在获得与SVM相同的性能情况下,分类器的计算复杂度较SVM大幅下降,有利于临床应用.但是,由于RVM最终获得的相关向量全部来自训练集中的训练样本,且模型采用的核函数的参数只能通过对训练集样本采用交叉验证方法来人工设定,从而导致RVM算法性能的进一步提高受到了影响.
2009年Tzikas等[14]提出了一种基于增量学习的稀疏贝叶斯建模方法,即自适应核学习相关向量机(adaptive kernel learning based relevance vector machine,ARVM)方法.在原理上,ARVM与RVM相似.然而,在RVM方法中,相关向量来自训练集中的训练样本,且模型采用的核函数的参数只能通过对训练集采用交叉验证方法来确定.而在ARVM方法中,核函数参数由模型在训练时自动优化设置,模型核函数允许同时采用不同类型的基函数构成,更适应数据的局部特征.为避免过拟合,模型采用了一种稀疏度先验方法控制模型有效参数的个数,从而使得模型比RVM更稀疏.
基于此,本文尝试性地采用ARVM用于乳腺X线图像微钙化点簇分析,研究了基于ARVM的乳腺X线图像微钙化点簇处理方法.该方法首先将微钙化点检测看作一个二分类的监督学习问题,运用ARVM作为分类器判断图像中每一个位置是否为微钙化点;然后采用形态学处理去除干扰噪声并对判别出的微钙化点进行分簇.此外,为提高算法的运算速度,实现了一种基于图像分块并行运算的ARVM微钙化点簇快速处理方法.
2 ARVM理论
ARVM是在RVM的基础上提出的一种核函数参数自适应学习的稀疏贝叶斯建模方法.相比较于RVM,其最大的特点是模型核函数参数在训练时自动优化设置,且模型核函数允许同时采用不同类型的基函数构成.同时,模型采用稀疏度先验方法控制模型有效参数的个数,从而使得模型比RVM更稀疏.基于这些特性,ARVM能很好地解决回归和分类问题.本文采用ARVM来解决二分类问题.
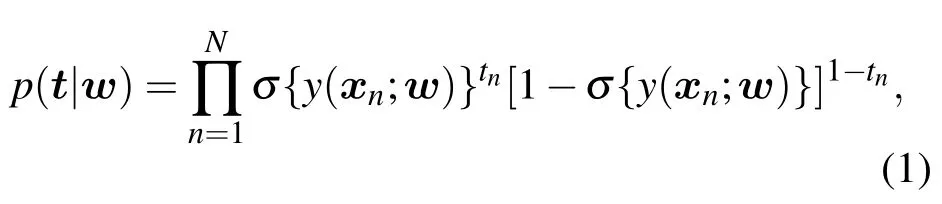
其中
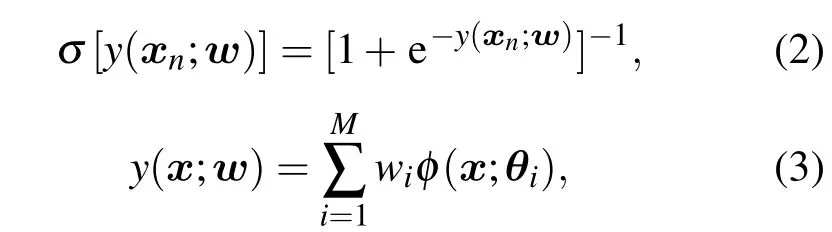
w=(w1,w2,···,wM)T为模型的权值,φ(x;θi),(i=1,···,M)是参数为 θ =(θ1,θ2,···,θM)T的核基函数集.
对于模型权值w的分布,采用不同精度的高斯先验αi进行控制,
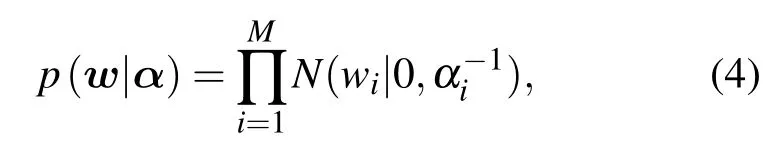
其中 α =(α1,···,αM)T.
对于模型每个噪声εn,则为具有不同精度βn的高斯噪声:
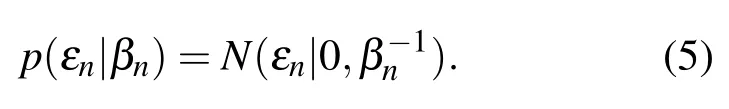
利用贝叶斯定理,权值的后验分布概率为
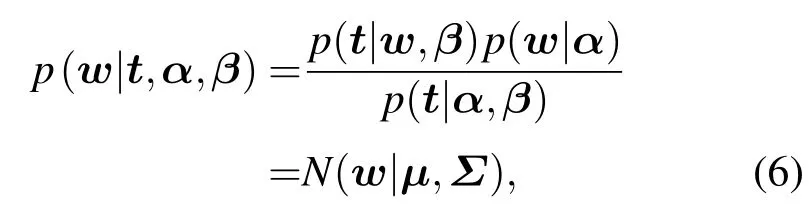
在该算法中,尽管α和β被引入先验分布,但是并不计算这些隐藏变量的联合后验概率而是只计算权值后验概率p(w|t,α,β),接着计算出后验概率 p(α,β|t)∝p(t|α,β)p(α,β)最大值时的 α 和 β 的最大后验概率(maximum a posteriori,MAP).由于假设α和β的无信息先验,∫更新公式可以通过最大化边缘似然率 p(t|α,β)= p(t|w,β)p(w|α)d w 获得.
为了避免过拟合,不同于RVM采用伽玛(Gamma)先验分布的方法,ARVM对于α引入超先验用来直接控制模型有效参数的个数:

其中,S=ΦΣΦTB称为平滑矩阵,矩阵的迹trace(S)称为S的自由度,表示模型参数的有效个数,c为稀疏度参数,控制模型期望稀疏度的大小.计算trace(S)得:
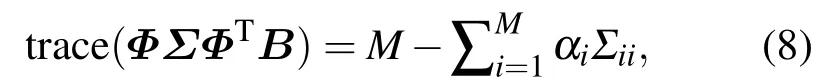
因此,稀疏度先验式(7)可写为
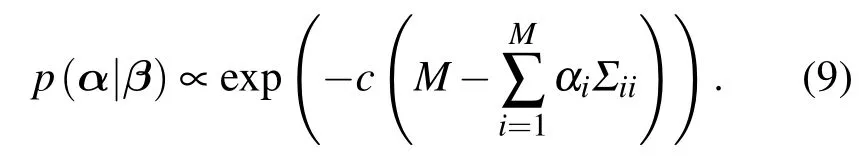
基于超先验p(α|β),模型超参数α和β通过最大化后验概率 p(α,β|t)∝ p(t|α,β)p(α|β)p(β)进行更新.由于协方差Σ的计算复杂度为O(N3),算法采用增量方法[15]进行学习.初始假设所有αi=∞,即假设所有基函数由于稀疏度控制为空,然后进行迭代更新,并判断每次迭代得到的基函数是否满足条件添加到模型或是否需要从模型删除.当有基函数添加到模型后,相应的参数αi设定为使后验概率最大时的值.
在增量方法中,对数化的后验概率L中仅与参数αi相关的项为
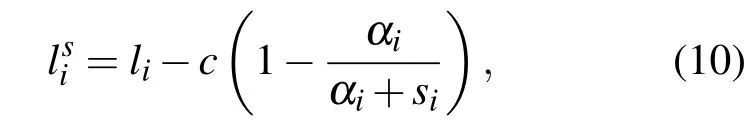
lis的梯度为
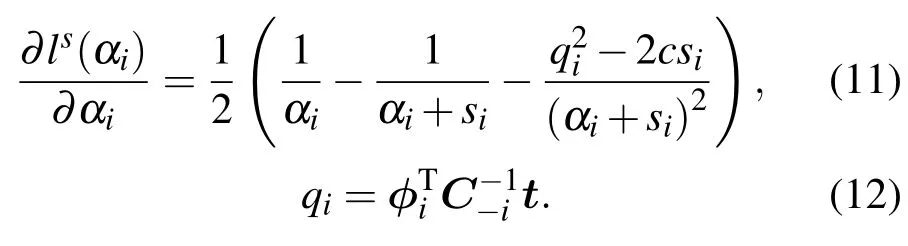
将梯度取零,从而求得lis取最大值时的αi为

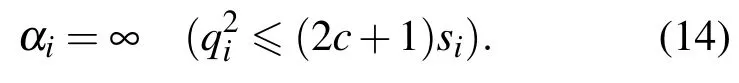
同样,对于超参数β的更新,也是取后验概率L对β求偏导后等于零的数值解.此外,对于模型核基函数φ(x;θi)中的不同核函数参数θi,算法通过计算后验概率L对基函数参数θ的偏导,然后采用拟牛顿法(Broyden Fletcher Goldfarb Shanno,BFGS)求解最优值.
3 基于ARVM的微钙化点簇处理
本文将乳腺X线图像中的微钙化点检测问题看作一个二分类问题,采用ARVM算法实现对微钙化点簇的处理.具体来说,包括微钙化点检测和微钙化点分簇两步操作.其中,微钙化点检测通过对预处理后的乳腺X线图像逐个提取像素点位置的图像特征,然后采用训练好的ARVM分类器判断其是否属于“微钙化点”类或“非微钙化点”类来实现;微钙化点分簇则是通过对检测出的微钙化点采用Kallergi标准来判断实现.
3.1 图像预处理
微钙化点通常与背景中的乳腺组织重叠,且其灰度与周围乳腺组织灰度接近,必须进行预处理抑制背景噪声、增强对比度.本文采用文献[13]的高通滤波方法进行预处理.通过大量实验,高通滤波器设计为截止频率ωc=0.125、长度为41的一维有限脉冲响应滤波器,然后采用基于麦克莱伦(McClellan)矩阵的频率变换将其转换为二维有限脉冲响应滤波器,如图2所示.为降低各图像灰度差异,滤波后的图像进行了归一化处理.图3所示为高通滤波后的图像.
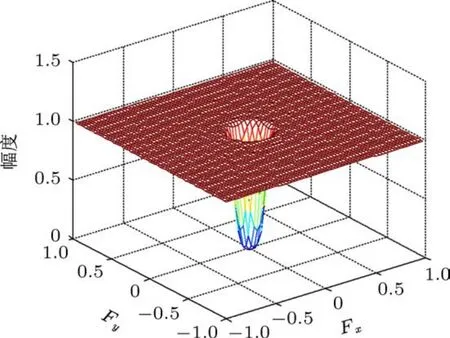
图2 高通滤波器

图3 高通滤波后的结果
在ARVM的训练中,作为金标准的数据为专家手工标定的每个微钙化点的中心位置.由于专家手工标定的微钙化点中心不一定在微钙化点亮度最亮的位置,为减少算法通过计算机找出的微钙化点中心与专家标定的中心位置的误差,我们采用线性滤波的方法校正专家手工标定的中心位置.首先设计一个大小为7×7的加权平均滤波器掩模,如图4(a)所示;然后,对归一化的图像中专家标识的微钙化点中心位置的15×15邻域图像进行形态学线性滤波,找出滤波后结果中的最大峰值点,将该点位置标记为校正后的微钙化点中心,校正过程如图4(b)所示.
3.2 特征提取
特征提取是微钙化点检测的关键步骤,特征提取的结果直接影响到分类器的检测性能.由于微钙化点在乳腺X线图像中具有较好的定位性,因此,判断图像中一个像素点位置是否是微钙化点时,可以通过提取其周围邻域内的图像内容进行判别.本文提取乳腺X线图像中待判别像素点位置的G×G邻域像素构成特征向量,作为ARVM的输入,待判别的像素点位置位于G×G窗的中心.具体来说是将每个G行G列(G×G)的图像窗排列为一个G×G维的行向量.其中,G的选择条件为:窗口的大小能覆盖整个微钙化点像素区域同时又不与邻近的微钙化点区域有重叠.本文采用的图像数据库中,乳腺X线图像的精度为0.05 mm/pixel,通过实验,G取经验值15最为合适.图5所示为预处理后的乳腺X线图像中提取出的含有微钙化点的特征样本.
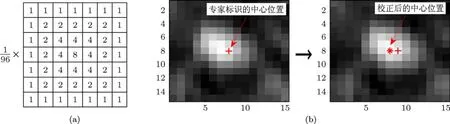
图4 中心位置校正 (a)滤波器掩模;(b)中心位置校正过程

图5 提取的含有微钙化点的样本
3.3 模型核函数和稀疏度
ARVM的最重要特性是模型在训练期间能自动优化设置核函数的参数.本文实验中主要考虑常用的多项式核函数(polynomial kernel,简记为Poly)和高斯径向基核函数(Gaussian RBF kernel,RBF).由于核参数的自适应连续优化是基于核参数的偏导进行的,因此,需要计算核函数对其参数的偏导.
1)多项式核函数

其中d为阶数,d>0,mi为模型训练过程中需要自动优化的核参数.核函数对mi求偏导:
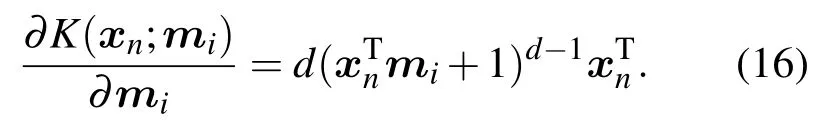
2)高斯径向基核函数

其中,均值向量mi和方差hi为模型训练过程中需要自动优化设置的核参数.核函数分别对mi和hi求偏导:

核函数参数mi的初始值为随机挑选的训练样本,然后通过拟牛顿法迭代优化,算法最终收敛获得的mi即为模型的相关向量.
模型的复杂度采用(7)式的稀疏度先验方法进行控制,其中稀疏度参数c根据如下常用标准取值[14]:

3.4 微钙化点分簇
通过ARVM分类器检测出来的微钙化点进行后续分簇操作时,由于有些检测出来的相互邻近的像素点可能是同一个微钙化点的一部分,因此需要将这些像素点合并到同一个微钙化点.本文采用形态学方法进行处理,同时将结果中孤立的可疑像素点去除.
形态学处理后的微钙化点采用Kallergi标准[16]划分为不同的微钙化点簇.该标准将检测出的微钙化点判别为一个真阳性(true positive,TP)簇时需要同时满足以下两个条件:
1)相互邻近的目标的近邻距离小于0.4 cm;
2)在面积为1 cm2的范围内检测出的微钙化点中应至少包含有3个真正的微钙化点.
当一组检测出的微钙化点满足簇判别条件1),但不包含真正的微钙化点时,该簇称为假阳性(false positive,FP)簇.
4 微钙化点簇处理方法的快速实现
训练好的分类器对测试图像进行微钙化点检测时,将15×15的窗口在图像上滑动以提取每个像素点的特征向量进行判断.将提取的特征向量排列为特征矩阵,然后采用分类器进行判别,判别结果再排列回原图像位置,这样可以节省大量的计算机运行时间.但由于图像和特征向量太大,从而使得特征矩阵也变大,算法进行矩阵处理时由于运算量太大导致对机器内存要求变高,进而使得算法执行速度下降.为此,本文提出一种图像分块的处理方法.该方法将预处理后的待检测乳腺图像划分为J×J块子图像;然后分别提取每个子块中各像素点的特征向量,即提取每一个像素点的15×15邻域并排列成225维的行向量,将子块中各特征向量依次排列为待识别的特征向量矩阵,交由训练好的ARVM分类器进行判断,这一步操作也可以通过计算机并行运算快速实现;最后,将J×J块子图像的判断结果合并为整幅图像的识别结果.分块方法在提高算法的执行速度的同时不改变算法的检测结果.图6所示为J取4时的图像分块检测方法示意图.
将图像分块和ARVM应用于乳腺X线图像微钙化点簇处理,本文方法流程如下:
步骤1 利用训练样本集训练ARVM.
1)读入训练乳腺图像,进行高通滤波和归一化预处理;
2)对预处理后的图像校正专家手工标定的微钙化点中心坐标;
3)对中心坐标校正后的图像提取训练样本特征向量,并将其排列为训练样本特征矩阵;
4)利用获得的训练样本特征矩阵训练ARVM.

图6 图像分块方法示意图
步骤2 利用训练好的ARVM识别测试图像中的微钙化点.
1)读入待测试乳腺图像,进行高通滤波和归一化预处理;
2)对预处理后的图像采用分块方法将图像分为J×J个子块图像;
3)依序每次对其中一个子块图像提取其待测试特征向量,并将其排列为待测特征矩阵;
4)采用训练好的ARVM对待测试特征矩阵进行判断,获得识别的可疑微钙化点;
5)重复步骤2中第3),4)步,将获得的各子块图像检测结果合并为整幅图像的检测结果.
步骤3 对获得的可疑微钙化点识别结果进行形态学后处理,去掉干扰噪声.
步骤4 对微钙化点进行分簇,获得最终的微钙化点簇处理结果.
5 实验仿真及结果分析
实验采用美国芝加哥大学放射系临床采集的数据库[13]来检验算法的有效性.该数据库由66个临床病例共141幅图像组成,每幅图像包含有一个或多个后期经临床确诊的微钙化点簇.每幅图像的大小为3000×5000像素,图像分辨率为0.05 mm/pixel,10位灰度.同时,数据库提供了每幅图像经由一组有经验的放射科专家手工标定的微钙化点信息以及每幅图像中乳腺区域的二值掩模.为节省计算时间,与文献[13]方法一样,提取每幅图像中包含专家标定的微钙化点在内的800×800像素区域进行实验.
5.1 ARVM训练
实验将图像库随机分为两个独立的子集,每个子集包含33个病例.其中,来自同一个病例不同视角的乳腺X线图像属于同一个子集.将其中一个子集用于训练ARVM分类器(33个病例,71幅图像),另一个子集用于测试分类器(33个病例,70幅图像).这样,来自同一个病例的所有乳腺X线图像将要么只用于训练,要么只用于测试,不会同时用于模型的训练和测试.
训练图像集包含的乳腺X线图像中总共有1578个微钙化点.对于每个微钙化点,提取其中心位置的15×15邻域窗,并将窗内所有像素点值排列为一个1行225列的行向量,表示为xi.xi即为训练样本中类别标签为“微钙化点出现”(ti=+1)的正样本.总共提取有1578个正样本.同样地,提取2倍于有微钙化点出现样本数的背景像素窗排列为“无微钙化点出现”(ti=-1)的负样本(3422个).无微钙化点出现的负样本是从训练集图像的背景中随机提取,且不与其他任意样本窗有重叠.图7所示为从训练集提取的部分训练样本.
提取完训练样本集后,需要确定ARVM所采用的核函数类型以及模型稀疏度参数c的取值才能对分类器进行训练.本实验采用5折交叉验证(5-fold crossvalidation)方法来确定.
交叉验证[17]是一种统计学上将数据样本切割成较小子集,先在部分子集上做分析,而后在其他子集上对此分析进行确认及验证的实用方法.本文采用的5折交叉验证方法为:
1)将训练样本随机分为5个同样大小的子集;
2)对于要设置的参数,从5个子集中选择1个子集保留作为测试集,其余4个子集作为训练集训练模型;模型训练好后用保留的测试集进行验证,获得该次的测试结果;

图7 提取的训练样本 (a)“微钙化点出现”样本;(b)“无微钙化点出现”样本
3)交叉重复5次,每个子集被验证1次,平均5次的测试结果作为该参数值的泛化误差.
改变参数的取值,5折交叉验证方法将获得相应的泛化误差,选择最小泛化误差对应的取值作为该参数的设定值.
表1给出了不同核函数类型和不同稀疏度值时模型的泛化误差,其中Poly1,Poly2,Poly3,Poly4分别表示1,2,3,4阶的多项式核函数;RBF表示高斯径向基核函数.从表1可以看出,最小的泛化误差为0.0385,其对应的核函数为2阶多项式核函数,稀疏度参数为lg(N)/2.因此,ARVM中的核函数采用2阶多项式核函数、稀疏度参数c=lg(N)/2.

表1 不同参数值的ARVM获得的泛化误差
采用训练样本集对ARVM进行训练,直到算法收敛,从而获得训练好的分类器.本实验中当连续10次迭代每次模型后验概率L的增量可忽略且模型权值非零个数恒定不变时,认为分类器已经训练好.图8所示为本实验采用2阶多项式核函数的ARVM收敛过程,由图8可以看出,算法在迭代到第5次时就已经训练好了分类器,训练好的分类器相关向量个数为5,且这些相关向量不是直接来自训练样本集,而是模型通过增量方法自适应优化获得,相关向量如图9所示.
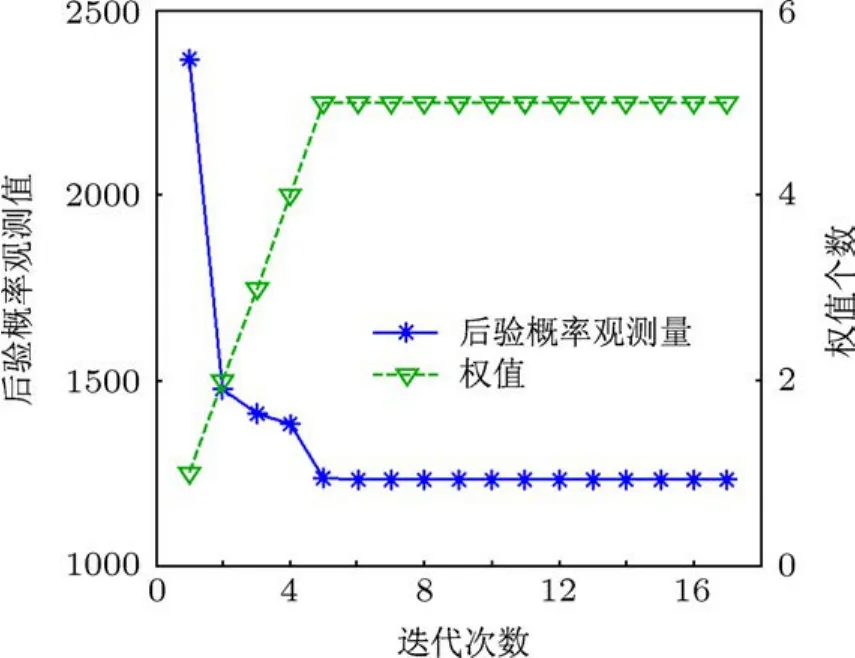
图8 ARVM收敛过程

图9 相关向量
5.2 处理结果及算法性能评价
图10 所示为本文算法对图1中局部放大图的微钙化点检测结果,其中“°”表示放射科专家标出的真实微钙化点位置,“+”表示本文算法检测出的微钙化点.对图10结果进行分析可知,尽管本文算法漏检了两个真实微钙化点,且多检出了两个假阳性微钙化点,但是整个检测出的微钙化点目标满足Kallergi微钙化点簇判别标准,因此成功地检测出了该微钙化点簇.
为比较算法性能,实验同时将文献[13]中的RVM算法采用相同的测试集进行比较.实验结果采用自由响应受试者工作特征(free-response re-ceiver operating characteristic,FROC)[18]曲线进行分析和评价.FROC曲线通过计算真阳性簇的正确率(也叫真阳性率)和平均每幅图像的假阳性簇个数,并将不同阈值下这两个检测量的统计值绘制在同一个图中来评价算法性能.曲线越接近图的左上角,说明算法对微钙化点簇的处理性能越好.实验通过改变判别微钙化点的阈值来绘制算法处理结果的FROC曲线.图11所示为近邻距离Dnn=0.4 cm时,本算法ARVM和文献[13]的RVM算法对微钙化点簇处理结果的FROC曲线图.

图10 检测出的微钙化点,“○”表示专家标出的真实微钙化点,“+”表示本文算法检测出的微钙化点
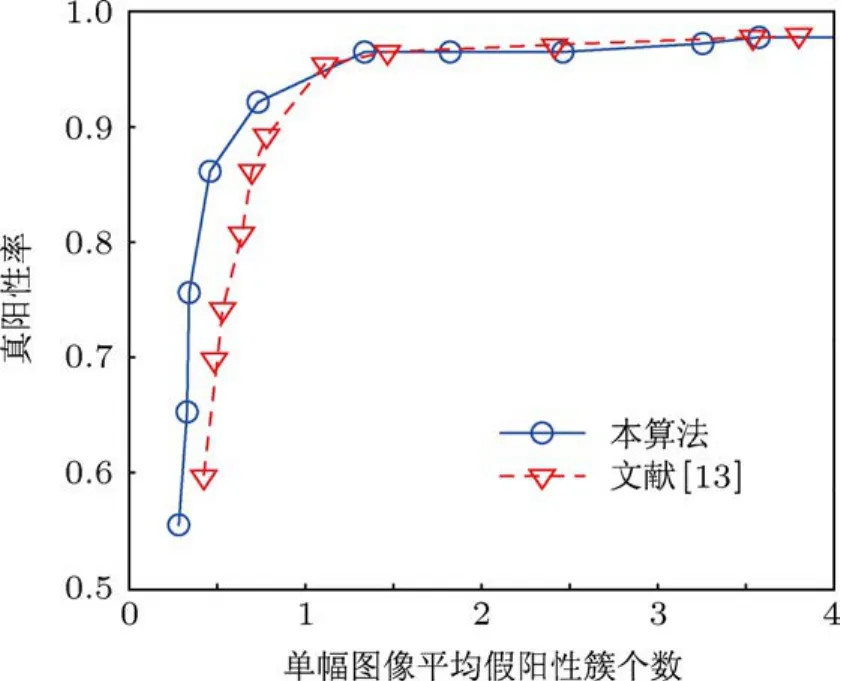
图11 D nn=0.4 cm时的FROC曲线
由图11可以看出,当单幅图像平均假阳性簇个数在[0,1]区间时,本文ARVM算法的真阳性率要高于文献[13]的RVM算法;单幅图像平均假阳性簇个数在[1,4]区间时,ARVM与RVM的真阳性率接近.临床采用计算机辅助诊断系统提供辅助信息时,检测出的每幅图像平均假阳性簇个数如果太高则对辅助诊断意义不大,医生主要关注每幅图像平均假阳性簇个数小于1时的真阳性簇检测结果.本文实现的ARVM算法正是在这个区间算法性能要优于RVM算法.特别是当单幅图像平均假阳性簇个数为0.5时,ARVM算法的真阳性率为87%,而RVM算法的真阳性率只有71%.
由于FROC曲线受微钙化点簇的判别标准影响,因此,在本文实验中,改变微钙化点簇的判别标准,即改变近邻距离Dnn,然后统计相应的FROC曲线值来观察算法的性能.图12和图13所示分别为Dnn=0.3 cm和Dnn=0.2 cm时的FROC曲线图.综合图11,12和13可以看出,当改变近邻距离,Dnn的取值从0.2 cm增大到0.4 cm时,ARVM和RVM算法对微钙化点簇的处理性能都在不断提高;但在相同的近邻距离情况下,当单幅图像平均假阳性簇个数小于1时,本文算法的处理性能都要优于RVM算法,即在相同的假阳性簇个数情况下,ARVM算法的真阳性率要高于RVM算法.
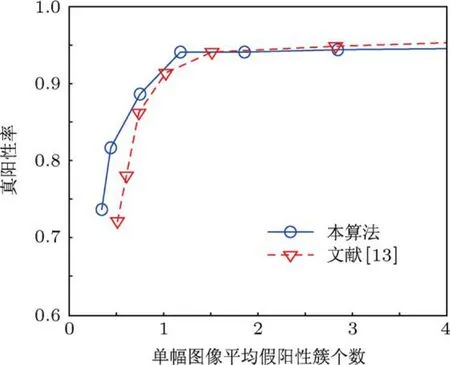
图12 D nn=0.3 cm时的FROC曲线
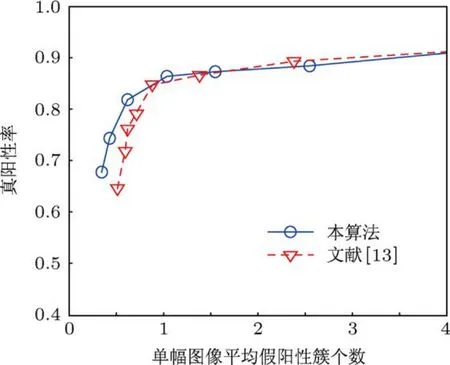
图13 D nn=0.2 cm时的FROC曲线
由于组织结构特性的差异,女性乳腺通常分为致密型乳腺和脂肪型乳腺.乳腺腺体类型的不同,导致算法对其X线图像中的微钙化点簇的处理难度也不同.通常,致密型乳腺X线图像比脂肪型乳腺X线图像背景更复杂,对比度更低,处理也更难.实验为降低测试图像集中不同类型病例分布对算法性能的影响,采用自助重采样(bootstrapping)方法[19,20]进行2000次测试检验算法的鲁棒性,具体执行步骤为:
1)从测试图像集(70幅图像)中随机提取30幅图像作为该次测试的测试图像子集;
2)对30幅图像子集采用训练好的分类器进行测试,并画出该次测试结果的FROC曲线;
3)重复步骤1)和2),进行2000次测试;
4)画出分类器测试结果的平均FROC曲线.
图14所示为本算法对2000个通过自助重采样获得的测试图像子集处理结果的FROC曲线图.其中,每一条蓝色曲线表示算法对1个测试图像子集处理获得的FROC曲线,共2000条;中间曲线表示2000次测试结果的平均FROC曲线,曲线上每个操作点的数据条表示在当前平均每幅图像检测到的假阳性微钙化点簇的情况下,算法对不同组合测试图像子集处理获得的微钙化点簇真阳性率的波动情况,数据条长度表示真阳性率的标准方差大小.数据条越短,波动性越小,鲁棒性越强.
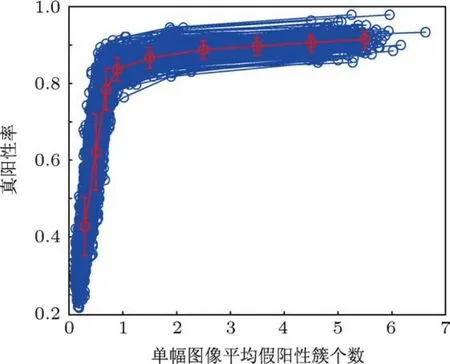
图14 本算法2000次自助重采样测试的FROC曲线图
实验对本文ARVM算法和文献[13]的RVM算法在不同近邻距离下进行自助重采样测试,并对获得的平均FROC曲线进行比较.图15,16和17所示分别为Dnn=0.2,0.3和0.4 cm时2000次自助重采样测试获得的平均FROC曲线图.

图15 D nn=0.2 cm时2000次自助重采样测试结果

图16 D nn=0.3 cm时2000次自助重采样测试结果
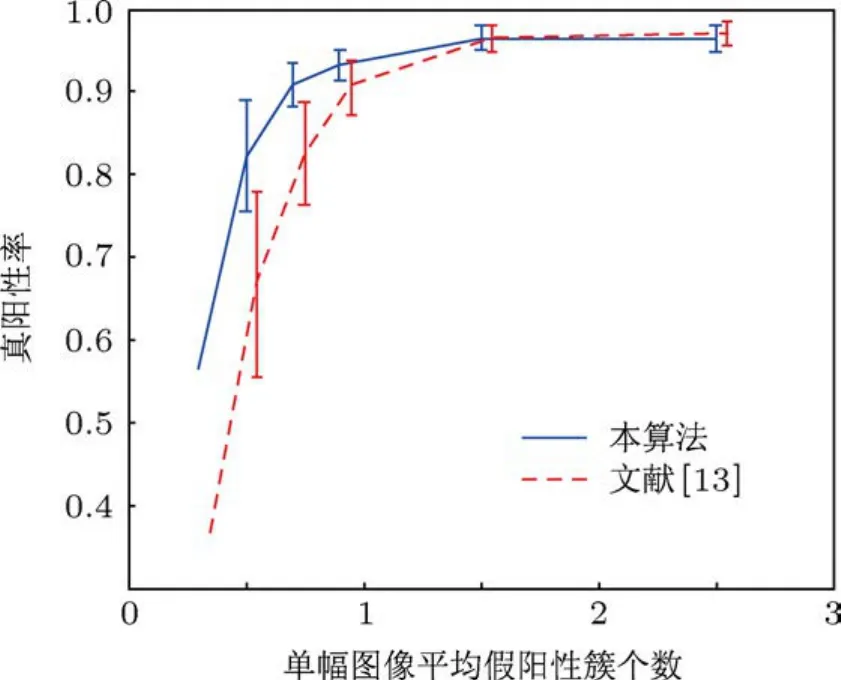
图17 D nn=0.4 cm时2000次自助重采样测试结果
从图15,16和17可以看出,不论在哪种近邻距离情况下,当单幅图像平均假阳性簇个数小于1.5时,ARVM算法获得的真阳性率总要高于RVM算法;同时从数据条的长度可以看出,对于不同组合类型的测试图像集,ARVM算法真阳性率的波动性要比RVM算法小,具有更强的鲁棒性.
5.3 算法运行效率和稀疏性比较
图像分块大小J的取值一方面与测试图像的大小有关,另一方面与实验机器配置有关,并不是J取值越大,算法效率越高.本实验在双核、主频为1.60 GHz,内存为1 G的台式计算机Matlab R2010a平台上进行,测试图像区域大小为800×800像素.图18所示为J不同取值情况下ARVM检测完一幅图像的时间.由图18可见,J取值为200时能获得最快的检测速度.

图18 J不同取值情况下ARVM测试时间统计图

表2 算法执行时间和相关向量数
为比较算法的计算复杂度和运行效率,本算法ARVM和文献[13]中RVM的运行时间和模型相关向量个数如表2所示.其中,训练时间指在训练阶段交叉验证方法中平均每次的训练时间,测试时间指在测试阶段训练好的分类器对每幅乳腺X线图像的平均测试时间.从表2可以看出,相关向量个数由RVM的72个降到了ARVM的5个,相关向量个数的减少意味着获得的分类器越稀疏,从而使得模型测试时的计算复杂度越低,计算速度越快.这可从分类器的测试时间体现出来,当对整幅图像逐个像素点遍历检测时,RVM的测试时间为129.8 s,而ARVM的测试时间为80.4 s;当采用图像分块方法检测时,RVM的测试时间为62.5 s,而ARVM的测试时间缩短为24.1 s.此外,从表2还可以看出,ARVM的训练时间长于RVM,这是因为ARVM算法自动优化模型参数时要花费更多的时间.由于模型通常在用于测试前提前训练好,因此训练时间对于模型的临床应用影响不大.
6 结论
利用自适应核学习相关向量机具有模型核参数自动优化设置、核基函数类型可以任意组合以及模型更稀疏的特性,本文将自适应核学习相关向量机应用于微钙化点簇处理,研究了基于自适应核学习相关向量机的乳腺X线图像微钙化点簇处理方法,同时为提高模型的运算速度,实现了一种基于图像分块的自适应核学习相关向量机的微钙化点簇快速处理方法.通过实验仿真和算法性能分析,结果表明基于自适应核学习相关向量机的微钙化点簇处理方法在较低的单幅图像平均假阳性簇个数时能获得比相关向量机方法更好的处理性能,模型更稀疏,同时实现的快速方法能进一步降低微钙化点簇的处理时间,有利于临床应用.
[1]Ahmed M H,Magda E 2011 IEEE Reviws in Biomedical Engineering 4 103
[2]Zhang X S,Gao X B,Wang Y,Zhang SJ2010 J.Infrared Millim Waves 29 27(in Chinese)[张新生,高新波,王颖,张士杰2010红外与毫米波学报29 27]
[3]Liu G D,Zhang Y R 2011 Acta Phys.Sin.60 074303(in Chinese)[刘广东,张业荣2011物理学报60 074303]
[4]Xiang L Z,Xing D,Guo H,Yang SH 2009 Acta Phys.Sin.58 4610(in Chinese)[向良忠,邢达,郭华,杨思华2009物理学报58 4610]
[5]Zhang H 2004 Acta Phys.Sin.53 2515(in Chinese)[张航2004物理学报53 2515]
[6]Xu X H,Li H 2008 Acta Phys.Sin.57 4623(in Chinese)[徐晓辉,李晖2008物理学报57 4623]
[7]Xiao X,Xu L,Liu B Y 2013 Acta Phys.Sin.62 044105(in Chinese)[肖夏,徐立,刘冰雨2013物理学报62 044105]
[8]Che L L,Zhang G Y,Song L,Cao W F 2011 Chin.J.Med.Phys.28 2467(in Chinese)[车琳琳,张光玉,宋莉,曹卫芳2011中国医学物理学杂志28 2467]
[9]Tang J,Rangayyan RM,Xu J,Naqa IEl,Yang Y Y 2009 IEEETrans.Inform.Technol.Biomed.13 236
[10]Jing H,Yang Y Y,Nishikawa RM 2011 Phys.Med.Biol.56 1
[11]Jiang J,Yao B,Wason A M 2007 Comput.Med.Imag.Graph.31 49
[12]Naqa IE,Yang Y Y,Wernick M N,Galatsanos N P,Nishikawa R M 2002 IEEETrans.Med.Imag.21 1552
[13]Wei L,Yang Y Y,Nishikawa R M,Wernick M N,Edwards A 2005 IEEETrans.Med.Imag.24 1278
[14]Tzikas D G,Likas A C,Galatsanos N P 2009 IEEE Trans.Neural Networks20 926
[15]Tipping M,Faul A 2003 Proceedingsof the Ninth International Workshop on Artificial Intelligence and Statistics Key West,USA,January 3—6,2003 p1
[16]Kallergi M,Carney GM,Gaviria J1999 Med.Phys.26 267
[17]Muller K R,Mika S,Ratsch G,Tsuda K,Scholkopf B 2001 IEEE Trans.Neural Networks12 181
[18]Bunch PC,Hamilton JF,Sanderson GK,Simmons A H 1978 J.Appl.Photogr.Eng.4 166
[19]Samuelson FW,Petrick N 2006 Proceedingsof 3rd IEEEInternational Symposium On Biodedical Imaging Arlington,USA,April 4—6,2006 p1312
[20]Xing HY,Qi ZD,Xu W 2012 Acta Phys.Sin.61 240504(in Chinese)[行鸿彦,祁峥东,徐伟2012物理学报61 240504]
