基于二阶离散变分方法的非线性映射参数估计*
2013-09-27曹小群
曹小群
(国防科学技术大学计算机学院,长沙 410073)
(2012年11月11日收到;2012年12月27日收到修改稿)
1 引言
近年来混沌控制和同步已经成为非线性科学研究中的重要方向之一,在已知精确参数的前提下相应的理论和方法已经得到广泛发展[1-3].在实际中,由于混沌系统的复杂性,某些参数经常无法测量或确定;或者出于保密通信等特殊原因,系统的某些参数不可知.此时,要实现对混沌系统的控制或同步,上述方法有相当的局限性.因此参数估计是混沌控制与同步中首先必须解决的课题,具有重要的现实意义.文献[4]引入基于反馈的同步和自适应控制方法,对若干混沌系统进行了参数估计;文献[5]通过最小化平均同步误差,对一个给定的混沌动态系统进行了参数估计;文献[6]通过参数自适应方法对目标系统的参数进行估计,达到了广义同步的目的;文献[7]提出了未知参数辨识观测器的概念,并对Lorenz系统的参数进行了辨识;文献[8]提出了一种基于变分原理的混沌系统参数估计方法,并对Lorenz系统和超混沌Chen系统的参数进行了估计.近年来一系列智能优化算法已经成功应用于混沌系统参数估计中,如改进粒子群优化算法[9]、混沌蚂蚁群算法[10]、混合差分进化算法[11]和混合交叉进化算法[12]等.
非线性映射是混沌控制和同步领域中一类重要的混沌系统,其未知参数估计也是一个必须解决的关键问题.非线性映射参数估计是离散动力系统研究中典型的反问题,和正问题不同,它一般通过观测数据来反求系统的参数或初/边值.因为观测中不可避免地包含有噪声以及系统固有的非线性,所以反问题求解过程中经常出现不适定现象:解不一定存在、即使解存在也不惟一、在解存在惟一条件下也不稳定(即解不连续依赖于观测数据)[13,14].因此非线性映射系统参数估计问题的求解通常采用特殊方法[8-13].本文基于二阶离散变分原理[14-18]来估计非线性映射中的未知参数.首先引入拉格朗日乘子向量,将以非线性离散系统为约束的最优化问题转换为无约束最优化问题,并利用离散变分方法导出了伴随方程和目标泛函梯度表达式;其次采用二阶离散变分方法导出了二阶伴随方程和Hessian矩阵-向量乘积的通用公式;然后设计了二阶离散变分方法估计非线性映射中未知参数的算法流程,并以此估计了Hyperhen´on映射[19]和二维抛物映射[20]中的未知参数.仿真结果表明:该方法具有很高的估计精度,同时具有较好的抗噪声性能.
2 问题描述
考虑如下n维非线性映射系统的未知参数估计问题:
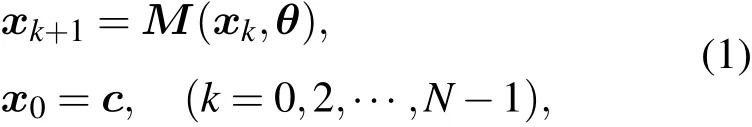
其中x0和xk∈Rn分别表示n维初值和状态向量,M(xk,θ):Rn×Rm→Rn表示非线性映射的模式函数向量,θ =(θ1,θ2,···,θm)T∈ Rm表示需要估计的未知物理参数向量.目标是利用非线性映射的观测数据准确辨识出不可测的未知参数向量θ,在观测噪声满足高斯分布的情况下,该问题可通过对下面具有最小二乘意义的目标泛函求极小值而解决:

其中yko和Rk(k=1,2,3,···,N)分别表示映射系统的观测向量和观测误差协方差矩阵,〈·,·〉表示欧氏空间的内积.显然,非线性映射的未知参数估计问题变成在离散状态方程(1)式约束下的目标泛函最优化问题.但是,由于非线性映射物理系统的强非线性和不稳定性将导致目标泛函J(θ)中可能存在多个局部极值点,从而使得仅仅依靠一阶导数(即目标泛函梯度 ∇θJ=(∇θ1J,∇θ2J,···,∇θmJ)T)信息很难准确估计未知参数值,进而使得如何精确计算目标泛函的高阶信息(例如,与Hessian矩阵有关的信息)就成为一个重要问题.同时考虑到未知参数向量θ是通过非线性映射系统与目标泛函间接相关的,因此要准确地得到J关于θ的二阶导数信息是非常困难的.本文利用二阶离散变分方法给出了切线性方程、二阶伴随方程和准确计算Hessian矩阵(∇θ2J)-向量乘积的公式,既可以避免Hessian矩阵直接求解的巨大计算代价,又可以加快最优化算法的收敛速度和提高未知参数的估计精度.
3 非线性映射参数估计的二阶变分方法
3.1 一阶变分方法
首先引入n维拉格朗日乘子向量λk∈Rn(k=0,1,2,···,N),将以非线性映射系统为约束条件的最优化问题(2)式转化为下面(3)式表示的无约束最优化问题:

Jk(θ)的一阶变分可由下面的表达式给出:
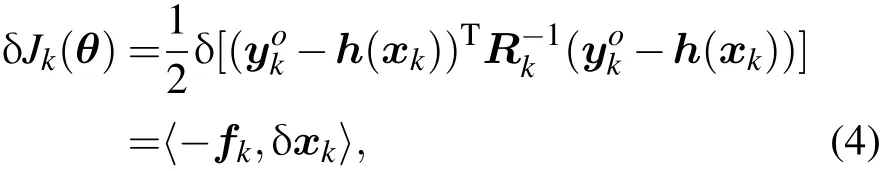
其中
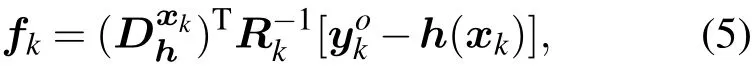

另外(3)式的一阶变分为
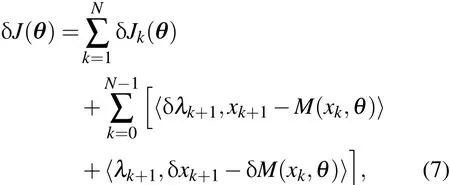
上式中δxk和δλk分别表示非线性映射状态向量和拉格朗日乘子向量的一阶变分.由(1)式显然有〈δλk+1,xk+1-M(xk,θ)〉=0.而目标泛函 J(θ)和向量函数M(xk,θ)的一阶变分按定义可以进一步写为
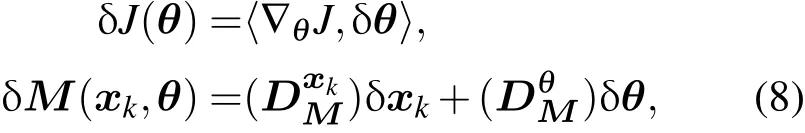
其中DMx k∈Rn×n和DθM∈Rm×n分别表示模式向量函数M(xk,θ)关于xk和θ的Jacobian矩阵.将(8)式中第二式代入(7)式右边第三项,同时利用恒等式和伴随性质〈λ,A x〉=〈ATλ,x〉可得

将(8)式中第一式与(6)式和(9)式代入(7)式并合并同类项.考虑到一阶变分δxk,δλk和δθ可以取任意值,且δx0=0,δxN/=0,进而可导出下面的方程组:
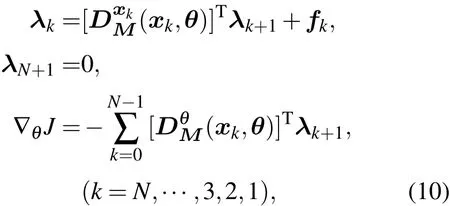
(10)式中的第一式称为伴随方程,λk表示k时次的伴随状态向量;从表达式易知,伴随方程积分之前必须求得非线性映射的状态向量序列xk,而且需按照顺序 k=N,N-1,···,1 进行逆向积分.(10)式中第二式给出了伴随方程的初值条件λN+1=0,因为是逆向积分,所以初值条件在末端时刻k=N+1给出.(10)式中的第三式是目标泛函关于未知参数向量梯度的表达式,计算梯度之前需要确定状态向量xk和伴随向量λk.在本小节中利用一阶变分方法获得了伴随方程和目标泛函梯度的公式,通过计算目标泛函梯度向量的值,进而利用基于一阶导数信息的最优化算法(共轭梯度方法和拟牛顿方法)可以估计未知参数[8,13].但是,在混沌系统参数估计中,完全依赖一阶导数信息的最优化算法通常收敛速度较慢,对于具有较高维数的强非线性混沌系统尤其如此.因此为了加快收敛速度,有必要研究能同时利用导数和精确Hessian矩阵信息的非线性映射未知参数估计方法.
3.2 二阶变分方法
为了导出Hessian矩阵-向量乘积及相关的二阶伴随方程的通用表达式,首先对(1)式求一阶和二阶变分,则分别得到相应的切线性系统(TLS):

和二阶切线性系统:

(11)式和(12)式中的δxk和δθ表示一阶变分或切线性向量,而δ2xk和δ2θ表示二阶变分或二阶切线性向量.
其次对(10)式中的伴随方程直接求一阶变分,并将伴随向量λk的一阶变分δλk用ζk表示(即ζk=δλk),则可得
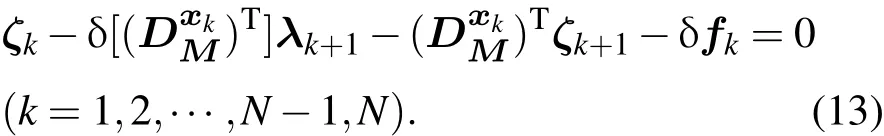
ζk称为二阶伴随向量,考虑到λN+1=0,进而可确定二阶伴随量的末端值为ζN+1=0.下面推导Jacobian矩阵Dhxk,DMxk和DθM的一维变分表达式.
因为

所以有

同理可得非线性模式函数向量Jacobian矩阵的一维变分表达式:

将(15)和(16)式代入(12)和(13)式,可得:

(17)式被称为非线性映射的二阶切线性模式,刻画的是二阶切线性向量从时刻k=0到k=N的演化;相应地,(18)式称为二阶伴随模式,刻画的是二阶伴随向量从时刻k=N到k=0的演化.对(17)和(18)式左右两端分别用-λk+1和δxk求内积,并将两式所得到的结果相加,则可得:
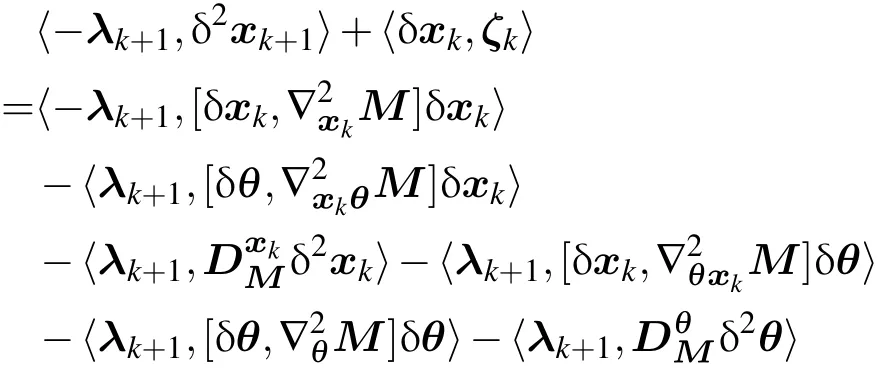

为了简化(19)式,利用伴随性质后有以下等式成立:
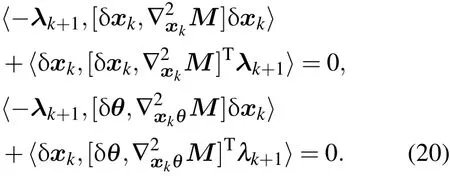
另一方面,由一阶切线性模式和一阶伴随模式可导出以下等式:
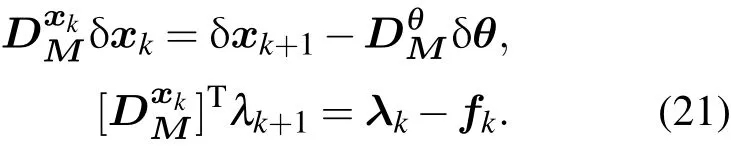
将(20)式和(21)式都代入(19)式,进行化简后可得:
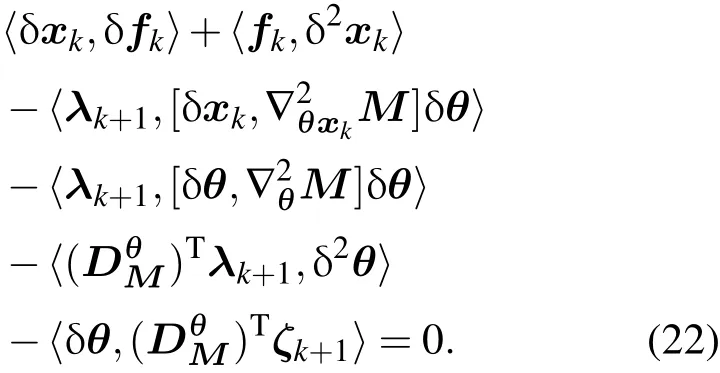
将链式法则应用到(4)式上,可以获得Jk(θ)的二阶变分表达式:

另外对 δJ(θ)= 〈∇θJ,δθ〉两边进行一阶变分运算,可以导出下式:
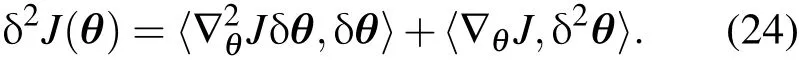
将(10)式中目标泛函梯度表达式代入(24)式,同时对(23)式左右两边从k=1到N求和,再考虑到进而得到:
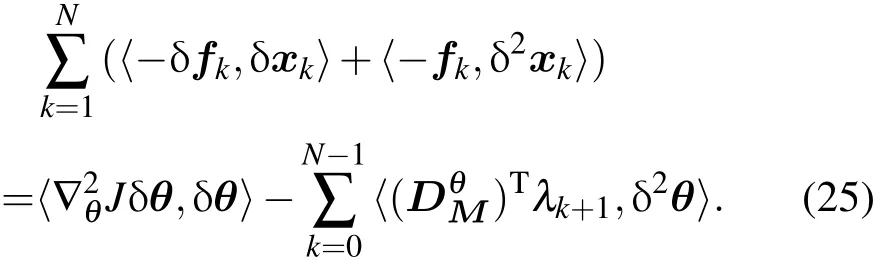
对(22)式左右两边从k=0到N-1求和,并与(25)式相加,化简后得到


考虑到一阶变分δθ的任意性,从而有
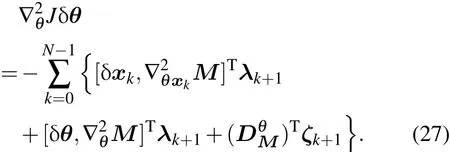
(27)式是目标泛函关于未知物理参数的Hessian矩阵-向量乘积的表达式,其显式给出了可以改善最优化算法性能的二阶导数信息,与Hessian矩阵相乘的向量δθ表示在每次最优化迭代过程中未知参数向量逼近物理参数真值时的增量.在本小节中利用二阶变分方法给出了切线性方程、二阶伴随方程以及计算目标泛函关于未知物理参数的Hessian矩阵-向量乘积的公式.从(27)式可知,在计算∇θ2Jδθ的值之前需要确定状态向量xk,一阶切线性向量δxk,伴随向量λk和二阶伴随向量ζk的值,因此需要依次求解非线性映射正模式(1),切线性模式(11),一阶伴随模式(10)和二阶伴随模式(18).其中,非线性映射系统和切线性模式需要进行正向积分,一/二阶伴随模式需要进行逆向积分.
3.3 算法流程设计
在导出目标泛函梯度∇θJ和Hessian矩阵-向量乘积∇θ2Jδθ的公式之后,可以选择合适的牛顿型最优化算法对未知物理参数向量进行迭代估计.本文中选用的是牛顿-共轭梯度方法(Newton-conjugate gradient method,NCG)[21,22].在NCG方法中使用共轭梯度方法近似求解牛顿方程∇2J(θk)sk=-∇J(θk),当牛顿方程的残余量足够小(即满足(28)式)或者遇到负曲率方向时,对共轭梯度方法能进行足够精确地截断.

在(28)式中ηk∈(0,1),确定方向矢量sk后,使用简单Armijo线搜索方法[21]能计算出步长大小αk.因为完整Hessian矩阵的直接计算和存储代价太高,所以不适合快速算法.而NCG方法的优点是只需要使用Hessian矩阵-向量乘积的值,因此本文3.2部分中利用二阶离散变分方法给出的(27)式正好能满足此要求.二阶离散变分方法估计非线性映射系统的未知参数的具体计算流程如图1所示,具体步骤说明如下.
第1步 设定未知物理参数向量的初始猜测值;
第2步 利用参数向量的新估计值,对非线性映射模式(1)进行正向积分,获得系统状态量的演化轨迹xk并加以存贮;

图1 二阶变分方法估计非线性映射参数的流程图
第3步 利用xk和yok根据(2)式计算目标泛函 J(θ)的值;
第4步 利用xk和yok和伴随初值条件,对伴随模式从k=N到k=1进行逆向积分,求得伴随向量的演化轨迹λk并加以存贮;
第5步 利用xk和λk根据(10)式中第三式求目标泛函关于各个未知物理参数的梯度向量值;
第6步 如果满足程序终止条件(如达到所要求的收敛精度或预先指定的最大迭代次数),则终止程序,同时获得非线性系统的参数估计值;若不满足,则继续进行下面的步骤;
第7步 利用演化轨迹xk和切线性量初值条件,对切线性模式(11)进行正向积分,获得切线性量或扰动量的演化轨迹δxk并加以存贮;
第8步 利用xk,δxk,λk和二阶伴随初值条件ζN=0,对二阶伴随模式(18)从k=N到k=1进行反向积分,求得二阶伴随向量的演化轨迹ζk并加以存贮;
第9步 利用xk,δxk,λk和ζk按照(27)式计算Hessian矩阵与未知参数向量增量之间的乘积;
第10步 将目标泛函梯度值和Hessian矩阵-向量乘积值输入到基于NCG方法的最优化程序中,计算出方向矢量和最优步长,进而利用θk+1=θk+αksk对未知物理参数向量进行迭代更新.利用新估计值从第二步开始进行新一轮的迭代循环.
4 数值仿真结果及分析
4.1 Hyperheno´n映射系统的参数估计
首先以典型的Hyperheno´n映射为例,研究二阶离散变分方法估计非线性映射系统中未知物理参数的有效性.Hyperheno´n映射的控制方程可表示如下:

当a=1.76和b=0.1时,该系统处于超混沌状态[19].状态向量表示为x=(x,y,z)T,θ=(a,b)T表示未知物理参数向量.目标是在获得x的观测量yko=(xok,yok,zok)T的情况下,辨识未知参数向量θ.通过比较(29)式与(1)式,易知非线性模式函数向量可表示为它的一阶变分为

(30)式中 δxk=(δxk,δyk,δzk)T和 δθ =(δa,δb)T分别表示xk和θ的一阶变分.根据(11)式可得切线性方程组:
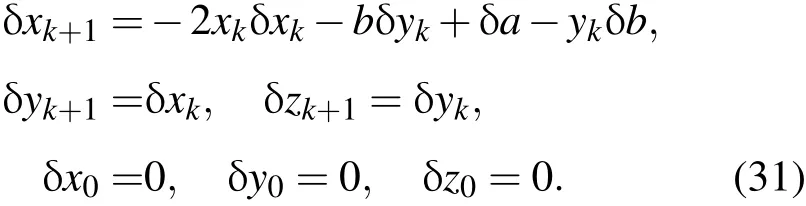
首先引入与xk对应的伴随向量序列λk=(λk,pk,qk)T,并将 xk,yko,λk,θ,(DMxk)T和 (DθM)T等的表达式代入(10)式中的第一和第三式,同时考虑到伴随初始条件,进而得到Hyperheno´n超混沌映射系统的伴随方程和目标泛函关于未知参数的梯度公式,分别如(32)和(33)式所示:
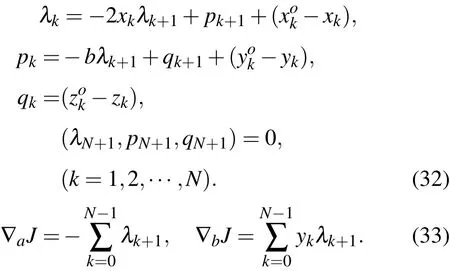
其次将λk,

和Dxk代入(18)式中,则得到Hyperheno´n映射系M统的二阶伴随方程:

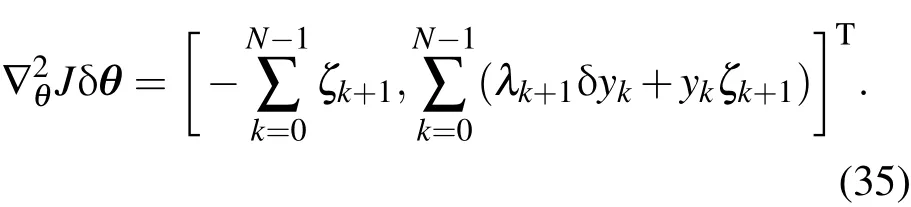
在仿真试验中,观测数据的采集过程如下:首先设定物理参数的真实值,让Hyperheno´n映射自由演化,在经历暂态过程之后任取混沌状态的一点作为初值,并以此时刻作为初始时刻;其次任其迭代演化至第N步,可获得Hyperheno´n映射的离散混沌状态序列xk(k=0,1,2,···,N).在本试验中,初始条件设定为混沌状态中一点:x0=0.8350073,y0=-0.8732880和z0=1.6236088,抽取前面4个状态量作为观测数据yko,(k=1,2,···,N);然后可在所选状态量上叠加高斯随机数作为观测噪声,噪声的均值取为0,标准偏差取为σo.因为在这种情况下观测误差协方差矩阵Rk为3×3大小的单位矩阵,所以离散形式的目标泛函表示如下:
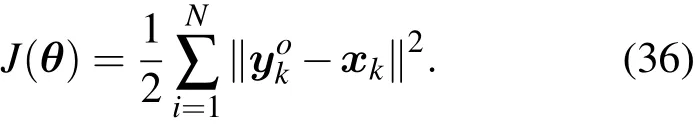
根据伴随方程、目标泛函及其梯度表达式,利用共轭梯度算法能对非线性映射的未知物理参数进行最优估计,这里称之为一阶变分方法;而根据一/二阶伴随方程、切线性方程、目标泛函、梯度及Hessian矩阵-向量乘积的表达式,利用NCG算法也能对非线性映射的未知物理参数进行最优估计,称之为二阶变分方法.在两个方法中,未知参数的迭代初值都设定为:θ0=(0,0,0)T.
图2和图3中分别给出了在采用一阶和二阶变分方法时目标泛函对数值和梯度模对数值随迭代次数的下?降图.?理论上当目标泛函关于未知参数的梯度模时,未知参数向量取最优估计值.但本文中为了减小计算代价,采用通常的迭代收敛标准,即前后两次?迭代的?目?标泛函梯?度模变化小于预先指定的阈值此时的计算误差小于机器误差,可以忽略.从图2和图3中可以看出,就目标泛函及其梯度值的变化而言,二阶变分方法的下降速度明显快于一阶变分方法.由表1进一步可知,前者达到收敛只需要经历8次迭代,而后者需要72次迭代;而且二阶变分方法达到收敛后的目标泛函值和梯度值比一阶变分方法都要小数个量级.图4和图5表示的是物理参数a和b的估计值在最小化过程中随迭代次数的变化以及逼近真实值的程度,从图中易知,采用二阶变分方法时估计值收敛到真值的速度明显高于一阶变分方法.分析和总结图2—5中所示的试验结果,可得如下结论:由于二阶离散变分方法能够同时利用目标泛函梯度信息和准确的Hessian矩阵信息,因此目标泛函能够快速下降,进而达到收敛.表1中给出了在无观测噪声情况下一/二阶离散变分方法对Hyperhen´on映射系统中未知物理参数进行估计的比较结果,容易得出结论:二阶离散变分方法用非常少的迭代次数获得了更高的估计精度.随着观测误差增加,虽然未知参数的估计精度下降,但在相同误差水平情况下二阶变分方法无论是在目标泛函迭代收敛速度还是在参数估计精度上都优于一阶变分方法,因篇幅限制具体情况不再赘述.
4.2 二维抛物映射系统的参数估计
在本部分中以二维抛物映射系统为例,进一步说明利用二阶离散变分方法估计非线性映射中未知参数的有效性.二维抛物映射可用离散方程表示如下:


图2 Hyperhen´on映射目标泛函值变化图
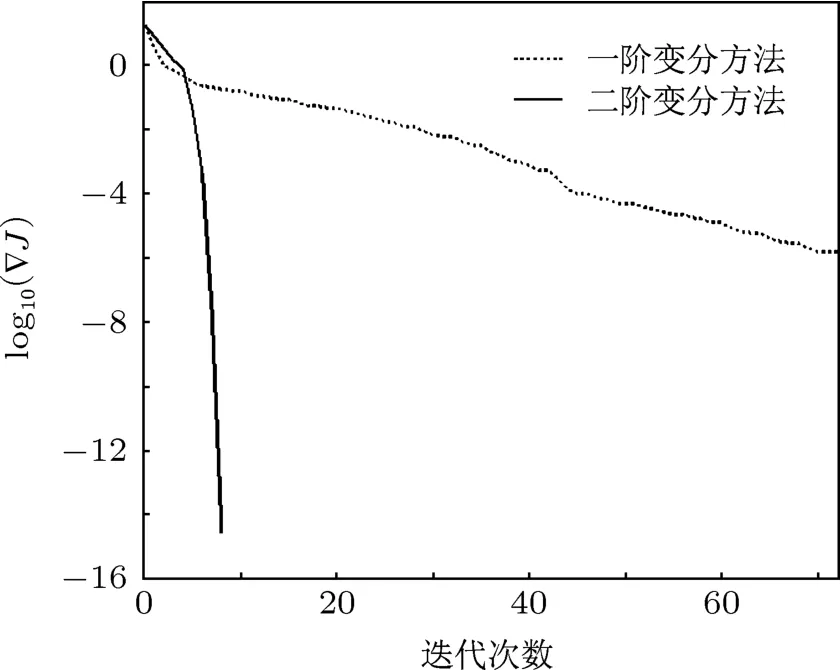
图3 Hyperhen´on映射泛函梯度值变化图

图4 Hyperhen´on映射参数a辨识曲线图
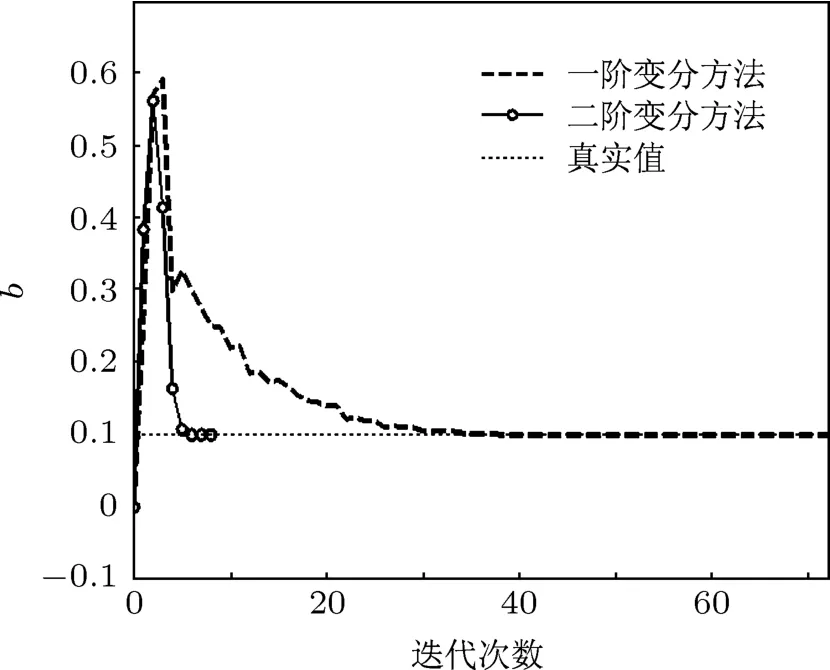
图5 Hyperhen´on映射参数b辨识曲线图

表1 无观测噪声时Hyperhen´on映射的参数估计结果
(37)式表示的是一个二维双参数离散迭代映射,两个控制参数a和b必须为正实数.a具有全局动态幅度调节功能,称之为幅度调节参数;而b具有动力学特性调节功能,称之为特性调节参数[20].当a=1.00和b=1.72时,二维抛物映射系统呈现混沌状态.设定状态向量x=(x,y)T和未知物理参数向量θ=(a,b)T,目标是在获得x的观测序列yko=(xok,yok)T的情况下,估计未知参数向量θ.
首先通过比较(37)式与 (1)式,易知M(xk,θ)=[ay2k,byk(1-xk)]T,其一阶变分为

根据(11)式可得切线性方程组:
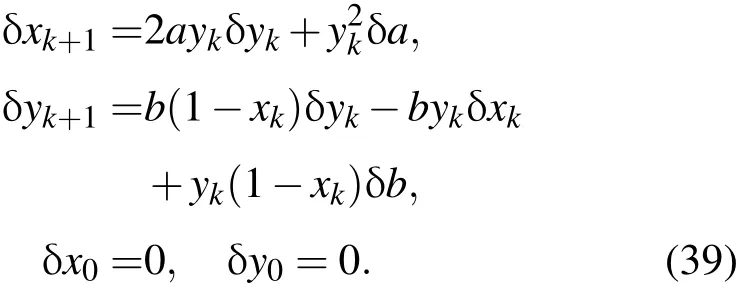
其次引入与xk对应的伴随向量序列λk=(λk,pk)T,并将 xk,yko,λk,θ,(DMxk)T和 (DθM)T等的表达式代入(10)式中的第一和第三式,同时考虑到伴随初始条件,进而得到二维抛物映射系统的伴随方程和目标泛函梯度公式,分别如(40)和(41)式所示:

中,则得到二维抛物映射的二阶伴随方程:
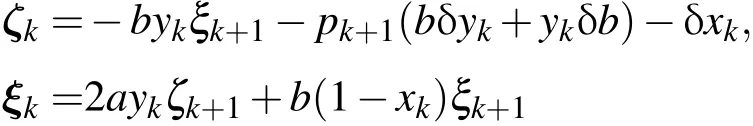
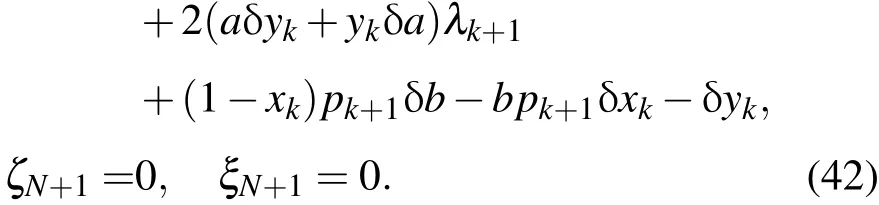

在仿真试验中,观测数据的生成采用与4.1部分中相同的方法.模式初始状态量(x0,y0)取为(0.0147653,-0.1697946),其是二维抛物映射混沌系统状态中一点.考虑到观测误差协方差矩阵是2×2大小的单位矩阵,目标泛函表示如下:

根据伴随方程、目标泛函及其梯度表达式,利用共轭梯度算法能对二维抛物映射的未知物理参数进行最优估计,称为一阶变分方法;而根据一/二阶伴随方程、切线性方程、目标泛函、梯度及Hessian矩阵-向量乘积的表达式,利用NCG算法能够对二维抛物映射的未知物理参数进行最优估计,称为二阶变分方法.两种方法中未知参数向量的迭代初值都设定为θ0=(0,0)T.最小化迭代收敛采用与4.1部分中相同的准则.
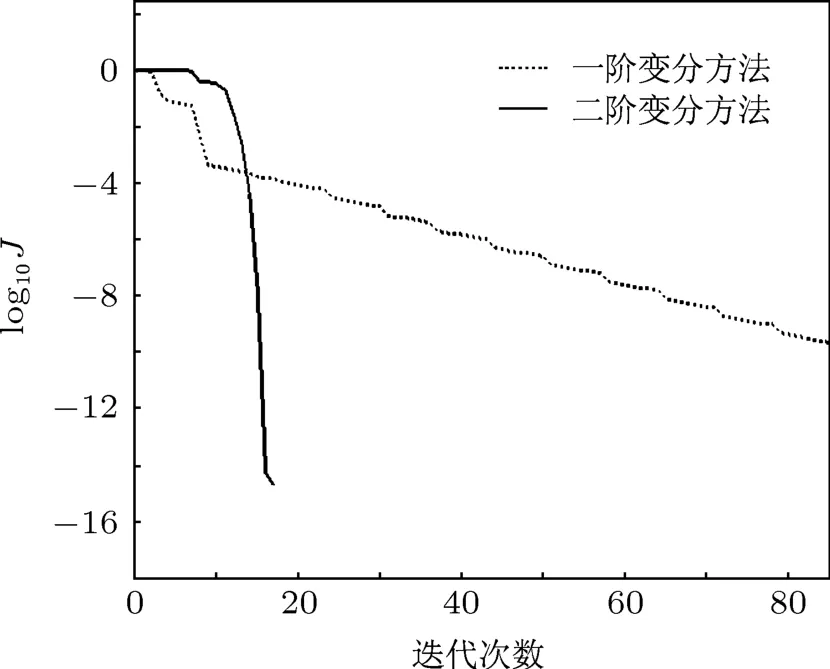
图6 二维抛物映射目标泛函值变化图

图7 二维抛物映射泛函梯度值变化图
在二维抛物映射系统的未知物理参数估计中,图6和7中分别给出了在采用一阶和二阶变分方法时目标泛函对数值和梯度模对数值随迭代次数的下降图.从图6和7中易知:就目标泛函及其梯度模对数值的变化而言,二阶变分方法的下降速度明显快于一阶变分方法.由表2进一步可得:前者达到收敛只经历17次迭代,而后者需要85次迭代.同时,二阶变分方法达到收敛后的目标泛函值和梯度模值比一阶变分方法都要小数个量级.图8和图9展示的是二维抛物映射系统中参数a和b的估计值随迭代次数的变化及其逼近真实值的程度,从图中易知:在利用二阶变分方法估计两个未知物理参数时,收敛速度都快于一阶变分方法,而对参数a估计的收敛速度差异更明显.表2中分别给出了在无观测噪声情况下一/二阶离散变分方法对二维抛物映射系统中未知参数进行估计的比较结果:一阶变分方法对参数a和b的估计精度分别是小数点后3位和4位,而二阶变分方法对两个参数的估计精度都能达到小数点后7位.根据上面的分析归纳出如下结论:因为二阶离散变分方法能够同时利用准确的目标泛函梯度和Hessian矩阵信息,所以能够用更少的迭代次数获得更高的估计精度,明显优于一阶变分方法.上述结论在不同观测误差水平情况下仍然成立,由于篇幅所限不再赘述.
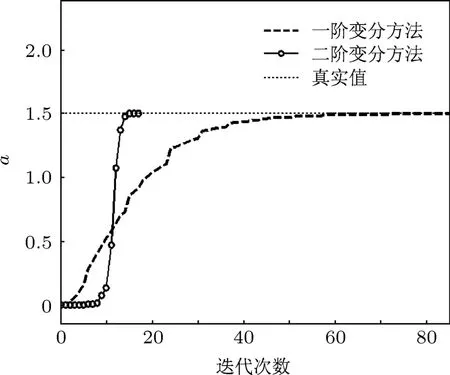
图8 二维抛物映射参数a的辨识曲线图

图9 二维抛物映射参数b的辨识曲线图

表2 无观测噪声时二维抛物映射的参数估计结果
5 结论
本文提出一种估计非线性映射未知物理参数向量的二阶离散变分方法.首先针对xk+1=M(xk,θ)形式的非线性离散混沌系统,通过拉格朗日乘子将系统的状态控制方程引入到目标泛函中,将映射方程约束最优化问题转换为无约束最优化问题;其次利用变分方法给出了一/二阶伴随方程、目标泛函梯度和Hessian矩阵-向量乘的显式表达式;然后设计了估计非线性映射未知参数的新算法,并以此对Hyperhen´on映射和二维抛物映射中的未知参数进行了估计.数值仿真结果表明了二阶离散变分方法的有效性和优点:因为能够同时利用准确的目标泛函梯度信息和与Hessian矩阵相关的二阶信息,所以二阶变分方法在无论有无观测噪声的情况下都能够用较少的迭代次数获得更高的估计精度,明显优于一阶变分方法.该方法可推广应用于其他类型非线性映射和混沌系统的未知物理参数估计中.
[1]Liu FC,Liang X M 2005 Acta Phys.Sin.54 4584(in Chinese)[刘福才,梁晓明2005物理学报54 4584]
[2]Wang X Y,Wu X J2006 Acta Phys.Sin.55 605(in Chinese)[王兴元,武相军2006物理学报55 605]
[3]Wu Z Q,Tan F X,Wang SX 2006 Acta Phys.Sin.55 1651(in Chinese)[吴忠强,谭拂晓,王绍仙2006物理学报55 1651]
[4]Maybhate A,Amritkar RE 1999 Phys.Rev.E 59 284
[5]Parlitz U 1996 Phys.Rev.Lett.76 1232
[6]He M F,Mu Y M,Zhao L Z 2000 Acta Phys.Sin.49 830(in Chinese)[贺明峰,穆云明,赵立中2000物理学报49 830]
[7]Guan X P,Peng H P,Li L X,Wang Y Q 2001 Acta Phys.Sin.50 26(in Chinese)[关新平,彭海朋,李丽香,王益群2001物理学报50 26]
[8]Cao X Q,Song JQ,Zhang W M,Zhao J,Zhang L L 2011 Acta Phys.Sin.60 070511(in Chinese)[曹小群,宋君强,张卫民,赵军,张理论2011物理学报60 070511]
[9]Gao F,Tong H Q 2006 Acta Phys.Sin.55 577(in Chinese)[高飞,童恒庆2006物理学报55 577]
[10]Li L X,Peng H P,Yang Y X,Wang X D 2007 Acta Phys.Sin.56 51(in Chinese)[李丽香,彭海朋,杨义先,王向东2007物理学报56 51]
[11]Wang JY,Huang D X 2008 Acta Phys.Sin.57 2755(in Chinese)[王钧炎,黄德先2008物理学报57 2755]
[12]Long W,Jiao JJ 2012 Acta Phys.Sin.61 110507(in Chinese)[龙文,焦建军2012物理学报61 110507]
[13]Cao X Q,Zhang W M,Song JQ,Zhu X Q,Zhao J 2012 Acta Phys.Sin.61 020507(in Chinese)[曹小群,张卫民,宋君强,朱小谦,赵军2012物理学报61 020507]
[14]Huang SX,Wu R S 2001 Mathematical Physics Problems in Atmosphere Science(Beijing:Meteorology Press)(in Chinese)[黄思训,伍荣生2001大气科学中的数学物理问题(北京:气象出版社)]
[15]He JH 2008 Int.J.Modern.Phys.B.22 3487
[16]He JH 2000 Appl.Math.Mech.21 797
[17]He JH 2001 Int.J.Nonlin.Sci.Numer.2 309
[18]He JH,Lee EWM 2009 Phys.Lett.A 373 1644
[19]Chen ED 2005 Ph.D.Dissertation(Dalian:Dalian University of Science and Technology)(in Chinese)[陈尔东2005博士学位论文(大连:大连理工大学)]
[20]Meng JD,Bao B C,Xu Q 2011 Acta Phys.Sin.60 010504(in Chinese)[孟继德,包伯成,徐强2011物理学报60 010504]
[21]Kelley C T 1999 Iterative Methods for Optimization(Philadelphia:SIAM)p95
[22]Nocedal J,Wright SJ2006 Numerical Optimization(2nd Ed.)(Verlag,Berlin,Heidelberg,New York:Springer)p198
