RBCC动力飞行器等动压爬升方法①
2013-09-26闫晓东贾晓娟
闫晓东,贾晓娟,吕 石
(1.西北工业大学航天学院,西安 710072;2.航天飞行动力学技术重点实验室,西安 710072)
0 引言
火箭基组合循环推进系统(Rocket Based Combined Cycle,RBCC)将高推重比、低比冲的火箭发动机和低推重比、高比冲的吸气式发动机有机地组合在一起,可实现航天推进的高效性与经济性的最佳组合[1],有望为未来空天飞行器提供先进的推进系统。国内外学者已经对RBCC动力空天飞行器进行了大量的论证和设计工作[2-4]。
与传统火箭动力相比,由于吸气原因,RBCC发动机的性能与飞行环境密切相关。为保证其稳定工作在一个最优或稳定状态,一般RBCC动力飞行器上升段采用等动压爬升方法,即当飞行器达到一定动压后,保持动压不变进行加速和爬升。文献[5]提出了一种基于B样条建立马赫数-动压参考曲线,然后通过二分法迭代攻角,以跟踪参考曲线的RBCC飞行器爬升轨迹设计方法,未给出等动压爬升的轨迹设计方法。文献[6]提出了一种等动压爬升的迭代方法,但未给出迎角的计算方法。文献[7]尝试采用优化的方法,以获得RBCC动力重复使用运载器最优的爬升轨迹,其优化结果是非等动压的。文献[8]提出了3种迎角的优化设计模型,以在POST中实现等动压爬升,但这些模型设计参数多,只能通过优化的方法予以确定,因而不能提供实时的等动压爬升攻角制导指令。
本文通过推导等动压爬升的高度-速度代数方程,提出了一种基于高度-速度曲线的等动压爬升方法,可为吸气式飞行器的等动压乃至非等动压爬升提供一种快速参考轨迹生成和制导方法。
1 动力学方程
不考虑地球旋转,纵向平面内的质点动力学方程可写为
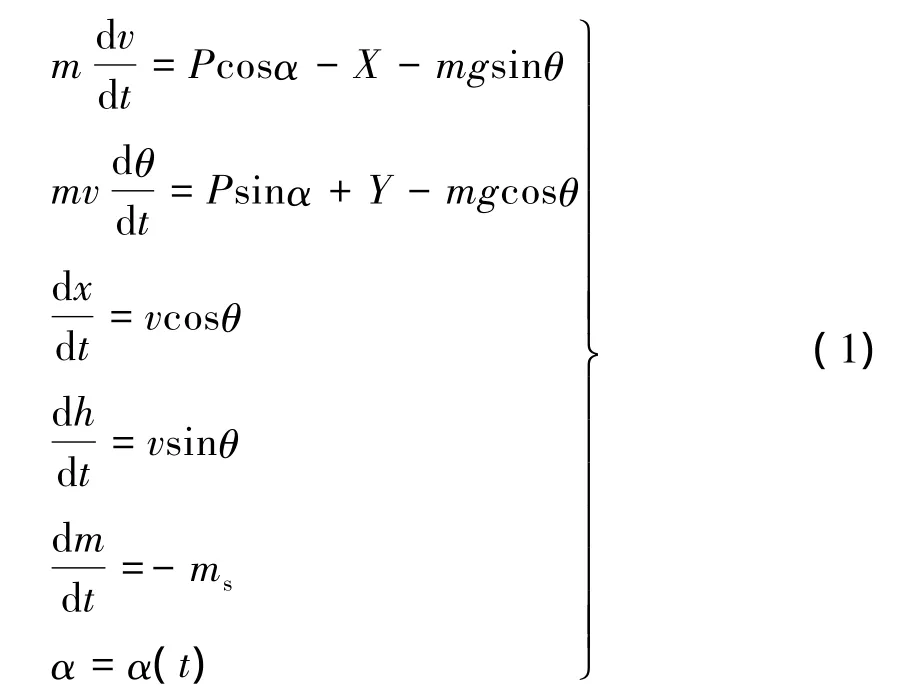
式中 m为飞行器质量;g为重力加速度;v为速度;θ为弹道倾角;x、h分别为水平距离和高度;ms为发动机秒耗量;α为迎角,α(t)表示迎角的变化规律;X、Y分别为气动阻力和升力;P为发动机推力。
P可由式(2)计算:

式中 Isp(α,Ma,H)为发动机比冲,是迎角、马赫数及高度的函数。
2 等动压爬升轨迹
在RBCC动力空天飞行器的爬升过程中,动压可表示为

式中 q为动压;ρ为大气密度。
考虑指数形式的大气密度:

式中 ρ0为基准大气密度;hs为参考高度,常数。
对动压求导,可得
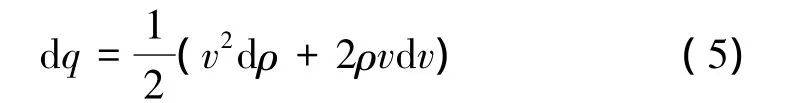
将式(4)代入式(5)中,有

考虑到等动压爬升dq=0,且将式(6)代入式(5)中,有

对式(7)求积分,可得

式中 Cv为常数,由等动压爬升的动压常数唯一确定。
由式(8)不难发现,只要飞行器在爬升过程中满足该高度和速度代数方程,就可实现等动压爬升。本文将该高度-速度的关系式称为等动压线。要说明的是当Cv不再为常数时,如Cv=f(v),则动压就不再是常数,而是速度v的函数,此时的动压变化规律就可由该函数确定,据此可灵活设计出各种满足爬升需求的高度-速度参考曲线或动压-速度参考曲线。
3 等动压爬升轨迹实现方法
由式(8)可知,只要沿着等动压线飞行,就可实现等动压爬升。若假设推力P(α,Ma,H)已知,则等动压爬升是一个典型的单输入、单输出的非线性跟踪控制问题。基于反馈线性化方法[9-10],可推导出等动压爬升的迎角制导指令。
方程组(1)的状态变量为 X=[v,θ,X,H,M]T。为了跟踪等动压线,选取系统输入u=α,输出y=h,依据反馈线性化方法,现对方程组(1)的第4式求导:

基于等动压线,参考高度的导数可表示为

将式(8)代入式(10)中

对式(11)求二阶导:
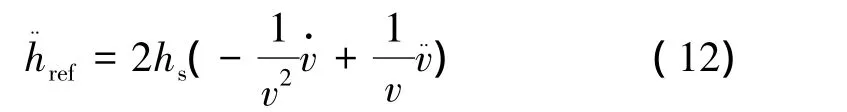
将式(12)代入到方程(9)中,可得跟踪等动压线的弹道倾角:

考虑到吸气式爬升过程中迎角较小,可令sinα≈α,并将升力Y表示为Y=Yαα,Yα为升力对迎角的偏导数,且有

将式(13)代入方程组(1)的第2式,可得等动压爬升的参考迎角指令为

为减小等动压线跟踪的稳态误差,且补偿参数干扰或建模不确定性的影响,考虑如下迎角补偿:
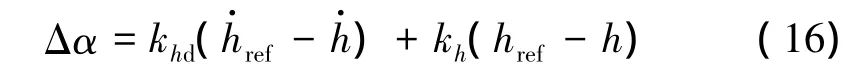
其中,khd和kh为调节系数,可取为

式中 ζ为阻尼系数,可取为0.7;ωn为自然频率,可根据飞行器实际控制能力确定。
最终,等动压爬升的迎角制导指令为
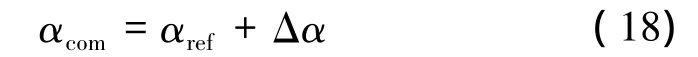
4 仿真算例
以某RBCC飞行器为例,对本文所设计的等动压爬升方法进行仿真验证。该飞行器的参考面积为9.3 m2,飞行器初始质量为52 000 kg,等动压爬升阶段推进剂秒耗量为60 kg/s,等动压爬升的初始条件如表1所示。升力系数和阻力系数分别为

发动机比冲拟合公式为
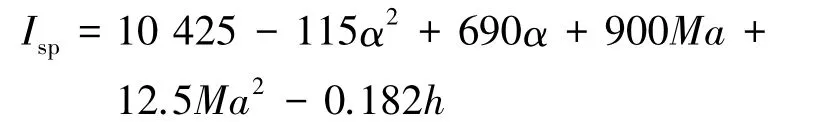
需要指出的是,该比冲拟合公式仅在一定范围内可用,不能应用于RBCC发动机全程的性能计算。

表1 弹道初始条件Table 1 Initial conditions of trajectory
4.1 仿真结果
飞行器按照42 kPa等动压爬升,将初始高度和速度代入到式(7)中,不难得到Cv=-72 063。
除能够实现等动压爬升外,还可实现按某一规律进行爬升。本算例给出了一种动压随速度增加的爬升方法。令

其中,令C1=-71 063,则爬升过程中动压由42 kPa变化到52 kPa。
4.2 结果分析
该飞行器从Ma=3.4开始爬升,并到Ma=8结束(图1),经历了亚燃冲压模态和超燃冲压模态。图2表明,等动压爬升过程中可实现预定等动压线的良好跟踪,且动压一直保持在42 kPa左右,变化幅度很小(如图3所示)。可见,本文提出的方法可精确地实现等动压爬升。图4表明,在爬升过程中,制导指令αcom通过跟踪高度-速度等动压线实时生成,迎角指令平滑,保持在5°以内。

除了可实现等动压爬升外,该方法也可实现非等动压爬升轨迹设计。图6表明,该方法可按照预定的非等动压规律进行爬升。由图5不难发现,非等动压爬升与等动压爬升相比,由于动压逐渐增加,因而在相同的终端速度下,高度较低,较低的高度也导致迎角较小(图4)。

5 结论
(1)RBCC动力飞行器吸气式爬升过程速度变化范围大,推力性能与飞行状态密切相关,因而设计合适的爬升轨迹对于RBCC动力飞行器性能充分发挥具有重要作用。
(2)本文设计的等动压爬升方法可完成RBCC动力飞行器的等动压爬升。此外,该方法可综合考虑热流、动压等约束,完成RBCC动力飞行器的各种爬升规律的轨迹设计,具有设计过程简单、便于跟踪的优点,并可扩展到其他吸气式飞行器的轨迹设计中。
[1]刘洋,何国强,刘佩进,等.RBCC组合循环推进系统研究现状和进展[J].固体火箭技术,2009,32(3):288-293.
[2]David A Young,Timothy Kokan.Lazarus:a SSTO hypersonic vehicle concept utilizing RBCC and HEDM propulsion technologies[R].AIAA 2006-8099.
[3]Kevin W Flaherty,Katherine M Andrews,Glenn W Liston.Operability benefits of airbreathing hypersonic propulsion for flexible access to space[J].Journal of Spacecraft and Rockets,2010,47(2):3-4.
[4]Ajay P Kothari,John W Livingston,Christopher Tarpley,et al.A reusable,rocket and air-breathing combined cycle hypersonic vehicle design for access-to-space[R].AIAA 2010-8905.
[5]吕翔,何国强,刘佩进.RBCC飞行器爬升段轨迹设计方法[J].航空学报,2010,31(7):1331-1337.
[6]薛瑞,胡春波,吕翔,等.两级入轨RBCC等动压助推弹道设计与推进剂流量分析[J].固体火箭技术,2013,36(2):155-160.
[7]龚春林,韩璐.RBCC可重复使用运载器上升段轨迹优化设计[J].固体火箭技术,2012,35(3):290-295.
[8]Olds J R,Budianto I A.Constant dynamic pressure trajectory simulation with POST[R].AIAA 98-302.
[9]闫晓东,唐硕.基于反馈线性化的亚轨道飞行器返回轨道跟踪方法[J].宇航学报,2008,29(5):1546-155.
[10]姚郁,译.非线性系统设计[M].北京:电子工业出版社,2006.
