考虑低燃温燃气发生器试验的弹射器内弹道性能预示①

2013-09-26惠卫华鲍福廷

固体火箭技术 2013年6期

惠卫华，鲍福廷，刘旸

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

纯燃气弹射分离方式因其结构设计、数学模型简单，已经成为弹道导弹、潜射导弹及地空导弹弹射过程中一种有效的弹射选择模式。低燃温高燃速药型［1］的出现，也使纯燃气弹射分离装置的广泛使用成为可能。

目前，纯燃气弹射模式下的低压室内弹道计算主要采用理论分析方式进行［2－7］。笔者在前期也进行了纯燃气水面弹射内弹道求解的相关研究，并编写程序实现了相关软件［8］。在实际工程应用中，往往是先要进行单纯燃气发生器试验，获取高压室参数曲线，并校正一些效率参数，而后进行全系统内弹道分析。工程中，考虑试验的计算方法本质是一种校正后的理论算法，与直接调用试验数据曲线进行计算有一定区别，且使用较麻烦。所以，急需一种能够直接调用试验数据进行低压室内弹道及运动学计算的仿真系统来解决这一问题。但该模型在各种文献中少有提及，尤其是把这种计算过程编写程序形成软件的，更是在文献中没有出现。

引入试验曲线的计算方式与理论计算的差别，主要在于计算过程和计算参数的不同。因为理论计算中燃气的累积流量是从燃面推导理论计算出的，而引入试验的情况下，该值是通过压强和推力曲线反推出来的，且该值恰好是影响低压室压强和温度的重要参数，最终造成弹射分离运动学过程的差别。

本文建立考虑试验的弹器分离纯燃气弹射内弹道方程组，对该弹射过程中影响因素进行分析;同时，基于VC++.net软件，编写完整的内弹道求解程序，建立与工程实际结合紧密的“半经验”内弹道求解程序。

1 导弹未动前低压室内弹道求解数学模型

1.1 考虑试验数据的低压室内弹道方程组

燃气发射器试验数据可直接提供高压室内的压强-时间曲线参数，于是可省去计算高压室内弹道的过程。引入压强-时间曲线参数后，可求出特征速度及流出气体总流量;依据能量方程和状态方程，按时间步求出发射筒内压强和温度;然后，根据温度和压强参数，可获取相关运动学参数。

具体求解过程如下:

式中 C*代表特征速度;Gc［i］代表第i步燃气秒流量;Wb［i+1］代表第i+1步燃气流出总流量。

1.2 纯理论计算高低压室联立内弹道方程组

燃气发生器高压室内弹道按照四阶龙格库塔方法进行，以燃烧室内气体密度和压强为关注参数，依步长求解。在获取每个时间步高压室压强、温度基础上，求解燃气秒流量。然后，依据能量方程和状态方程，求解低压室温度和压强:

式中 pb为燃烧室压强;ρb为燃烧室混合气体密度;V为燃烧室自由容积;Mb为主装药燃气生成率;Mig为点火药燃气生成率;Gc为经喷管流出的燃气秒流量;cv为燃烧室内混合气体的比定容热容;cpb为装药燃气的比定压热容;Tpb为装药燃气的定压燃烧温度;cpig为燃烧室内混合气体的比定压热容;Tpig为点火药燃气的定压燃烧温度;cp喷管出口燃气的比定压热容。

1.3 2种计算方式的比较

从计算方程组可看出，考虑试验数据的计算与理论计算低压室内弹道计算过程有一定差别。

(1)计算流程不同

理论计算内弹道中，燃气秒流量是在高压室压强温度求解的基础上，按时间步求解特征速度后进行求解的;考虑试验数据输入计算内弹道，是采用试验得到的参数曲线，反推得到特征速度，然后进行求解的。

(2)计算中的参数不同

理论计算内弹道中，因为每个时间步会求解一个温度值，因而求解得到的特征速度在每个时间步是不同的，造成燃气秒流量的差别;考虑试验数据输入计算的内弹道，特征速度是一个恒定值，这是两者计算的主要差别。

2 不同弹射方式下的运动学方程组

2.1 地面弹射低压室内弹道方程组

地面弹射中，发射筒始终固定在发射架或发射车上，低压室内气体压强做功全部用于导弹加速。

式中 M1为导弹和运载器的质量;v1为导弹的速度;L1为导弹的绝对行程;pt、pa分别为低压室内压强和当前大气压强;F1为弹所受阻力;Tt为低压室温度。

2.2 水面弹射低压室内弹道方程组

根据质量守恒、能量守恒及状态方程，同时考虑弹器运动阻力和水的浮力，联合建立内弹道方程组，如式(3)。根据四阶龙格库塔微分方程求解方法，按时间步长求解相关参数，即可求得关心的低压室相关参数、导弹及运载器相关运动学参数。

式中 M1、M2分别为导弹和运载器的质量;v1、v2分别为导弹和运载器的速度;L1、L2分别为导弹和运载器的绝对行程;Le、L0、Ldown分别为导弹有效行程、点火前运载器出水距离和运载器在水下深度;pt、pa分别为低压室内压强和当前大气压强;Tt为低压室温度;v0为弹器弹射点火瞬间的初速。

为验证结果方便，按照导弹向上运动方向为正，运载器向下方向为正。

3 弹射系统内弹道分析软件系统

依据以上方程组，基于VC.net编程软件，编写了弹射系统内弹道分析软件。系统具备对地面、水面和空气中弹射过程内弹道分析的能力，还可考虑燃气发生器试验数据分析低压室内弹道的能力，如图1所示。

在输入栏内，输入相关导弹、运载器、燃气、空气、点火药、环境、计算设定等方面的参数，调取试验压强-时间数据，完成初始状态输入。点击“计算”，即可完成整个高低压室的内弹道计算。可根据弹射情况的不同，输出有效耗药量、导弹行程、导弹速度、导弹加速度、高压室压强、低压室压强、低压室温度、运载器速度、运载器过载、运载器水下距离等曲线及参数，如图2所示。

4 计算实例及分析

计算初始参数如表1所示。

计算在地面、水面2种不同弹射环境下，导弹获得分离速度、加速度情况。同时，结合燃气发生器试验数据输入，计算获得另一组弹器分离时导弹的速度和加速度。对2组数据进行对比分析，产生对设计有针对性的参考校准结果。

表1 初始弹射参数及设计指标Table 1 Initial launch parameter and design target

4.1 燃气发生器高压室内弹道

在同样的装药设计前提下，进行高压室内弹道的理论计算，按照方程组(2)进行计算，可获得燃气发生器高压室内弹道曲线，如图3(a)所示，燃气发生器高压室试验曲线如图3(b)所示。

4.2 地面理论弹射结果

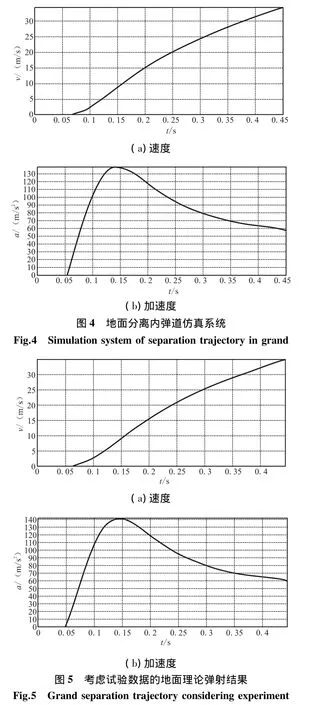
依据地面弹射内弹道方程组(3)求解，如图4所示。可获得以下导弹弹射分离速度结果:导弹分离速度达 34.321 m/s，最大加速度达 138.581 m/s2。

4.3 考虑试验数据的地面理论弹射结果

依据给定的燃气发生器高压室内弹道压强-时间参数，采用试验参数计算内弹道方程组(1)及地面弹射内弹道方程组(3)，可获得以下地面弹射分离时导弹速度结果，如图5所示。

从结果看出，导弹分离速度达34.809 m/s，与理论计算相对误差为 1.4%;最大加速度达 141.160 m/s2，与理论计算相对误差为1.86%。速度与加速度误差均在误差允许范围内。

4.4 水面理论弹射结果

依据水面弹射内弹道方程组(4)求解，可获得导弹弹射分离速度结果，如图6所示。导弹分离速度达23.610 m/s，最大加速度达 85.750 m/s2。从结果上看，水面弹射的速度和加速度都比地面弹射的参数小。这主要是由于弹器“双向”造成，能量用于对导弹和运载器的双重做功，引发能量分散消耗，促使导弹相关参数下降。