底部排气弹三维湍流燃烧的数值模拟①

卓长飞，武晓松，封 锋

(南京理工大学机械工程学院，南京 210094)

0 引言

导弹、炮弹等飞行器以超声速飞行时，气流在飞行器头部产生激波，从而产生激波阻力;接着，气流在飞行器底部发生大分离，形成低速、低压的回流区，在飞行器底部与头部形成较大的压力差，从而产生底部阻力。底部排气减阻的方法是在飞行器底部安装不带喷管的火箭发动机，该火箭发动机燃烧室压力非常低，燃气以亚声速排出，亚声速的高温燃气在底部与与初始回流区相互作用，能改变底部流场结构，达到提高底部压力、减小阻力、增大射程的目的［1］。底排减阻增程技术主要用于超声速飞行的炮弹中(底部排气增程弹)。

20世纪70年代前，底部排气弹研究人员对底部排气减阻效果研究大多采用向底部排冷、热空气的办法，研究底部排气对底部流场流动状态的影响，得到一些结论性的成果，为早期的底部排气弹设计所采用。70年代以后，研究人员直接采用底排装药进行风洞实验，发现有些用排放冷热空气得到的结论，与利用实际药剂试验得到的结论并不完全一致;有的虽然总体趋势较一致，但在数值上有较大差别;也有的结论完全不同［1］。常见的底排装药在贫氧条件下不能完全燃烧，排向底部区域的气体是由CO、H2等富燃气体组成。富燃气体在底部与来流新鲜空气接触混合可能会发生二次燃烧，继续对尾迹区排放热量，并改变底部流场结构。真实的底部装药排气对外流来说是一种异质流，同时在尾流场还可能存在二次燃烧和两相流效应，这是导致在数值或风洞实验中采用底排热空气和底排装药真实气体得到的结论有差别的原因。

国外关于数值研究底部排气弹底排真实气体底部燃烧的公开文献有:Charles J［2］采用层流流动模型和层流燃烧有限速率基元反应模型，模拟了M864弹的二维轴对称流场;Petri K［3］采用 k－ε湍流流动模型和层流燃烧有限速率基元反应模型，模拟了155 mm弹的三维流场;Jeong-Yeol［4］采用 k－ω 湍流流动模型与层流燃烧有限速率基元反应模型，模拟了155 mm弹的二维轴对称流场。这些国外文献虽然考虑了湍流流动模型，但仅采用层流有限速率基元反应模型模拟燃烧，没有考虑超声速底部流动中强湍流特性对燃烧的影响。国内数值研究底部排气弹主要以排冷、热空气为主，暂时没有发现对底部排气弹底排真实气体效应开展数值模拟的报道。因此，有必要开展底部排气弹底部真实气体效应数值研究，建立底部排气弹湍流流动与燃烧模型，充分考虑底部排气的异质流和二次燃烧效应，以便更加符合实际问题。

本文发展了一套多块结构网格三维湍流流动与燃烧的计算软件MSTCS-3D(Multi-block Structure Turbulent and Combustion Solver-3D)，考虑底部排气的真实气体效应，采用k－ω SST湍流流动模型、有限速率化学动力学基元反应模型和二阶矩湍流燃烧模型，建立了完整的底部排气弹底部湍流流动与燃烧模型，重点模拟了底部排气弹底排真实气体底部二次燃烧现象。研究了底排热空气/底排真实气体、来流马赫数对底部流场结构和底部压力分布的影响，以及底排真实气体发生二次燃烧的主要区域和燃烧过程，进一步深化了超声速底部排气燃烧减阻机理的认识，为后续研究奠定了坚实的基础。

1 数值方法

1.1 控制方程

在三维笛卡尔坐标系下，微分守恒形式的雷诺时均(RANS)化学非平衡流 Navier-Stokes方程［5］为

式中 U为守恒变量;F、G、H为无粘对流通量;Fv、Hv、Gv为粘性通量;S为化学反应源项。

这里仅列出守恒变量、无粘通量和化学反应源项的表达式:

式中 ρ为混合气体密度;u、v、w为3个方向速度;p为混合气体压力;Fi(i=1，…，N－1)为 i组分质量分数;N为总组分数;E为混合气体单位体积的总内能。

式中 h为混合气体单位质量焓。

各组分的质量反应生成率ωi由基元反应的动力学模型给出:

式中 Mi为第i中组分的摩尔质量;Rfj、Rbf分别代表摩尔浓度表示的第j个基元反应的正反应和逆反应的速率。

各符号详细意义见文献［5］。

1.2 湍流流动模型

Menter提出的 k－ω SST 两方程湍流模型［6］集合了k－ε和k－ω两种湍流模型的优点，是一种在工程上得到广泛应用的混合湍流模型，其湍动能输运方程和湍流比耗散率方程为

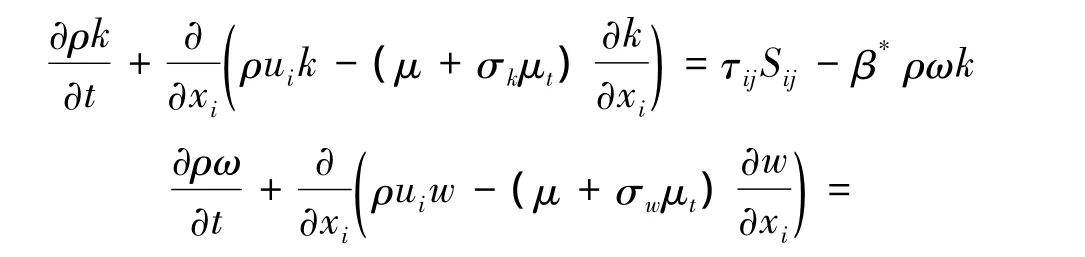
各符号详细意义和模型参数见文献［6］。

1.3 化学反应动力学模型与湍流燃烧模型

底部排气弹排出的富燃气体主要是由 CO、H2、CO2、H2O、N2组成等。因此，采用CO-H2-O2化学反应系统。本文采用 8 组分(CO、H2、O2、CO2、H2O、H、OH、O)12步基元反应的CO-H2-O2系统化学反应模型［2］，基元反应表达式和系数如表1所示。

考虑到超声速底部流场具有较强湍流特性，本文选择二阶矩湍流燃烧模型，控制湍流-化学反应相互作用机理［7］:

其中，带横线的单个符号表示时均值，带横线的2个符号表示两者脉动关联量。这里认为式中所有关联量，包括反应率系数k和浓度脉动的关联量都服从代数输运定律。只有反应速率系数k本身的时均值要PDF来确定，即

式中 p(T)是温度的概率密度函数(PDF)。

如果给定温度脉动的PDF为双δ分布，则

表1 CO-H2-O2基元反应模型Table 1 Detailed reaction model for CO-H2-O2

1.4 计算格式与计算方法

为了很好地捕捉激波、膨胀波等流场细节，空间离散采用三阶MUSCL重构方法和Steger-Warming矢通量分裂方法［8］，粘性项采用中心格式离散，时间离散采用单步推进，并采用局部时间步长法加速收敛。

在求解带化学反应的Navier-Stokes方程时，采用时间算子分裂的方法来处理刚性问题，即把求解流动偏微分方程时采用的时间步长进一步细分，作为求解化学反应刚性常微分方程的步长，计算化学反应对流场的贡献。具体做法是先冻结化学反应求解得到流场参数;然后，将化学反应看做等容放热或吸热过程，保持内能、速度参数不变，计算各组分的质量变化率;最后，迭代求解温度［9］。

1.5 计算模型与边界条件

本文采用155 mm SOC炮弹作为研究对象，计算网格如图1所示。由于尾迹区湍流流动特性较强，因此对尾迹区网格进行加密。本文暂不考虑飞行攻角和炮弹旋转，各流场参数的周向梯度为0，为节省计算量，取全弹的一半为计算区域，且周向分布13个网格。

底部排气弹的表面采用无滑移非催化壁面条件，计算区域的外边界采用远场边界。底部排气弹的排气口处采用亚声速入口边界，并且给定排气参数I和排气总温T0。排气参数是底排装置排气质量流率与炮弹迎面空气质量排开率之比，数学定义式为

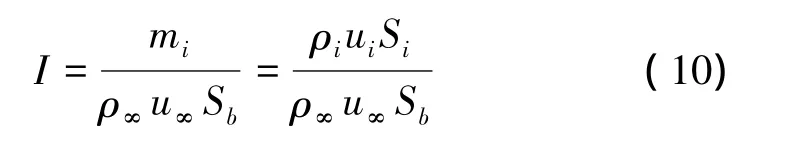
式中 下标“i”表示排气界面的物理参数;mi为排气质量流率;Si和Sb分别表示排气面积和弹底面积。

令Si/Sb为排气面积之比。本文所有算例计算均取Si/Sb=0.094 8。当底排热空气时，其组分和质量分数与来流空气一致(O2∶N2=0.23 ∶0.77);当底排真实气体时，其主要组分和质量分数如表2所示［2］。

表2 底排真实气体主要组分与质量分数Table 2 Main mass fraction of base bleed real gas

2 数值验证

MSTCS-3D已验证过很多经典算例，与参考数值吻合较好，列出其中2个算例来说明该软件的可靠性。

算例一:球头激波诱导燃烧［10－11］。模拟的工况为来流 马 赫 数 是 5.08，静 温 是 291.5 K，速 度 是2 705 m/s，静压是 24 797 Pa，球头半径是 7.5 mm，气体为H2/O2混合物(2H2+O2)，H2-O2反应系统的化学反应模型采用7组分8步基元反应模型。图2和图3为驻点线上压力、温度、主要组分质量分数分布，与参考文献数值模拟结果基本吻合。

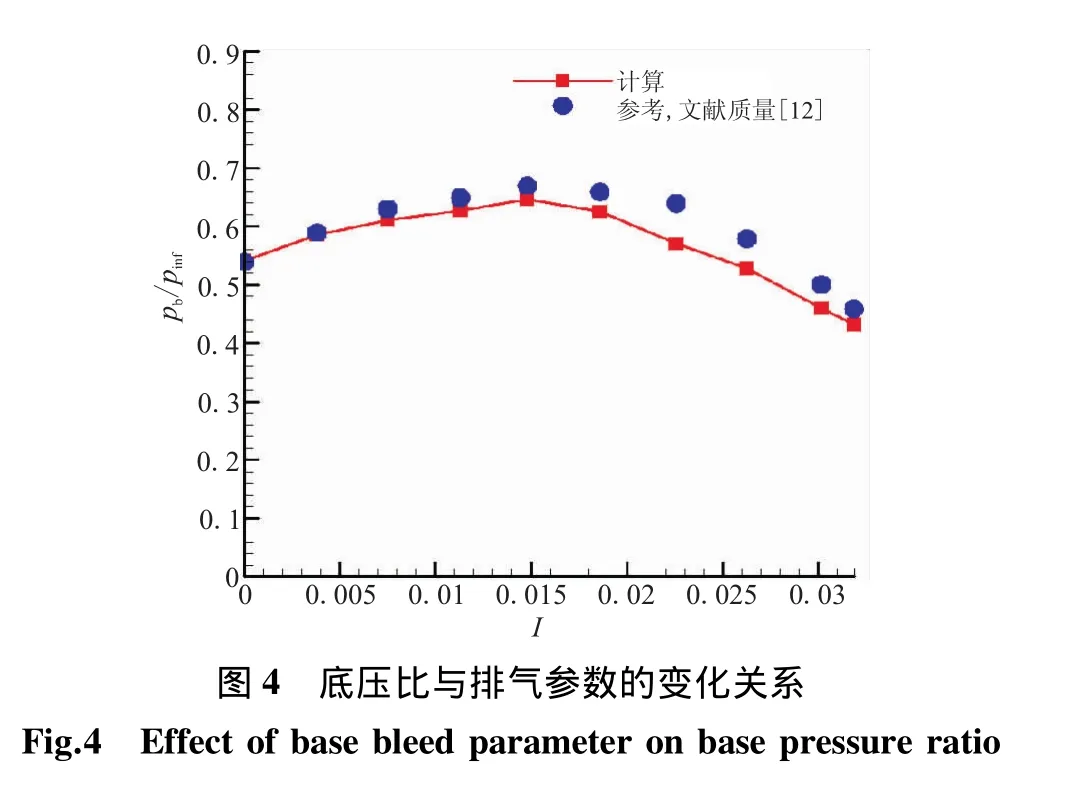
算例二:超声速底部冷排空气实验［12］。来流马赫数2.47，来流总温300 K，底部排气总温293 K，排气介质为空气，排气面积与圆柱体底部面积之比为0.16。计算结果见图4。计算得到的底部平均压力与来流静压之比(简称底压比)随排气参数变化关系与实验结果吻合较好。

3 计算结果与分析

3.1 底排热空气与真实气体的底部流场分析

计算工况为来流马赫数 Ma=3.0，排气参数 I=0.002 2，排气总温T0=1 533 K，进行了底排热空气和底排真实气体的底部流场对比。

图5为底部排热空气/真实气体的底部流线图、温度等值线图(上:热空气;下:真实气体)。

由图5可看出，在相同的来流马赫数、排气总温和排气参数条件下，底排真实气体的流场中前滞止点和后滞止点均比底排热空气中更远离弹底，二次回流区体积也比较大;底部排真实气体流场中二次回流区温度最高，大于底部排气的总温，说明了在该区域发生了化学反应;底部排真实气体的初始回流区温度均高于底排热空气的初始回流区温度。

在相同条件下，底排热空气和底排真实气体所得到底部流场结构和重要参数数值出现较大差别的原因是底排装药气体为富燃气体，排出尾迹区后利用新鲜空气中的氧气，在底部流场中进行掺混和二次燃烧，继续对尾迹区排放热量，通过能量的传输作用，使整个尾迹区温度都升高，流场结构发生局部改变，进而影响底部压力分布。

底部排出的高温富燃气体中H2和CO的量较小，外流空气温度较低，两者接触混合后温度不是很高。因此，在底部流场中发生的化学反应，即二次燃烧是很微弱的，不同于在火箭发动机中高温高压燃烧，二次燃烧不能大幅度提高流场温度，但由于尾流场二次回流区是二次燃烧的主要场所，同时其他区域也存在微弱的化学反应，通过能量的传输，化学反应释放出的热量保证了整个尾流场都具有较高的温度(相比于热排空气)。而在底部排热空气条件下，热空气排出底部后在与来流新鲜冷空气发生传热传质，由于无热源产生，导致底部排出的热空气不断被外流空气冷却，越远离弹底尾，流场温度越低。

图6为底排真实气体时底部流场中H2O的质量分数分布规律。可发现，在二次回流区附近H2O的质量分数最高，且大于底部排气边界的H2O质量分数，结合温度等值线图5(b)中二次回流区的高温区，说明了在二次回流区发生了相对较强的化学反应，它是底部排真实气体二次燃烧的主要场所。这是由于二次回流区是来流空气与底部排出气体强烈混合的地方，且该区域气体流速低，滞留时间较长而更容易发生化学反应。还可看出，在尾迹区越远离弹底，H2O的质量分数越低，这是由于H2O与外流空气不断掺混，单位体积所占质量分数不断降低的结果。

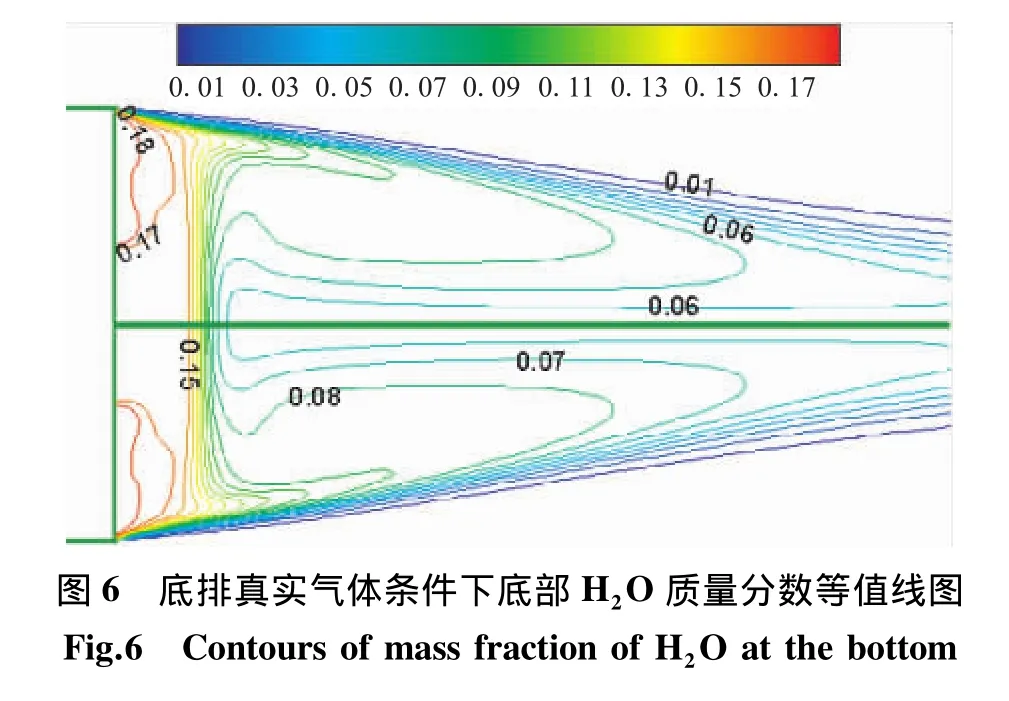
图7为底部湍动能与来流动能的比值等值线图(上:热空气;下:真实气体)。可看出，超声速底部流场中，自由剪切层在再压缩区附近的湍流动能最大;同时，初始回流区与底排气体在中心轴线相遇处湍动能数值也较大，说明了这两个区域的湍流特性最强。

3.2 来流马赫数对底部流场结构与底压比影响规律

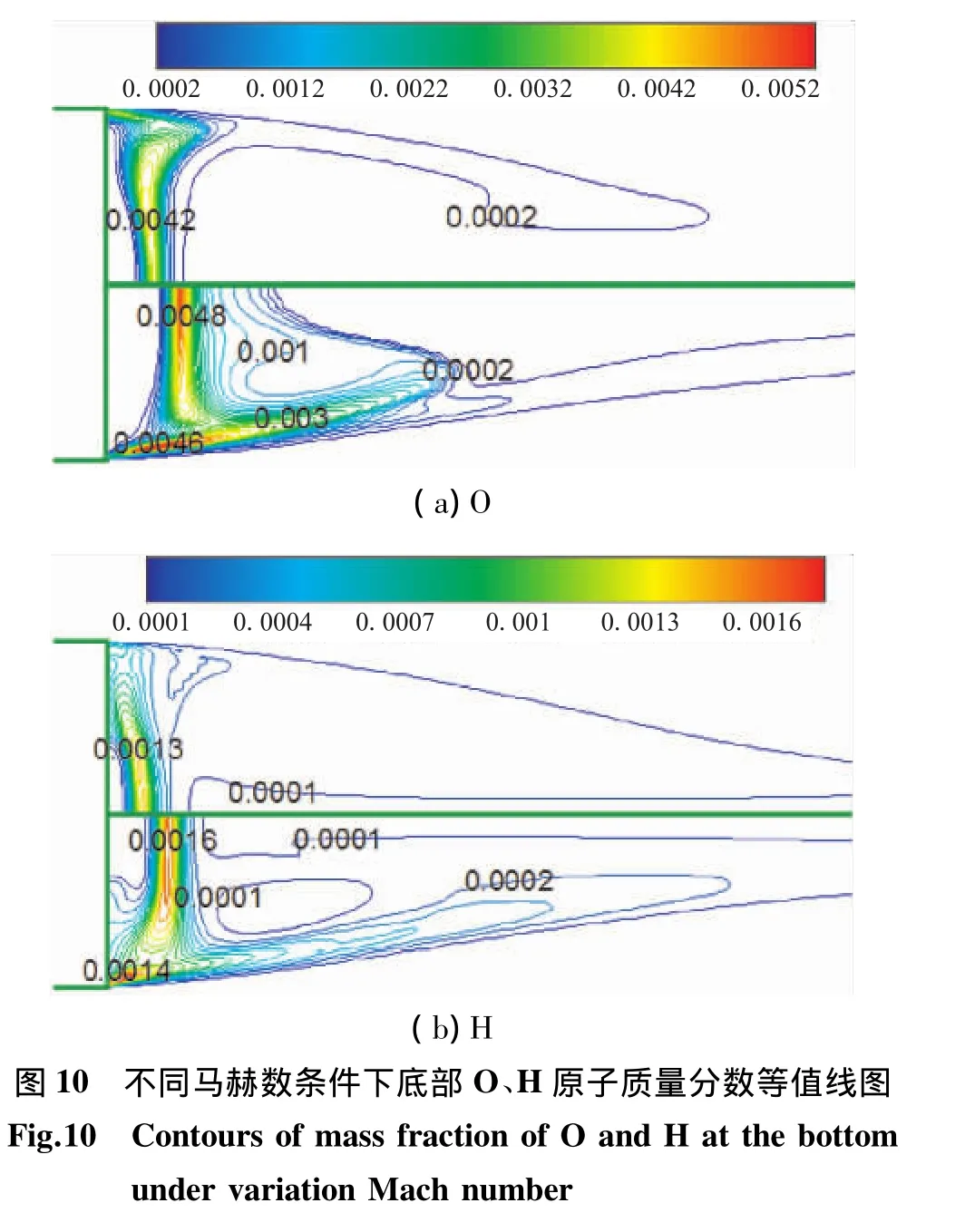
影响弹丸气动特性的重要参数之一是来流马赫数。本节研究了在底排真实气体条件下来流马赫数对底部流场结构和底压的影响。计算了来流马赫数Ma=1.5、2.0、2.5、3.0，排气参数 I=0.002 2，排气总温 T0=1 533 K时的流场。由于篇幅有限，仅列出来流马赫数1.5和3.0时的底部流场结构进行对比。

图8为不同马赫数条件下底部流线和马赫数等值线图(上:Ma=1.5;下:Ma=3.0)。

由于来流马赫数增大，弹丸迎面气流质量流率增大，根据排气参数的定义，若排气参数不变，则弹丸底部排气的质量流率也增大，这就会导致初始回流区向下游移动距离更大，体现在前滞止点的变化;同时，由于初始回流区的后移距离更大，加上弹底固壁的粘性作用，将会在弹底形成二次回流区。

图9为不同马赫数条件下底部温度等值线图(上:Ma=1.5;下:Ma=3.0)。可看出，来流马赫数越大，底部初始回流区的温度均升高，这也是由于来流马赫数的增大，导致排气质量流率的增大，即排出更多具有较高温度的气体与初始回流区相互作用，发生对流和扩散。同时，排出的富燃气体增多，燃料浓度增大，化学反应速率也随之增加，这些都会使底部流场温度升得更高。

图10为不同马赫数条件下底部流场中氧原子、氢原子质量分数等值线图(上:Ma=1.5;下:Ma=3.0)。结合图9、图10可知，底部排出的富燃气体与初始回流区气体在轴线前滞止点附近相遇并混合，而初始回流区的气流主要是外流中的新鲜空气;此时，新鲜空气因与高温富燃气体的混合导致温度大大提高，氧气在第三碰撞体(H2O+H2)作用下开始吸收热量分解成自由基-氧原子，同时氢气也在第三碰撞体(H2O+O2)作用下开始分解成另一自由基-氢原子。此外，底部排出的一部分气体在弹底附近与外流空气的自由剪切层发生传热传质，吸收热量生成自由基-氧原子和氢原子，为后续基元反应(链的分支反应和链传递反应)的发生做准备。由图9和图10(a)可明显看出，在相同排气参数下，随着来流马赫数的增大，底部将排出更多富燃气体，底部流场中链的激活反应越强烈，生成更多的自由基-氢原子和氧原子，这将有利于后续基元反应的进行。由图6的底部H2O质量分数、图9的温度等值线图看出，CO-H2-O2反应系统的后续基元反应主要发生在二次回流区，特别是生成H2O和CO2的基元反应过程中会产生大量的热，从而导致二次回流区温度最高，再通过对流和扩散，提高了初始回流区的温度。

开展底部排气数值模拟最终目的是为了研究减阻特性，而与减阻特性密切相关的参数是弹底压力。图11给出了相同排气参数和排气总温，不同来流马赫数条件下不排气、排热空气、排真实气体的底部平均压力与来流静压之比的分布，表3给出了对应的底部平均压力与来流静压比。当马赫数增大时，无底部排气的弹底压力减小，这是由于来流马赫数增大，自由剪切层在弹底拐点处膨胀角更大，导致底部压力更低。在不同来流马赫数条件下，通过底排热空气或真实气体均能提高底压比，且底排真实气体的提高底部压力比约为底排热空气3倍，如当Ma=3.0时，虽然底部压力较低，但通过底排热空气能提高底部压力比为5.67%，而底排真实气体能提高16.22%。造成底排热空气和真实气体计算的底部压力值出现差异的原因在3.1节已做分析，同时也说明了底部排气热空气和底部排真实气体所得到的减阻效果会有较大差异。由图11和表3还可明显看出，来流马赫数越大，底部排气减阻效果就越显著。因此，工程设计中，尽量考虑在高马赫数飞行阶段下进行排气减阻。

表3 不同来流马赫数条件下底部平均压力与来流静压之比Table 3 Base pressure ratio under variation Mach number

通过以上分析可发现，底排真实气体/底排热空气、来流马赫数对底压的影响主要是通过改变底部复杂流场结构，进而影响底部流场与外流的相互作用来实现的。本文采用的来流参数、排气参数、排气面积比等均与文献［2］相同，计算底排真实气体所得到底部压力分布与文献计算结果基本一致，文献［2］中数值模拟结果也表明，二次燃烧主要发生在二次回流区。这进一步说明了本文计算结果可靠性较高，可将计算软件MSTCS-3D作为用于深入研究底部排气弹减阻机理的工具。

4 结论

(1)计算结果表明，计算软件的数值方法可靠性较高，建立的底部排气弹湍流流动与燃烧模型是正确的，为深入开展超声速底部排气弹底部减阻机理研究打下基础。

(2)底排真实气体效应对超声速流底部减阻模拟有较大影响，采用底排空气进行数值模拟或风洞实验研究底排弹减阻特性时，应慎重对待得到的结论。

(3)底部排气弹底部二次燃烧主要存在弹底流速较低的二次回流区，该区富燃气体与空气充分混合和燃烧，温度较高。

(4)相同排气参数和排气总温条件下，来流马赫数越大，初始回流区后移距离也越大，整个底部流场平均温度也更高。

(5)相同排气参数和排气总温条件下，来流马赫数越大，底部排气减阻效果越显著。

［1］郭锡福.底部排气弹外弹道学［M］.北京:国防工业出版社.1994.

［2］Charles J Nietubica.Navier-stokes computations for a reacting，M864 base bleed projectile［R］.AIAA 93-0504.

［3］Petri Kaurinkoski.Computation of the flow of thermally perfect gas past a supersonic projectile with base bleed［R］.AIAA 96-3451.

［4］Jeong-Yeol Chor.Numerical study of base bleed projectile with external combustion［R］.AIAA 2005-4352.

［5］欧阳水吾，谢中强，徐春光.高温非平衡空气绕流［M］.北京:国防工业出版社，2001:140-142.

［6］Menter F R.Two equation eddy viscosity turbulence models for engineering application［J］.AIAA Journal，1994，32:1598-1605.

［7］周力行.多相湍流反应流体力学［M］.北京:国防工业出版社，2002:185-189.

［8］Steger J L，Warming R F.Flux vector splitting of the inviscid gas-dynamics with application to finite difference methods［J］.Journal of Computational Physics，1981，40(2).

［9］胡湘渝，张德良，姜宗林.气相爆轰基元反应模型数值模拟［J］.空气动力学报，2003，21(1):59-66.

［10］Lehr H F.Experiments on shock-induced combustion［J］.Aerona-utica Acta，1972，17:74-80.

［11］Yungster S，EB Erhardt S.Numerical simulation of hypervelocityp-rojectiles in detonable gases［J］.AIAA Journal，1991，29(2):215-223.

［12］Mathur T，Dutton J C.Base bleed experiments with a cylindrical afterbody in supersonic flow［R］.AIAA 95-0063.