炸药格尼系数的一种简易估算法

沈 飞，王 辉，袁建飞，田清政

（西安近代化学研究所，陕西 西安 710065）

引 言

格尼系数（又称格尼速度）可以反映炸药对金属的加速作功能力，是炸药的一个重要参数。工程上应用格尼系数可以求出炸药对壳体破片加速的最大速度，同时也作为战斗部装药选评的一个重要参考［1－3］。目前，炸药的格尼系数主要通过圆筒试验进行确定，此外，也有一些简易的估算方法，较为典型的是Har desty和Kennedy提出的H＆K算法及Kamlet和Finger提出的 K＆F算法［1，4］。这两种估算方法对于CHNO型炸药的计算误差都较小，但前提是必须知道爆轰产物的成分及摩尔数，而工程上常用的很多高聚物黏结炸药、混合炸药等，其配方成分复杂，很难准确判断出爆轰产物的组成情况，因此无法通过H＆K算法及K＆F算法较为准确地估算出炸药的格尼系数。

在工程实际中，炸药的初始密度及爆速比较容易准确获得，本研究基于圆筒装药结构的格尼模型及炸药爆轰产物的γ律状态方程得出了一种根据炸药密度及爆速估算其格尼系数的方法，并采用该方法对多种炸药的格尼系数进行估算，以检验其准确性。

1 圆筒装药结构的格尼模型

在圆筒装药结构格尼公式的推导过程中，首先假定圆筒为无限长，忽略其作用过程中的端部效应，且圆筒膨胀过程中，整个圆筒壁具有相同的速度［5］。那么，单位长度的圆筒壁所具有的动能为：

式中：Re和Ri分别为圆筒壁外表面和内表面的半径；ρm为圆筒材料的密度；um为圆筒壁的径向膨胀速度；M为单位长度圆筒壁的质量。

对于爆轰产物，假定其具有相同的密度，且径向速度沿半径呈线性分布［5］，即：

则单位长度的炸药产生的爆轰产物所具有的动能为：

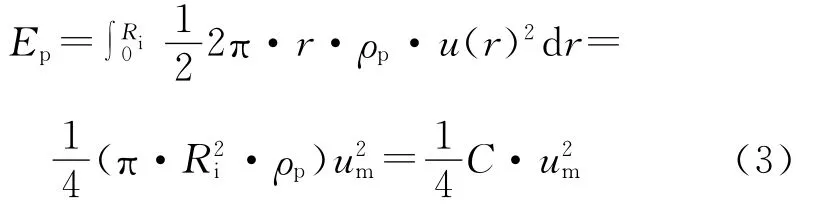
式中：ρp为爆轰产物的密度；C为单位长度炸药的质量。

根据公式（1）和（3），可得出单位质量炸药释放能量转化成的动能为：

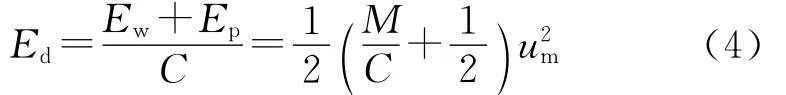
当圆筒壁的膨胀速度几乎不再增加时［6－7］，可将此时的筒壁速度记为uL，且此时的Ed便等于炸药的格尼能Eg，进而可求出该炸药的格尼系数：

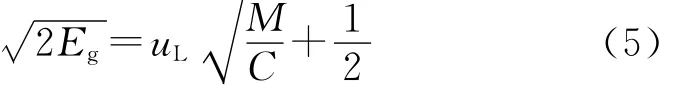
2 简易估算法

2.1 估算法的理论模型

在圆筒膨胀过程中，根据能量守恒关系可认为，随着圆筒壁的膨胀，爆轰产物的内能不断转换成圆筒壁和爆轰产物的动能，即：

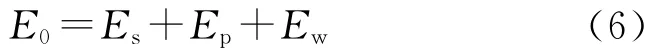
式中：E0为圆筒膨胀初始时刻爆轰产物的内能；Es为膨胀过程中爆轰产物的内能。对于凝聚炸药的爆轰产物，可采用 Grüneisen物态方程［8－9］描述，即：

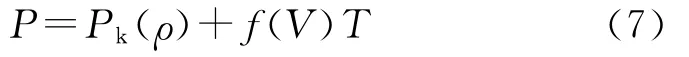
式中：冷压Pk（ρ）取为AV－γ，热压f（V）T＝BT／V，代入式（7）得到：

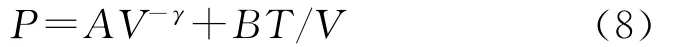
式中：T为温度；P和V分别为爆轰产物的压力和比容；γ为爆轰产物的多方指数；A和B均为与炸药性质有关的常数。对于实际中常用的凝聚炸药，其密度一般大于1.0 g／c m3，爆轰产物中热压对压力的作用相对于冷压要小得多，特别是在爆轰产物膨胀的初始阶段，热压的作用可以忽略［9］，则式（8）可简化为：

式（9）即为爆轰产物的γ律状态方程。

此外，C－J面上的参数有如下关系［8］：

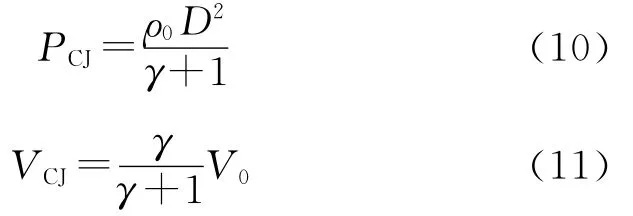
式中：D为炸药的爆速；ρ0和V0分别为炸药的初始密度及比容，ρ0＝1／V0。

根据公式（9）、（10）和（11），可得出：

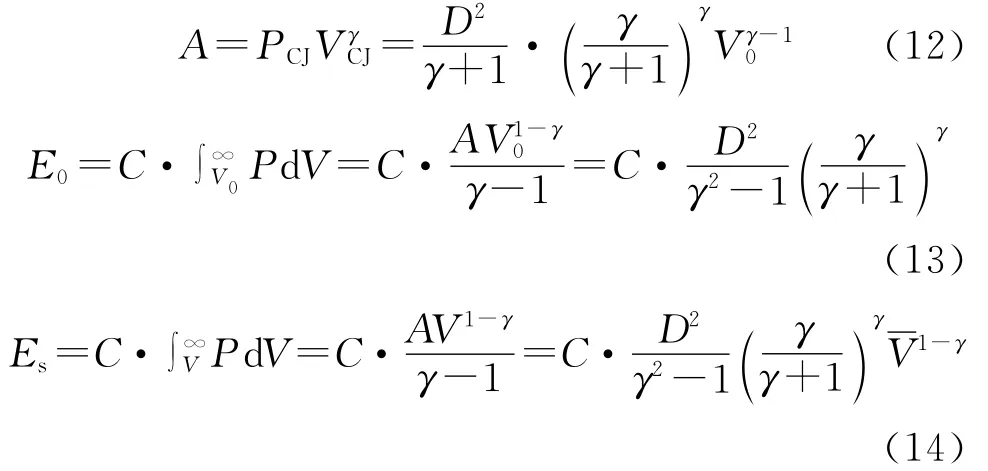
将公式（1）、（3）、（13）和（14）代入式（6），则可得出：

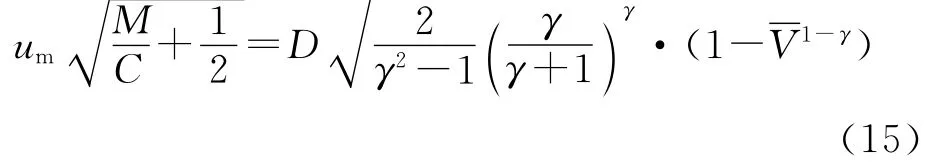
当爆轰产物膨胀到一定程度时，圆筒壁的速度接近最大值，而此时爆轰产物的相对比容V一般都在7.0以上［6－7］，则≈1。那么，由式（5）和（15）可得出：

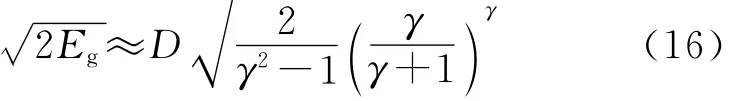
式（16）中多方指数γ是爆轰产物的体积和温度的函数，与炸药的成分和密度相关。有关多方指数γ的计算方法很多，但大部分需要已知爆轰产物的成分及摩尔分数，这对于工程上经常用到的一些混合炸药而言，其计算不方便，可以采用仅需要知道炸药密度便可求出γ的经验公式。本研究对于γ值的计算主要根据Johansson和Persson提出的公式（17），其形式简单，对于密度大于1.0 g／c m3的凝聚炸药具有较好的精度［10］。

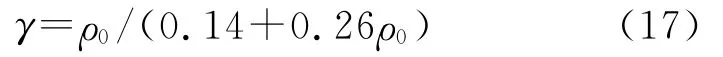
2.2 算 例

选择部分已知密度和爆速的炸药，采用公式（16）和（17）计算其格尼系数，并与实验值进行对比，结果如表1和表2所示。其中，表1中所列的格尼系数实验值均来自文献［11］，表2中所列格尼系数实验值是将文献［12］中Φ25 mm圆筒试验值代入式（5）得到的。计算过程中，取圆筒壁膨胀距离为19 mm时（此时爆轰产物相对比容约为7）圆筒壁的膨胀速度作为uL。从表1和表2可以看出，格尼系数的计算值与实验值相差较小。

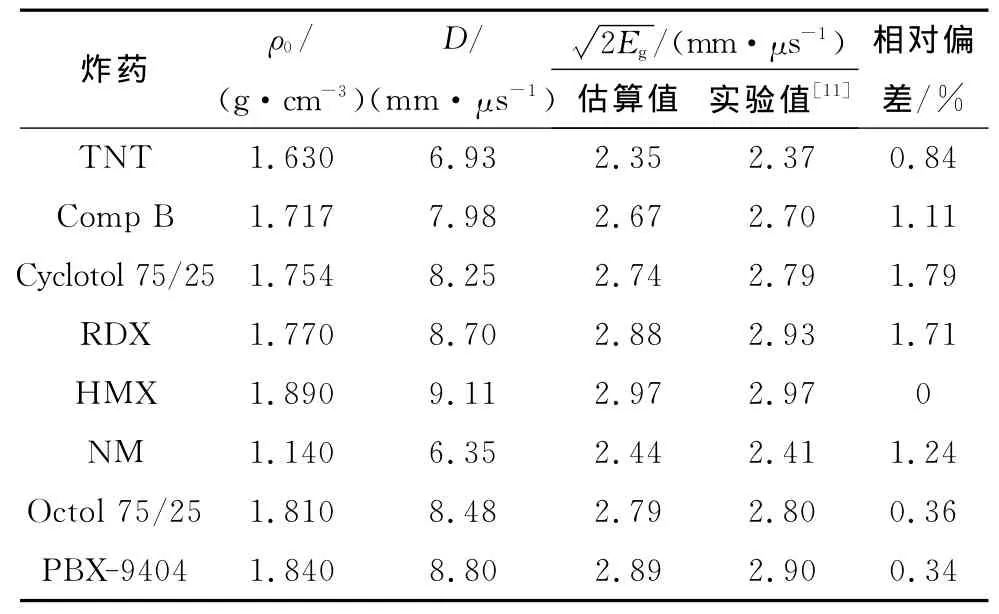
表1 炸药格尼系数的估算值与文献值的对比Table 1 Co mparison of calculated Gur ney coefficient with literature one

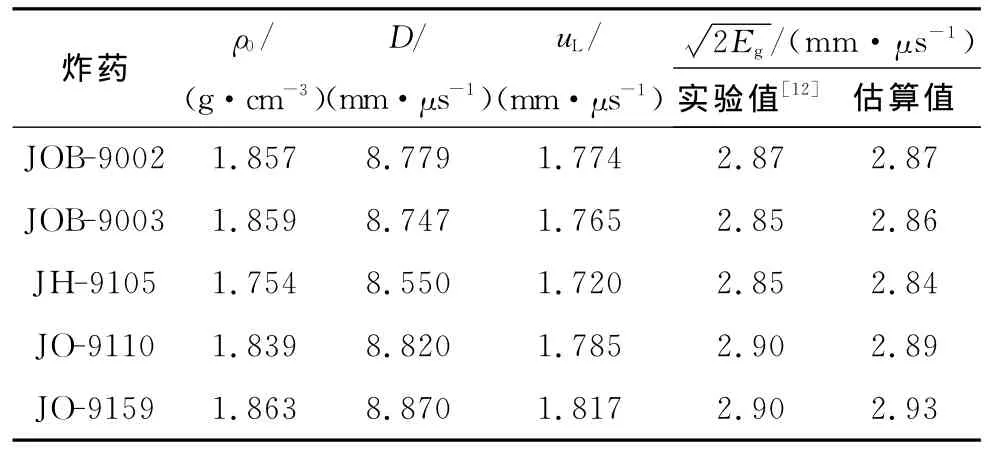
表2 格尼系数的估算值与Φ25 mm圆筒试验值的对比Table 2 Co mparison of calculated Gur ney coefficient with values measured fr o mΦ25 mm cylinder test

3 结 论

（1）基于圆筒装药结构的格尼模型及凝聚炸药爆轰产物的γ律状态方程推导出了炸药的格尼系数关于

（2）该方法对于密度大于1.0 g／c m3的凝聚炸药具有较好的精度，能够满足工程应用的需要。

［1］ 孙业斌，惠君明，曹欣茂.军用混合炸药［M］.北京：兵器工业出版社，1995.

［2］ 韩秀凤，严楠，蔡瑞娇.对炸药驱动飞片速度的理论计算方法的分析与评价［J］.火炸药学报，2005，28（1）：63－66.HAN Xiu－feng，YAN Nan，CAI Rui－jiao.Analysis and assess ment on theoretical calculation methods for the velocity of explosive－driven flyer plate［J］.Chinese Journal of Explosives and Propellants，2005，28（1）：63－66.

［3］ Wang M F，Lu F Y，Li X Y，et al.A for mula for calculating the velocities of frag ments from velocity enhanced war head［J］.Propellants，Explosives，Pyr otechnics，2013，38：232－237.

［4］ Keshavarz M H.An alter native method for esti mation Gurney velocity based on assumed detonation products［J］.Chinese Jour nal of Ener getic Materials，2006，14（6）：499－452.

［5］ Walters W P，Zukas J A.Fundamentals of Shaped Charges［M］.Canada：John Wiley ＆Sons，1989.

［6］ Hornberg H，Volk F.The cylinder test in the context of physical detonation measurement methods［J］.Propellants，Explosives，Pyrotechnics，1989，14：199－211.

［7］ Souers P C，Lauderbach L，Garza R，et al.Upgraded analytical model of the cylinder test［J］.Pr opellants，Explosives，Pyrotechnics，2013，38：419－424.

［8］ 奥尔连科 ЛП.爆炸物理学（上册）［M］.孙承纬，译.北京：科学出版社，2011.

［9］ 孙承纬，卫玉章，周之奎.应用爆轰物理［M］.北京：国防工业出版社，2000.

［10］Johansson C H，Persson P.Density and pressure in the Chap man Jouguet Plane as f unctions of initial density of explosive［J］.Nature，1966，212：1230－1231.

［11］Dobratz B M，Crawford P C.LLNL Explosives Handbook，Properties of chemical explosives and explosives si mulants，Report UCRL－52997［R］.Lawrence：Liver more National Laboratory，1985.

［12］董海山，周芬芬.高能炸药及相关物性能［M］.北京：科学出版社，1989.