石墨含量和粒度对RDX／石墨混合炸药爆速的影响

曹 渊，仝 毅，黄风雷

（北京理工大学爆炸科学与技术国家重点实验室，北京100081）

引 言

混合炸药爆轰性能的研究一直是炸药领域的研究重点。赵雪等［1］研究了RDX 颗粒形态对RDX基熔铸炸药性能的影响，提出通过改变单质炸药的颗粒形态来提高炸药的装药性能；刘意等［2］对加入高密度惰性金属颗粒的非均质炸药爆轰传播过程进行了数值模拟研究，得到了金属颗粒间隙大小对爆轰传播的影响规律和可能导致装药熄爆的炸药与金属的临界质量配比；苗勤书等［3］研究了铝粉粒度和形状对含铝炸药性能的影响，应用含铝炸药的二次反应理论和惰性热稀释理论解释了铝粉形状和粒度对炸药性能的影响机理，认为其原因是由于铝粉比表面积不同造成的；王玮等［4］研究了装药密度及尺寸对RDX 基含铝炸药爆压和爆速的影响，拟合出了爆压、爆速与装药密度的关系式。

RDX／石墨混合炸药是爆轰合成聚晶金刚石的主要原料，准确测量其爆轰性能可以为聚晶金刚石爆轰合成的机理研究提供重要实验依据。炸药爆速是目前唯一用比较简单的方法能准确测量的参数，也是衡量其他爆轰参数的重要依据。本研究通过测试RDX／石墨混合炸药的爆速，分析了石墨含量和粒度影响RDX／石墨混合炸药爆速的机理，结合爆速ω-Г余容公式，提出了计算公式，为人工合成聚晶金刚石及其他相关领域的研究提供参考。

1 实 验

1.1 材 料

石墨，化学纯，粒度分别为48、20、10、4.5μm，北京化学试剂公司；RDX，Ⅰ类2型，甘肃银光化学工业集团有限公司。

1.2 爆速测试装置

爆速测试装置由起爆电源、雷管、药柱、双丝式探针、脉冲形成网络、电缆和数字示波器组成，如图1所示。其原理为［5］：当爆轰波到达安装有双丝式探极的区域时，由于爆炸产物的导电性使探极接通，探极的开关状态突变使脉冲形成网络产生电压脉冲信号，脉冲信号经传输线由计时器记录下来。实验测试炸药为圆柱形压装RDX／石墨混合炸药，为保证测试时药柱达到稳定爆轰状态，传爆药柱的尺寸为Ф40mm×60mm，且一端带雷管孔，测试药柱尺寸为Ф40mm×20mm，实际长度以装配时的测量尺寸为准（取四次测量的平均值），整体药柱的密度为所有小药柱密度的平均值。所有实验均采用5个电探针，将第一个触发探针作为时刻零点和位置零点，可以得到4个时间点和相应的4个位置点，对所得数据用Origin软件进行线性拟合，所得斜率即为爆速值。

图1 爆速测试实验装置示意图Fig.1 Diagrammatic sketch of experiment setup for testing detonation velocity

1.3 ω-Г 余容公式

计算混合炸药爆速的经验和半经验公式主要有Kamlet公式、Urizar公式、ω-Г余容公式等。ω-Г余容公式对RDX／石墨混合炸药爆速的计算结果与实测结果误差相对较小［6-7］，计算式为：

式中：Q为混合炸药的爆热（J／g）；ω为位能因子［8］；ρ0为装药密度（g／cm3）；Qi为组分i的爆热（J／g），Qi（RDX）=5 790（J／g）、Qi（石墨）=0（J／g）；ωi为组分i的位能因子，ωi（RDX）=14.23、ωi（石墨）=3.83；wi为混合炸药中组分i的质量分数。

ω-Г余容公式在计算爆速时分为两项：第一项是炸药爆轰反应释放的能量对爆速的贡献；第二项243是反应后爆轰产物所具有的势能对爆速的贡献。ω-Г余容公式对于单质炸药的计算精度很高［9］，加入惰性物质石墨后，计算精度降低。

2 结果与讨论

2.1 石墨含量和粒度对爆速的影响

RDX／石墨混合炸药实验测试结果Dexp和ω-Г余容公式计算结果Dcal见表1。

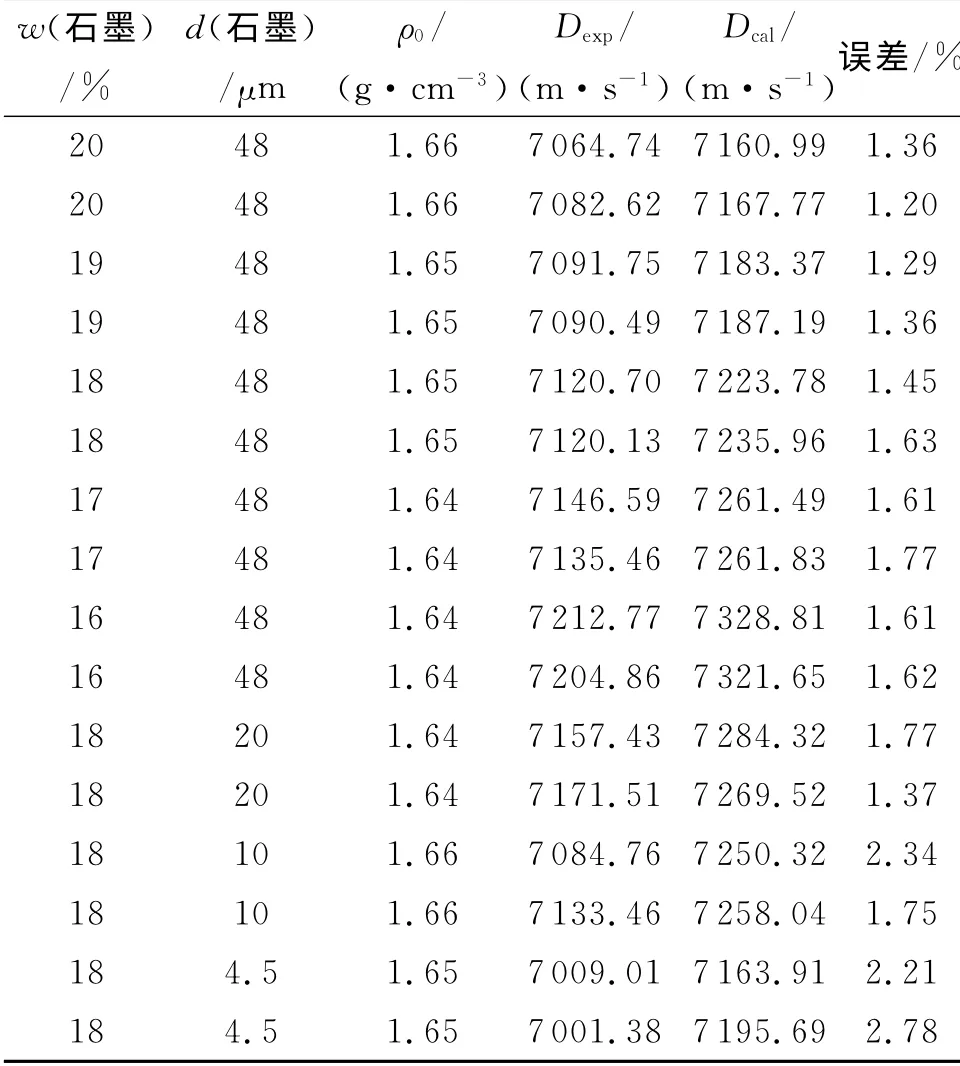
表1 RDX／石墨混合炸药的爆速测试和计算结果Table 1 Test and calculated results of detonation velocity of RDX／graphite mixed explosive

由表1可以看出，当石墨的粒度为48μm 时，混合炸药的爆速随着石墨含量的减少逐渐增大；当石墨的质量分数为18%时，爆速随着石墨粒度的减小逐渐降低。

由于RDX 是接近零氧平衡的负氧炸药，爆轰反应的时间小于0.1μs［10］，石墨发生氧化反应的时间要远远滞后，所以在爆轰波阵面上，可以认为石墨不参与爆轰反应，而是作为惰性介质吸收RDX反应释放的能量。吸收能量的方式有两种：作功和热传递。文献［7］中给出了石墨的位能因子ω=3.83，代表石墨被压缩作功后所具有的势能；而Q=0意味着在爆轰波阵面上石墨处于绝热状态。忽略热交换，该公式的工程应用是合理的，当深入研究石墨对爆轰过程的影响时必须考虑其吸热效应。综上分析可以认为，未计算石墨颗粒在爆轰波阵面上通过热传递吸收的能量是余容公式对RDX／石墨混合炸药计算误差的主要来源，使得计算结果偏大。

由表1中石墨含量与误差的变化关系，并结合极限思想可知：石墨含量为零时，吸热造成的误差为零；石墨含量很小时，在波阵面上吸热量很小，误差很小；随着石墨含量增加，吸收的热量增加，误差增大；石墨含量继续增加，吸收的热量减小，误差又逐渐降低。影响石墨吸热量的主要因素有两个：一是石墨的含量，单位质量混合炸药中吸收能量的惰性介质越多，吸能就越多；二是石墨和爆轰产物的温差，影响热量传递的速率和大小，对于RDX／石墨混合炸药，RDX 含量越高，单位质量混合炸药反应释放的能量越多，爆温越高，温差越大，石墨吸收热量就越多。因此，石墨粒度不变的条件下，石墨含量和RDX 含量共同决定石墨在爆轰波阵面上吸收热量的大小。

由表1中石墨粒度与误差的变化关系，并结合前人的研究［3，9］可知，石墨含量相同时，随着石墨的粒度减小，比表面积增大，吸收的热量增大，误差逐渐增大。当石墨粒度减小到微、纳米量级时，热导率降低［11］，也会影响热传递速度。根据热导率的德拜表达式（K=1／3·CV·L），影响热导率的主要因素是声子的平均自由程L。平均自由程L的大小由两个散射过程决定：声子间碰撞引起的散射，以及声子与晶体的晶界、各种缺陷、杂质作用引起的散射。当传热现象发生在微／纳尺度时，包括微秒或纳秒量级的时间尺度和微米或纳米量级的空间尺度，由于传热过程发生的时间很快、空间尺度微小，达到甚至小于载热粒子的弛豫时间或平均自由程的量级，其过程具有不同于大尺度的特殊规律，载热构件也表现出迥异于大体积材料的特殊的热学性质。石墨材料的热传导主要由声子进行，影响其热导率的主要因素是声子的平均自由程。当石墨颗粒尺寸小到可以和声子的平均自由程相比拟的时候，相对于声子之间的碰撞，声子将更多地在界面处发生散射，声子的平均自由程将受到限制，从而降低了热流的传输。当尺寸很大时，声子运动的平均自由程基本不再受到界面的影响，热导率也将趋于稳定。因此，石墨含量不变的条件下，石墨粒度变化引起比表面积和导热率的变化，二者共同影响石墨吸收热量的大小。

2.2 爆速ω-Г 余容公式的修正

综合上述分析，影响石墨吸收热量的因素为：单位质量混合炸药中石墨的质量分数、RDX 的质量分数、石墨的导热率以及比表面积。球形颗粒的比表面积与半径成反比，但石墨颗粒为不规则片状，比表面积与颗粒的粒度关系需要修正，提出特征尺寸dl，d为惰性物颗粒的粒度，l为粒度修正系数。修正公式为：

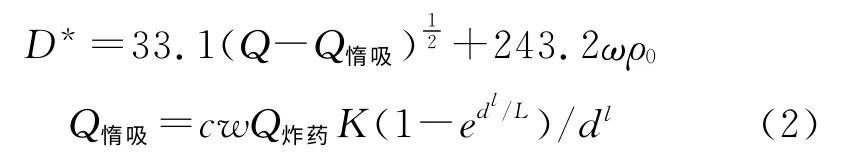
式中：D＊为修正后的爆速（m／s）；K为惰性物常温导热率（W·m-1·K-1）；L为惰性物常温的声子平均自由程（μm）；Q炸药为单位质量混合炸药中RDX的爆热（J／g）；w为惰性物质量分数；d为惰性物颗粒的粒度；l为粒度修正系数，0.2；c为拟合常数，0.0083。

对于石墨，K=129W · m-1· K-1，L=0.5μm。通过公式（2）计算得到修正后炸药爆速与石墨含量及粒度的关系，结果见图2。公式（2）可精确预测RDX／石墨混合炸药的爆速，经计算误差绝对值的平均值由原公式的1.68%减小到修正后的0.24%。

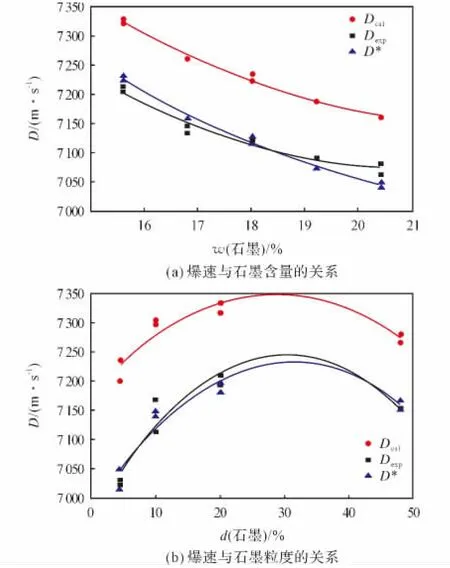
图2 实验、ω-Г 余容公式和修正公式爆速结果比较Fig.2 Comparison of detonation velocity obtained by experiment，theω-Гcovolume formula and the amended formula

为验证公式的适用性，计算了两相混合炸药的爆速。根据含铝炸药的二次反应理论和惰性稀释理论，认为铝粉在波阵面上一般不参与反应，而且还要吸热，使波阵面上用于支持爆轰的能量减小，改变铝粉的含量和粒度大小，同样对爆速产生影响［3，12］。

表2中含铝炸药所用铝颗粒为片状［3］，与石墨颗粒形状近似，因此粒度修正系数d和拟合常数与石墨取值相同。常温下，铝的导热率K=237W／（m·K），CV=880J／（kg·K），由导热率与比热容之间的关系式（3）：

可计算出L=0.85μm。

根据式（2）计算，修正公式对于含铝炸药爆速的计算结果与ω-Г余容公式相比，误差分别减小了3.36%、3.67%。但由于铝粉形状与石墨颗粒的差异、装药密度的不同以及含铝炸药爆轰反应的复杂性，继续提高含铝炸药爆速的计算精度，需要相同铝颗粒形状条件下更多的实验测试数据，对粒度修正系数l和拟合常数c作进一步的修正。

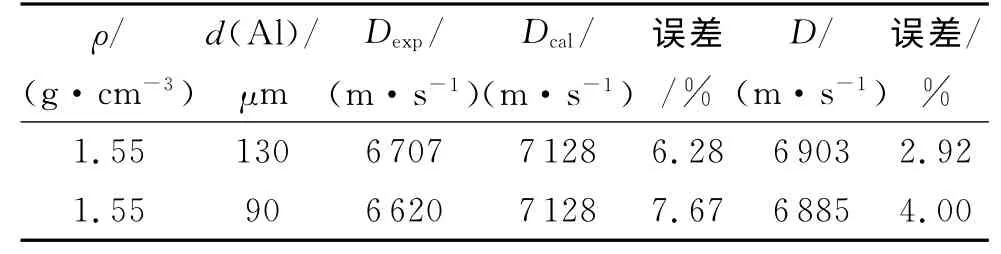
表2 RDX／Al混合炸药爆速的实验结果和计算结果Table 2 Test and calculated results of detonation velocity for RDX／Al mixed explosive

3 结 论

（1）石墨和RDX 的含量共同影响了RDX／石墨混合炸药中石墨在波阵面上吸热量的大小，随着石墨含量的增加，吸热量先增大后减小。

（2）随着石墨粒度的减小，比表面积增大，吸热量增大。

（3）基于RDX／石墨混合炸药的爆速实验数据，得到改进爆速修正公式，提高了该混合炸药爆速计算的精度，使得计算值与实验值的平均误差由1.68%减小到0.24%。

［1］赵雪，芮久后，冯顺山.RDX 颗粒形态对RDX 基熔铸炸药性能的影响［J］.南京理工大学学报，2011，35（5）：714-716.

ZHAO Xue，RUI Jiu-hou，FENG Shun-shan.Effects of RDX physical morphology on properties of RDX base melt-cast explosive［J］.Journal of Nanjing University of Science and Technology，2011，35（5）：714-716.

［2］刘意，王仲琦，白春华，等.惰性金属颗粒炸药中爆轰传播数值模拟研究［J］.兵工学报，2009，30（2）：66-73.

LIU Yi，WANG Zhong-qi，BAI Chun-hua，et al.Numerical simulation of detonation propagation in inert metal particle explosive［J］.ACTA Armamentarii，2009，30（2）：66-73.

［3］苗勤书，徐更光，王廷增.铝粉粒度和形状对含铝炸药性能的影响［J］.火炸药学报，2002，25（2）：4-8.

MIAO Qin-shu，XU Geng-guang，WANG Ting-zeng.Mechanism analysis of the influence of Al shape and size on the detonation properties of aluminized explosives［J］.Chinese Journal of Explosives and Propellants，2002，25（2）：4-8.

［4］王玮，王建灵，郭炜，等.装药密度及尺寸对RDX 基含铝炸药爆压爆速的影响［J］.含能材料，2010，18（5）：563-567.

WANG Wei，WANG Jian-ling，GUO Wei，et al.Effect of charge density and size on detonation pressure and detonation velocity of RDX-based aluminized explosive［J］.Chinese Journal of Energetic Materials，2010，18（5）：563-567.

［5］黄正平.爆炸与冲击电测技术［M］.北京：国防工业出版社，2006：84-94.

［6］赵迎春.石墨对TNT、RDX 机械感度和爆轰性能影响的研究［D］.北京：北京理工大学，2011.

ZHAO Ying-chun.Research on effect of graphite on mechanical sensitivity and detonation properties of TNT and RDX［D］.Beijing：Beijing Institute of Technology，2011.

［7］WU Xiong.A simple method for calculating detonation parameters of explosives［J］.Journal of Energetic Materials，1985（3）：263-277.

［8］Charles L M.Numerical Modeling of Explosives and Propellants［M］.New York：CRC Press，2007.

［9］郑孟菊，俞统昌，张银亮.炸药的性能与测试技术［M］.北京：兵器工业出版社，1990：122-123.

［10］张宝坪，张庆明，黄风雷.爆轰物理学［M］.北京：兵器工业出版社，2001：152-153.

［11］李红梅.石墨薄膜热导率的研究［D］.苏州：苏州大学，2010.

LI Hong-mei.Study of thermal conductivity of graphite films［D］.Suzhou：Soochow University，2010.

［12］孙业斌，惠君明，曹欣茂.军用混合炸药［M］.北京：兵器工业出版社，1995.