基于悬链线理论的雷达高架索梁系统结构分析
2013-09-16杜春江瞿亦峰
杜春江,瞿亦峰
(南京电子技术研究所, 江苏 南京 210039)
基于悬链线理论的雷达高架索梁系统结构分析
杜春江,瞿亦峰
(南京电子技术研究所, 江苏 南京 210039)
针对目前雷达高架结构采用ANSYS软件计算中对拉索模型简化不合理造成的计算精度低的问题,提出了基于悬链线理论的高架拉索结构分析解决方案,并编制了拉索结构分析程序,采用典型算例证明了该程序的有效性。对不同拉索垂度情况下典型的两拉索高架结构的静态变形进行了分析,并对计算结果进行了校核。结果表明,该方法可以实现考虑拉索垂度效应的索梁系统的精确分析。
高架结构;悬链线;拉索
引 言
拉索广泛应用于雷达高架结构中,可以增强系统整体刚度,减小顶端位移量和偏转角度,提高系统精度。对拉索结构的分析目前主要有以下几种形式:两节点直线法、利用等效弹性模量法修正的两节点直杆法、两节点抛物线单元法、多节点等参索单元法和两节点悬链线单元法[1]。相对于两节点悬链线单元法,其他方法由于都采用了简化计算,无法实现对拉索自重垂度引起的非线性力学行为的精确分析。并且目前多数有限元分析软件(如ANSYS)中普遍把拉索简化为两节点直线杆单元,对于拉索尚缺乏精确的建模,没有考虑由垂度造成的几何非线性问题,从而造成高架系统整体刚度计算不准确和难以确定拉索初始长度,为结构设计带来一定的风险和难度。
针对以上问题,本文基于悬链线理论建立拉索分析模型,编制了拉索受力计算程序,以典型算例验证了该程序的有效性,对考虑和未考虑垂度效应的计算精度进行了简单对比。进而建立了典型的两拉索梁系统分析模型,将拉索受力加载于高架索梁受力处,通过迭代计算使索梁系统的力与位移收敛,实现索梁系统的分析。采用商用有限元分析软件ANSYS验证了计算结果,为雷达高架结构索梁系统的精确设计提供了参考。
1 基于悬链线拉索的基本理论及拉索分析方法
索结构的主要优点是能够承受巨大的拉力,充分发挥高强度钢丝抗拉强度大、可缠绕收拢等特点,因而在高机动高架系统中得到了广泛应用。索结构发生的变形包括两部分:一是材料应变引起的弹性变形;二是索自重引起的几何形状的改变,即自重垂曲。材料在弹性工作状态下,弹性变形与索所受的张力成线性关系,但自重垂曲与索力成非线性关系,这就使索的张力
与变形成非线性关系。
图1为位于铅垂面内的一弹性悬链线单元。设索段无应力长度为s0,抗拉刚度为EA(材料等效的弹性模量与索等效横截面积的乘积),单位索长自重为q,支点A的坐标为(xi,yi),支点B的坐标为(xj,yj),索力在水平方向的分力为H,垂直方向的分力为V,两端点A、B间的水平间距和垂直间距分别为l和h。

图1 悬链线单元示意图
为简化索结构模型和计算方法,作如下假设:
1)索段为线弹性材料,其应力应变关系满足胡克定律;
2)索段是理想柔性的,只能承受拉力,不能受压和抗弯;
3)不考虑索段横截面积在变形前后的变化,即计算索段弹性伸长时不考虑索段抗拉刚度的变化及单位索长自重的变化。
则根据悬链线方程可以获得:
(1)
(2)
其中:
Hi=-Hj;Vi=qs0-Vj;

从式中可以看出,一个索段有3个独立的未知量,因此,只要Hi、Vi和l已知,就可求出s0和h;同样,如果l、h和s0已知,就可求出Hi和Vi。
图2为一悬链线单元索力与索形变化关系的典型算例。采用无量纲计算技术,索的无应力长度为100,抗拉刚度EA为3×107,单位索长自重为1。在Matlab中编程计算的结果与文献[2-3]对比如表1所示。

图2 悬链线单元索力与索形变化关系

点编号点坐标XY本文计算结果FxFy文献[2-3]计算结果FxFy120303.0619.933.06119.93240309.1719.249.17219.243603022.1515.7322.1515.7348030504.1-328.86504.0-328.85100304255727.78-2553384.86417×104-2511×103
从表1可以看出,本文程序的计算结果与文献[2-3]中的计算结果基本一致,从而验证了本文索力计算程序的有效性。
对于该算例,若采用通常的ANSYS建模方式,直接在两点之间做一直线来模拟拉索,则当索下端由(60, 30)移动到(80, 30)时,索的长度由84.85变化到100,伸长量为15.15,计算出的索力为0.54×107,X和Y向索力分别为0.43×107和0.32×107,与抛物线法和悬链线法计算结果相差非常大。因此在垂度较大的情况下,采用ANSYS中的直线索元来模拟拉索其计算精度存在问题,垂度越大精度越低。为此本文编制了基于悬链线理论的索力和索形关系计算程序。
2 典型两拉索高架结构静力学分析
采用编制的索力计算程序对典型的两拉索高架结构进行静力学分析。索的基本参数如下:初始长度Lu=25 100 mm,弹性模量为200 000 MPa,有效横截面积为1 256 mm2,单位索长自重ρ=0.096 N/mm,索端间距如图3所示。高架系统等效转化后梁结构横截面参数为600 mm × 600 mm,壁厚5 mm。在梁的顶端分别施加载荷Fx=-10 000 N,Fy=-100 N,梁的底端约束全部自由度。
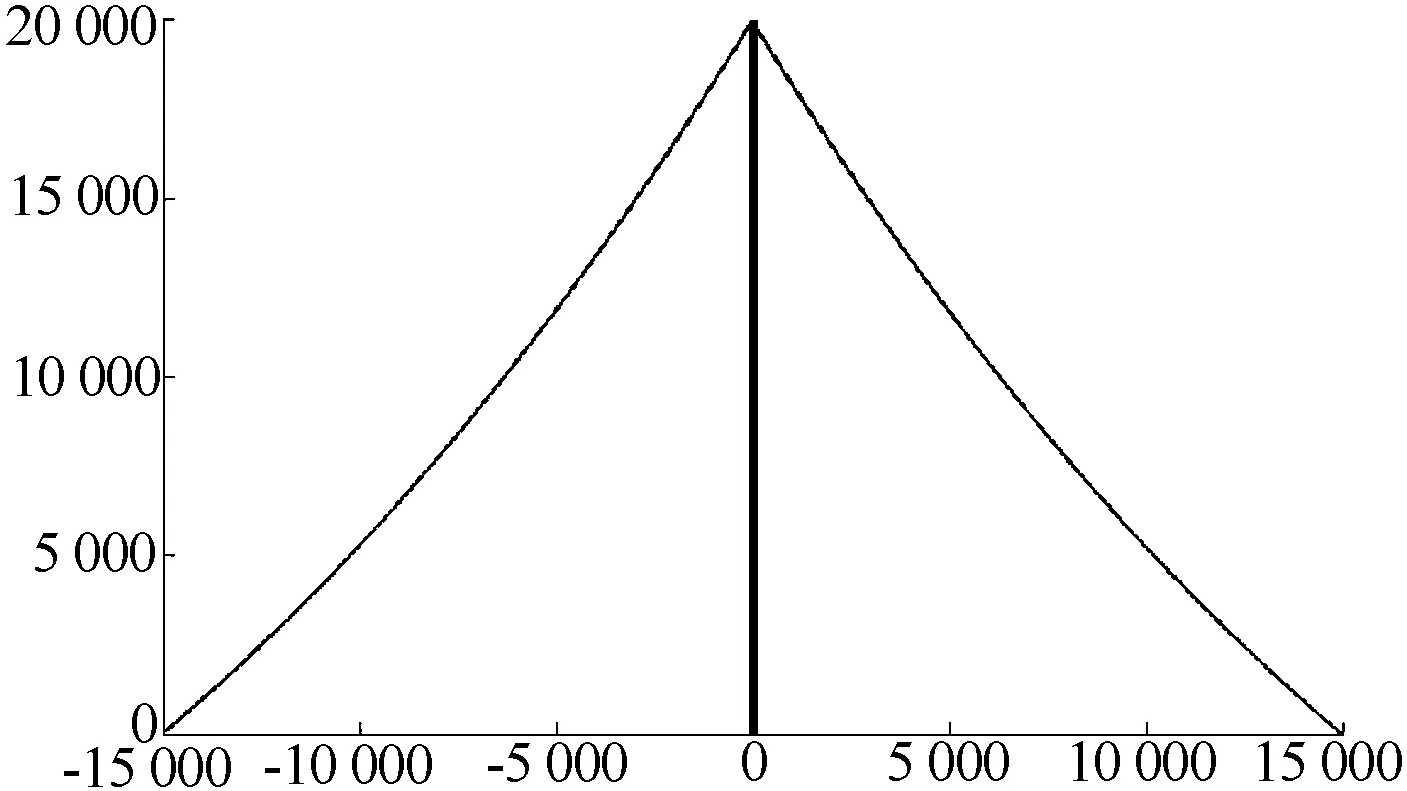
图3 两拉索梁系统模型
两拉索高架结构的静力学分析基本步骤如下:
1)单独计算高架结构在外载荷Fx和Fy作用下的变形Ux和Uy;
2)单独计算左、右两拉索在高架结构位移Ux和Uy后产生的索端载荷Fx1、Fy1、Fx2和Fy2;
3)将Fx1+Fx2+Fx和Fy1+Fy2+Fy-2Luρ施加在高架结构顶端,并重新计算高架结构变形Ux和Uy;
4)重复步骤2获得索端载荷Fx1′、Fy1′、Fx2′和Fy2′,并计算ΔF1=Fx1-Fx1′,ΔF2=Fx2-Fx2′;
5)重复2、3、4,直到ΔF1≤0.01 N、ΔF2≤0.01 N,即认为索梁系统达到平衡状态。
计算后梁顶端水平方向位移-150.6 mm,竖直方向位移-0.17 mm,索梁系统最终变形如图4所示(变形量相对较小,因此变化不明显)。

图4 两拉索梁系统变形
为验证以上计算结果的有效性,使用ANSYS对计算结果进行了校核。
不考虑梁的情况下,当两拉索顶端发生水平方向位移-167.75 mm、竖直方向位移-0.123 7 mm时,两端拉索产生相应拉力。因此单独对梁而言,加载在梁顶端的载荷:
Fx=4 257.15-2 209.6-10 000=-7 952.4 N
Fy= -1 862.9-4 490.1-100-2×25 100×0.096=
-11 272.2 N
将以上载荷单独施加在无索梁单元上,计算获得的梁顶端水平方向位移为-150.6mm,竖直方向位移为-0.17mm。从以上分析可以看出,索梁结构在外载荷作用下发生变形,达到某一稳态后索力与位移一致,可以认定索力计算程序的有效性。
为了验证该程序同样能够保证大垂度索梁系统的计算精度,将上例索的初始长度更改为27 000mm(图5),边界条件和载荷均与原来相同。计算获得的梁顶
端水平方向位移为-1 464.97mm,竖直方向位移为-0.165mm,索梁系统最终变形如图6所示。采用同样方法对该算例进行了校核。

图5 27 m初始索长两拉索梁系统模型

图6 27 m初始索长两拉索梁系统变形
从以上两个算例的计算结果可以看出,本文的索梁系统计算方法可以精确有效地对不同垂度拉索的静态力学性能进行分析。
3 结束语
本文指出了目前高架结构索元建模中存在的问题;编制了基于悬链线理论的拉索系统索力和索形关系计算程序,典型算例的计算结果表明该程序可以模拟任意垂度的拉索;进行了典型两拉索高架结构的计算和校核,结果表明该程序可以解决索的非线性导致的计算误差大的问题。
[1] 彭卫, 孙柄楠, 唐锦春. 一种用于索结构分析的悬链线单元[J]. 应用力学和数学, 1999, 20(5): 504-506.
[2] 梁立农, 韩大建. 索的非线性有限元与调索方法研究[J]. 工程力学, 2007, 24(11): 146-152.
[3]MaxIrvineH.Cablestructures[M].London:MITPress, 1981.
杜春江(1979-),男,高级工程师,主要研究方向为机械设计、机械系统仿真。
Analysis of Cable Structure of Radar High Tower Based on Catenary Theory
DU Chun-jiang,QU Yi-feng
(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)
To solve the low accuracy problem caused by the unreasonable simplification of cable model in the ANSYS computation for radar high tower structure, the cable structure analysis solution based on catenary theory is proposed. Cable structure analysis program is given and typical instance computation verifies the effectiveness of the program. The static deformation of typical two cable high tower structure under different cablesag is analyzed, and the result is verified using ANSYS. Result shows that the method can realize accurate analysis of cable-beam structure with cable sag considered.
high tower structure; catenary; cable
2013-09-11
TN957.8
A
1008-5300(2013)06-0045-03
