一种测量斜拉桥拉索索力新方法——垂度法

葛俊颖，苏木标，李文平

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 大型结构健康诊断与控制研究所，河北 石家庄 050043)

目前斜拉桥索力的测试方法主要有液压表法、测索伸长量法、压力传感器法、磁通量法和振动频率法等[1-2]。液压表法和测索伸长量法一般仅用于拉索张拉施工过程中的索力测量，无法测量已张拉完毕的拉索。压力传感器法由于压力传感器的售价昂贵、自身重量大，需在施工阶段预先埋置，而且输出的结果存在漂移，因而限制了这种方法在索力检测和长期监测中的应用。磁通量法需要事先测定拉索材料特性并在拉索内放置小型电磁传感器[1]，才可用于测量施工过程中和成桥的索力，但要求初期投入成本较高，国外应用较多而国内应用相对较少。振动频率法因其操作方便且成本相对低廉是目前成桥索力测量中应用最广泛的方法[3-5]，但该方法的测试结果准确程度非常依赖测试者的经验，并受到索长、两端约束、索的抗弯刚度和垂度以及其他外部因素的影响[1, 3]。另外，三点弯曲法[6-7]、振动波法和静态线形法[8]等索力测试方法虽有较好的理论依据，但在实际测量时由于各种因素的干扰，其效果不佳，亦很少采用。

斜拉索在索力和自重作用下会产生下垂，当不考虑拉索本身弯曲刚度时可认为索形呈悬链线[9-10]，如果斜拉索的垂度与索长之比(即垂跨比)很小则可认为索形呈抛物线[9]。

本文采用有限元方法通过分析斜拉桥拉索的索力和垂度之间的关系，提出一种通过测量拉索中间任意索段的垂度间接测量索力的新方法——垂度法。

1 斜拉索垂度影响因素

斜拉索的垂度不仅与拉索的索力、自重、索长、倾角以及大变形效应等因素有关[9]，而且拉索本身的弯曲刚度、边界条件(是否安装阻尼减振装置)等因素对拉索的垂度也会产生不同程度的影响。工程中常见的斜拉索有平行钢丝索和钢绞线索[2]，现以某斜拉桥平行钢丝索为例，选取6根不同长度、不同倾角的索，按索长从短到长依次编号为1#—6#，其参数见表1。采用有限元方法分析拉索的弯曲刚度和边界条件对其垂度的影响。

1.1 拉索弯曲刚度对垂度的影响

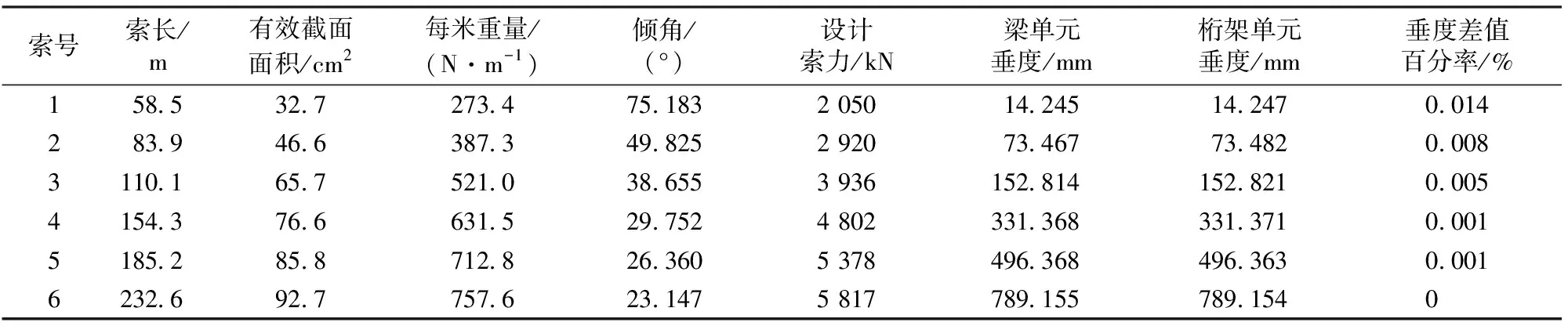
表1 拉索参数及弯曲刚度对拉索垂度的影响

对承受巨大拉力的斜拉索而言，其弯曲刚度应由2部分组成，一是本身的弯曲刚度，二是由于巨大拉力而产生的横向抗弯能力。用有限元方法分析拉索的垂度，考虑拉索的几何非线性和应力刚化效应，索单元可采用多直梁元法或多直连杆(桁架单元)法模拟[11]。为了分析拉索本身的弯曲刚度对拉索垂度的影响，采用ANSYS中的三维梁单元BEAM188和三维桁架单元LINK180分别建立斜拉索模型。梁单元可以同时考虑拉索本身抗弯刚度以及拉索绷紧后的应力刚化效应；桁架单元只有轴向刚度而没有抗弯刚度，也可以考虑应力刚化效应。通过比较2种单元模拟计算的斜拉索垂度，即可得出拉索本身弯曲刚度对拉索垂度的影响程度。

拉索本身的实际抗弯刚度应该介于索中高强钢丝之间完全粘接与完全不粘结时的弯曲刚度之间，且更接近于完全粘结时的弯曲刚度，比完全不粘结时的弯曲刚度大得多[12-13]。本文用梁单元计算时，将组成各拉索的高强钢丝都看成完全粘结计算其弯曲刚度，但将计算结果折减30%[12]。

为了正确计算垂度，2种模型中单元的长度均不大于拉索长度的1/100，且都考虑拉索的大变形效应和应力刚化效应。为了与桁架单元模型对比，梁单元模型中拉索两端的约束条件也假设为铰接。2种单元类型的索力均通过INISTATE命令实现，并通过迭代计算使拉索最下端的索力(拉索索力沿长变化，下端最小上端最大)等于表1中的设计索力。用2种单元计算的6根斜拉索的垂度见表1。

由表1的结果可知：索本身的弯曲刚度对垂度的影响很小，而且拉索越长其本身的弯曲刚度对垂度影响越小，尽管拉索越长其截面面积越大(本身弯曲刚度也越大)，说明拉索本身的弯曲刚度对垂度的影响几乎可忽略不计，即斜拉索可用桁架单元模拟，各个索段(单元)之间可以看成是铰接。

1.2 减振装置对拉索垂度的影响

斜拉索两端的边界条件应该介于完全刚结和铰接之间，较为接近刚结的情况[12]。拉索安装减振器后，会因其安装位置不同而对拉索的基频产生不同影响[3]，也会对拉索的垂度产生不同的影响。在拉索做微幅振动的情况下，减振器对拉索的作用可以视为拉索跨内的弹性支撑[10]。弹性支撑的刚度必然影响拉索的垂度，显然刚性支撑的影响最大。假设表1中的斜拉索在距离主梁锚固点3 m处设置减振器，将其视为垂直于斜拉索的刚性链杆支座，且拉索两端按刚接计算出的有无减振器时拉索垂度见表2。

表2 两端刚接时有无减振器条件下拉索垂度比较

由表2可以看出，减振器的设置对垂度的影响较大，但这种影响随着拉索的长度增加而减弱，即拉索越长安装减振器对垂度的影响也相对越小。

2 斜拉索不同位置索段的垂度

2.1 斜拉索中间索段的垂度

文献[8]指出，拉索只在端部一定范围内受到边界条件及弯曲刚度的影响，表现为梁行为，在中部的绝大部分范围内表现为索行为。根据这一结论和以上分析结果，可将离开端部一定距离后任意局部索段的两端近似为铰接进行其垂度计算。为验证这种处理方法的正确性，进行整根索模型和两端铰接索段模型下局部索段垂度的对比分析。

整根索模型下的索段垂度分析，选择表1中的1#索(短索)和6#索(长索)用梁单元建立全索模型，分别按拉索两端刚接无减振器和有减振器2种情况，计算其正中间索段AB的垂度。图1给出了正中间索段AB垂度的整根索计算模型。图中：T0为下端索力；TL为上端索力，f1为索段AB的垂度。先计算全索的变形，然后根据该变形后的索形计算AB段的垂度f1，结果见表3和表4。

图1 中间索段AB垂度的整根索计算模型

索号索长L/mAB弦长LAB/mLAB/L/%f1/mmf2/mm误差/%1#58.556.59713.28913.2870.01554.59312.36512.3640.00852.59011.47411.4720.01750.08510.40810.4080.00040.0686.6616.6600.01530.0513.7473.7460.0276#232.6230.699775.589775.6320.006228.698762.204762.2340.004226.697748.966748.9520.00250.02136.46636.4500.04440.01723.33823.3210.07330.01313.12813.1100.137

两端铰接索段模型下索段垂度分析，从拉索正中间截取AB索段，按两端铰接重新建立计算模型，如图2所示。图中：TA为下端索力，TB为上端索力，f2为索段垂度。在计算垂度时，取索段AB的平均索力与整索上对应AB索段的平均索力相同，无减振器和有减振器2种情况的计算结果分别见表3和表4。

图2 中间索段AB垂度的索段计算模型

索号索长L/mAB弦长LAB/mLAB/L/%f1/mmf2/mm误差/%1#58.553.59111.91811.9160.01751.58811.04311.0420.00950.08510.41010.4080.01940.0686.6626.6600.03030.0513.7473.7460.0276#232.6227.698755.701755.6360.009225.697742.400742.4120.002223.696729.327729.3050.00350.02136.46936.4500.05240.01723.34023.3210.08130.01313.12913.1100.145

从表3和表4可以看出：选取正中间一段拉索并按两端铰接重新建模计算出的垂度f2，与斜拉索两端刚接有减振器或无减震器时按整索分析得到的对应索段的垂度f1非常接近；当选取的索段其端点距离拉索锚固点或减振器支点较近时，f1和f2之间的误差偏大，当索段的端点离开拉索锚固点或减振器支点一定距离后，f1和f2之间的误差很小，拉索中间索段的垂度与拉索的边界条件几乎无关；选取的中间索段越短，f1和f2之间的误差越大。

2.2 斜拉索任意位置索段垂度

以表1中的6#长索为例，分析长度相同而在拉索中位置不同各索段的垂度。在如图3所示的6#索模型(无减振器)中选取A0B0，A1B1和AB弦长均为40 m的3段索进行分析，其中AB为正中间索段，计算结果见表5。

图3 拉索上的不同索段

索段名称倾角/(°)平均索力/kN垂度f1/mm直接误差/%修正后误差/%A0B022.5445 824.423.5470.8910.001A1B122.8475 837.223.4430.4460.003AB23.1475 850.323.339

在表5中，倾角为索段弦向与水平方向的夹角，直接误差=(任意索段垂度-AB索段垂度)/AB索段垂度×100%，修正后误差=(对任意索段垂度进行倾角和平均索力修正后的值-AB索段垂度)/AB索段垂度×100%。因为不同索段的平均索力和倾角不同，其垂度结果之间存在一定的差别。对任意索段的垂度进行倾角修正的方法是将原垂度除以该索段倾角的余弦值，再乘以AB索段倾角的余弦值；平均索力修正的方法是将原垂度除以AB段平均索力，再乘以该索段的平均索力。

从表5可以看出，长度相同的不同位置索段的垂度略有不同，其原因是他们所对应的倾角和平均索力略有不同，但是经过倾角和平均索力修正后的各索段垂度基本一致。这说明对某根拉索而言，长度相同、位置不同索段的垂度会因索段本身的倾角和平均索力不同而有所不同，但差别很小。

3 斜拉索中间索段索力与垂度的关系

3.1 中间任意索段垂度与索力的关系式推导

如前所述，斜拉索中间任意索段可以认为是两端铰接的。假设索段OME两端为铰接，其长度为L，倾角(即弦向与水平向的夹角)为α，单位长度拉索质量为m，单位长度索重为mg，索力在水平方向的分量为F，拉索最大垂度为fmax，如图4所示。

图4 斜拉索索段模型

取索段的一半OM为隔离体，如图4(b)所示，将拉索单位长度索重mg分解成垂直于弦线方向的mgcosα和平行于弦线方向的mgsinα2个分量，设TM为拉索中点处的索力即平均索力，对铰接点O取矩可得斜拉索平均索力TM与最大垂度fmax的近似关系式为

(1)

由于拉索自重的原因，拉索沿长度在不同位置的索力是不同的，上端索力大而下端索力小，每延米差值近似为mgsinα，由此可知斜拉索最下端的索力T0和最上端的索力TL分别为

T0=TM-0.5Lmgsinα

(2)

TL=TM+0.5Lmgsinα

(3)

若能测得斜拉索某索段的最大垂度fmax，则根据式(1)、式(2)和式(3)即可求得该索段的平均索力TM、最小索力T0和最大索力TL，进而求得该索段任意截面索力的大小。

3.2 有限元法计算的垂度-索力关系曲线与式(1)计算结果比对

对于索力与垂度的函数关系，除了用解析方法进行理论推导外，还可以按有限元法计算得到索力—垂度关系曲线。利用有限元法不仅可以考虑拉索本身的弯曲刚度、边界条件(包括阻尼减振装置)等因素的影响，还可考虑拉索的大变形效应和应力刚化效应，计算结果与工程实际非常接近，并且可以实现参数化编程计算。输入拉索弦长(图4中对应的弦长L)、倾角α、有效截面面积(钢丝或钢绞线截面有效面积之和)、单位长度质量m后，假设索的设计索力为T0(拉索下端的最小索力T0)，让索力在某个区间变化(如0.2T0～2.0T0)，第1次计算索力为0.2T0时对应最大垂度，然后每次增加0.05T0，直至索力为2.0T0。这样，对每根拉索都可得到1条索力—垂度关系曲线。按式(1)计算同样可以得到索力—垂度关系曲线。图5为表1中6#斜拉索分别用有限元法和按式(1)计算的索力—垂度关系曲线。

图5 不同计算方法得到的索力—垂度关系曲线

由图5可以看出，尽管式(1)做了一些近似假设，对6#拉索而言，在索力较大时其计算结果与有限元法的结果非常接近，仅当索力较小时才能看出二者的差别。而实际工程中的斜拉索索力都较大，因此，式(1)的计算精度完全可以满足实际工程需要。与有限元法相比，式(1)计算简单、方便，便于在实际工程中推广应用。

3.3 环境温变化对垂度与索力关系的影响

斜拉桥索力现场实测数据表明，索力受环境温度变化的影响较为敏感[14]，主要体现在两个方面：一是由于梁、塔因温度变化产生的变形(拉索上、下锚固点距离变化)，引起锚固于梁、塔上的斜拉索索力发生变化；二是温度变化引起拉索的伸长与缩短(假设拉索上、下锚固点距离不变)，从而引起索力变化。前者相当于对拉索进行张拉或放张，因而不会影响索力与垂度之间的函数关系，所以可仅研究后者对斜拉索的影响。以垂度较大的6#索(初始索力5 817 kN，材料线膨胀系数1.2×10-5/℃)为例，计算其在两端点位置不变的情况下，升温与降温对索力及垂度关系的影响，结果见表6。其中，垂度1为将初始索力施加在6#索计算模型上，然后再施加变温荷载用有限元法计算的垂度结果；垂度2为根据变温后索力用式(1)计算的垂度值；垂度误差=(垂度2-垂度1)/垂度2×100%。

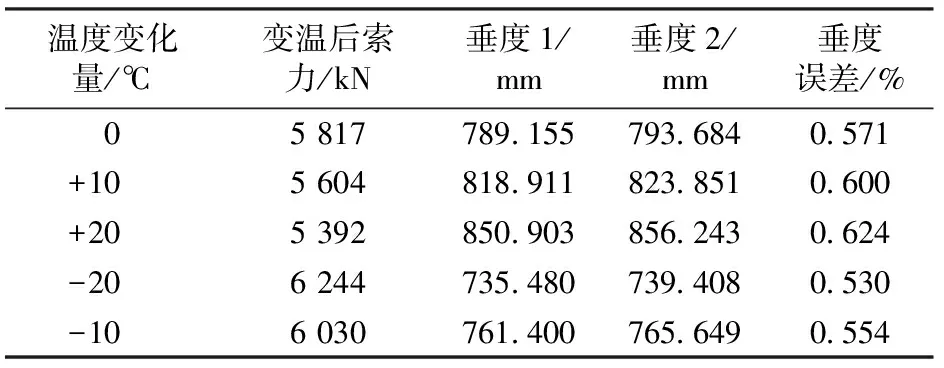
表6 温度变化对6#索垂度及索力的影响

表6可以看出：温度变化后拉索索力和垂度都发生明显变化，但两种算法得到的垂度误差较小，这说明变温后索力与垂度之间的函数关系依然基本保持不变，即温度变化不影响索力与垂度之间的函数关系，式(1)是适用的。

4 垂度法测索力的原理和步骤

4.1 垂度法测索力的原理

由上述分析可知，在对整根斜拉索分析中，离开其两端位置一定距离，选取适当长度的任意索段AB的垂度与对应的索段分析(两端铰接并忽略拉索本身弯曲刚度的影响)的结果几乎相同。可认为，索段AB甚至整个斜拉索的索力，可通过测量该索段的垂度，应用式(1)、式(2)和式(3)求得。这种测量索力的方法称为垂度法。

4.2 垂度法测索力的步骤

垂度法测索力的一般步骤如下：

(1)在斜拉索适当(离开拉索端部一定距离)位置上任取适当长度的索段(选取的索段越长越精确)，用仪器测量出该索段的倾角、弦长和最大垂度；

(2)按式(1)计算所选索段的平均索力；

(3)根据索段的平均索力、每延长米的索力差mgsinα和索段的位置确定整个拉索最小索力T0和整个斜拉索的平均索力TM。

5 试验验证

5.1 斜拉索试验模型设计

斜拉索模型试验的目的是验证垂度法测量拉索索力的有效性和可行性。按图6所示的加载方法进行加载试验，模型索下端锚固于地锚上，上端绕过定滑轮并吊一重物作为模型索的张拉力。定滑轮与模型索之间的摩阻属于滚动摩擦，经试验测定其摩阻力不超过吊重的1%，试验中忽略定滑轮与模型索之间的摩阻力，则重物的重量即为拉索上端的张拉力，亦即索力的真值。

图6 模型加载示意图

采用型号为“6×19+IWS”的钢丝绳作为模型索模拟表1中6#斜拉索。根据相似理论，模型必须满足在几何尺寸、弹性模量、荷载等方面的相似性[15]。首先在试验室测定所选定钢丝绳的截面面积和弹性模量，然后再根据相似关系确定模型的其他参数。原型索与钢丝绳模型的参数见表7，其中原型索的参数数据均取自实桥的设计图，模型索采用的是细钢丝绳，其弹模由拉伸实验测出。根据相似理论，配重的计算式为

(4)

式中：G配重为每延米应配重量；q原型为原型索每延米重量；λ为几何缩尺比；E模型为模型索弹模；E原型为原型索弹模；q本身为模型索本身每延米重量。

表7 模型索与原型索参数对比

试验时，配重采用在钢丝绳上布置一定间距的小U型螺栓的方法实现，即通过调整小U型螺栓的间距满足模型索所需的每延米重量。

试验前先对吊重称重。试验时，先在模型索上标记A，M和B点(如图6所示)，其中M点为索段AB的中点；然后用全站仪测量拉索上A，M和B三截面中心点的三维坐标，进而计算出AB索段的垂度f、弦长L和倾角α；最后用式(1)计算索段的平均索力TM，用式(3)计算模型索上端的索力TL并与索力真值(即吊重重量)进行比较。图7为斜拉索模型试验现场。

5.2 试验结果

模型试验时通过改变模型索的倾角、索段长度以及吊重进行多次测量。表8列出了其中3次试验结果。

图7 模型试验现场

编号每米重量m/(N·m-1)弦长L/mm垂度f/(mm)倾角α/(°)实测索力TL/kN索力真值(吊重)/kN索力误差/%128.3116 86267.723.46313.45413.2761.341228.3116 07651.324.59815.97815.7061.732328.3113 31936.130.02314.84815.706-1.512

表8中索力误差为：(索力真值-实测索力)/索力真值×100%。试验结果表明：3次试验测得的索力与索力真值(实际吊重)比较其误差均在2%以下。这说明垂度法测索力不仅可行，而且测试结果准确可靠，关键是要准确测出所选索段AB的垂度f、弦长L和倾角α。

6 结 论

(1)对斜拉索而言，离开其锚固位置和阻尼减振装置一定距离后，选取其中部任意(适当长度)索段分析索力与垂度关系时，索段两端可看成是铰接，拉索本身的弯曲刚度可以忽略不计，并且索力与垂度之间存在确定的函数关系。

(2)当索力较大而垂度较小时，按抛物线索型推导的索力与垂度之间关系比较简洁且精度较高，与考虑拉索诸多影响因素的有限元法结果非常接近，并且这种关系几乎不受两端的支承条件和环境温度等索段外其他因素及斜拉索本身的弯曲刚度的影响。

(3)拉索模型试验结果表明，依据斜拉索中间索段的索力与垂度关系建立的索力测试方法(垂度法)可行，并且测试结果准确可靠。