机械因素对齿轮传动轴系扭转振动的影响分析
2013-09-16陈勇
陈 勇
(西南电子技术研究所, 四川 成都 610036)
机械因素对齿轮传动轴系扭转振动的影响分析
陈 勇
(西南电子技术研究所, 四川 成都 610036)
齿轮传动系统是雷达伺服传动系统的常用形式,其扭转振动对雷达伺服机构的响应速度和稳定性有重要影响。以某雷达第一级齿轮传动系统为研究对象,基于工程软件ANSYS/LS-DYNA,应用显示中心差分法分析了支撑位置、轴径尺寸、轴上质量分布等机械参数对齿轮传动系统扭振响应的影响,通过对比分析,得出这些机械因素对齿轮传动系统扭振响应特性影响的定性结论,为进一步分析雷达伺服系统提供指导。
齿轮传动;扭振;中心差分法;机械因素;LS-DYNA
引 言
伺服传动机构是雷达系统的重要组成部分,齿轮传动是伺服传动系统中最常用的形式。齿轮传动系统作为复杂的多体非线性动力学系统,扭转振动是其主要振动形式[1],也是影响雷达伺服机构响应速度和稳定性的重要因素。而特定的齿轮传动系统都有一个固有扭振频率,它与齿轮传动系统的转动惯量、刚度、阻尼等机械参数有密切的关系。随着雷达系统对目标跟踪速度、定位精度的要求越来越高,对伺服传动系统的精度、响应速度和稳定性的要求也越来越高。因而,机械参数对齿轮传动系统扭转振动的影响研究对提高雷达伺服传动系统的性能具有重要的意义。
目前轴系扭振的计算方法主要包括Holzer法、传递矩阵法和有限元法[2]。本文以LS-DYNA为计算平台,应用显示中心差分法分析了转动惯量、支撑位置、质量分布等对齿轮传动系统固有扭振频率和幅值的影响。
1 齿轮传动系统的动力学分析
1.1 扭转振动计算方法
在国内外对传动系统扭振的分析过程中,传统的理论计算分析将传动系统简化为多自由度的惯性-弹簧系统,通过测试系统各零部件的惯性参数和刚度参数,计算扭振的固有特性。其中轴系扭振的建模方法发展出了分布质量模型和集中质量模型,计算方法发展出了Holzer法、传递矩阵法和系统矩阵法等多种分析方法[1-3]。这些方法对齿轮传动进行简化处理,并不能很好地反映扭振过程中齿轮啮合传动的影响。
1.2 中心差分法
在动力学有限元分析中,系统的控制方程可描述为[4-6]
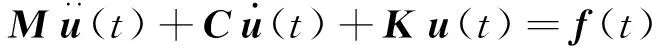
(1)

(2)
(3)
将式(2)、(3)代入式(1)可得求解各离散时间点的递推公式:
(4)
可用式(4)求解各离散时间点的位移值,但由于中心差分法是条件稳定算法,即用它求解具体问题时,时间步长Δt必须小于该问题求解方程性质所决定的某个临界值Δtcr,否则算法将不稳定。算法的稳定性条件:

(5)
式中:Tn为有限元系统的最小固有振动周期。在实际应用中,Δtcr可由下式进行估计:

(6)
式中:lmin为最小单元长度;ρ为材料密度;υ为材料泊松比;E为材料弹性模量。
在轴系的扭振计算中,必然涉及到齿轮的时变啮合刚度、齿侧间隙、轴承滚珠与内外圈的接触刚度等强非线性特性。如果采用经典的扭振理论计算公式或隐式计算方法来求解轴系的扭振问题,将对轴系模型进行大量简化,会忽略许多与扭振频率相关的因素,必然导致求解精度下降。本文采用显示中心差分法,主要是考虑到该方法在求解非线性问题上的优势。因为在非线性分析中,每一个增量步的刚度矩阵都会被修改,这时采用显示算法,避免了矩阵求逆运算,计算上的好处更加明显。另外,采用中心差分法可以通过控制其时间步长来达到计算时间与计算精度的平衡,以最少的计算时间来满足求解精度的需要。
2 弯振的消除
在通常情况下,轴系旋转时,扭振与弯振同时存在。设轴旋转角速度为ω(规定逆时针方向为正方向),扭振角速度为ωr,弯振速度为V,其速度分量为Vy,该分量将产生附加角位移:

(7)
式中:R为转子半径。对于高精度扭振分析来说,必须消除弯振对扭振分析的影响。
在笛卡尔坐标系下获得的位移信息中,只要选取同一轴截面直径上两端的节点,排除其平动特性,即可消除弯振信息。图1所示为消除弯振影响原理图,在轴截面上取直径上的两个点,确定这两个点X方向和Y方向的相对距离uX、uY,基本上可以消除弯振的影响。

图1 消除弯振影响的原理图
由于LS-DYNA中的瞬态动力学输出结果是在笛卡尔坐标系下的节点位移结果,不能直接反映出结构的扭振特性。因此,需要把笛卡尔坐标系下的位移结果转换为柱坐标系下的时间与扭转角之间的关系曲线,才能获得伺服转台齿轮传动系统的扭振特性。
3 机械参数影响分析
影响伺服转台齿轮传动系统扭振响应的主要因素有干扰力矩和轴系的动态特性。两者的共同作用决定了轴系扭振响应的特性。
对于伺服转台齿轮传动系统,轴系的动态特性主要针对特定的干扰力矩而言,轴系在整个工作转速内的扭振响应越小越好。影响伺服转台齿轮传动系统扭振响应的主要因素在于轴系动态特性3个方面的性质:1)工作转速内的共振频率,它是系统产生共振的关键;2)系统的振型,即幅值和相位的关系,它决定了系统扭振响应的强弱;3)阻尼对扭振的抑制作用,适当的阻尼可以消耗干扰力矩的输入能量,削弱共振响应的峰值。
下文以一级齿轮传动为例,分析支撑位置、质量分布、轴径尺寸、轴的材料密度等机械参数对齿轮传动系统扭振特性的影响。
3.1 一级齿轮传动系统的仿真分析模型
图2所示为某雷达伺服转台第一级直齿齿轮传动模型。该级齿轮传动由额定转速为955 rpm的伺服电机驱动。齿轮模数为0.8,齿数分别为26和67。齿轮及轴的材料为40Cr,弹性模量为211GPa,泊松比为0.28。由于LS-DYNA分析中施加转速为固定边界条件,不是初始条件,因此,在施加转速时应由零逐渐增加至额定转速值,这样能够避免因突然施加转速而造成系统分析结果不稳定的问题。现以斜坡曲线加速到额定转速955 rpm,施加的速度曲线如图3所示。对齿轮与齿轮、轴承与轴系之间的接触算法采用自动面对面滑移接触算法,采用了质量缩放因子以兼顾时间与精度的平衡。

图2 齿轮传动系统原始结构有限元模型

图3 电机转速施加曲线
由LS-DYNA瞬态动力学分析软件计算俯仰传动系统在955 rpm转速下、0.4 s内的瞬态动力学特性,根据计算结果,经过坐标转换得到该模型的扭振时域曲线,如图4所示。
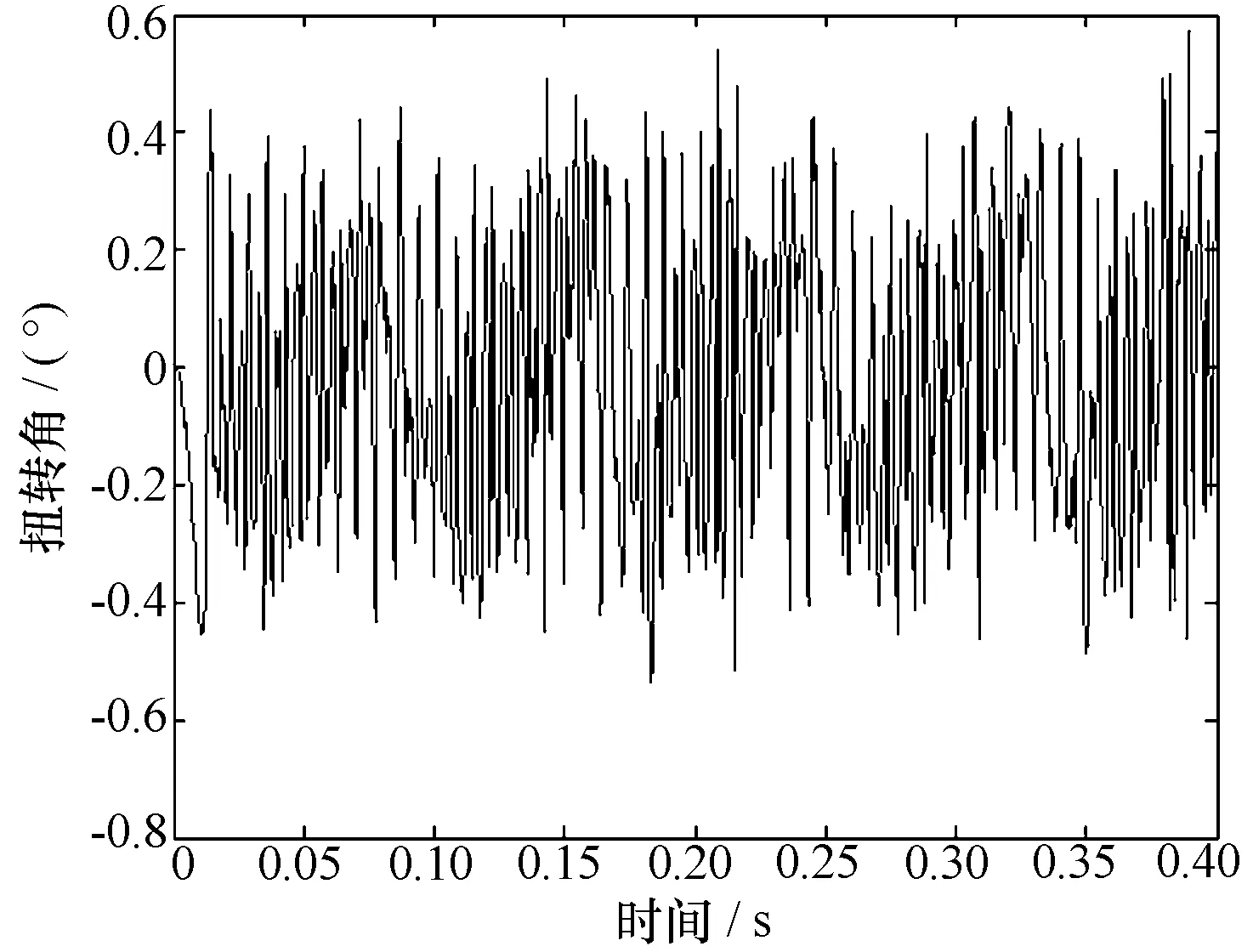
图4 原始结构的扭振时域曲线
再通过FFT(快速傅里叶变换)得到该模型的扭振频域曲线,如图5所示。
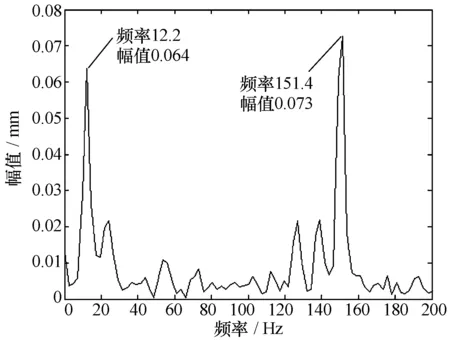
图5 原始结构的扭振频域曲线
3.2 改变支撑位置的仿真
仅将大齿轮轴的支撑位置向内平移7 mm,得到的有限元模型如图6所示。

图6 改变支撑位置的有限元模型
在其他条件与3.1节相同的情况下应用LS-DYNA计算0.4 s内的瞬态动力学特性,根据计算结果,经过坐标转换得到该模型的扭振时域曲线,如图7所示。

图7 改变支撑位置的扭振时域曲线
再通过FFT得到该条件下的扭振频域曲线,如图8所示。

图8 改变支撑位置的扭振频域曲线
对比图8和图5可知,支撑位置的改变不能改变系统的扭振频率,但可以影响扭振的幅值。
3.3 改变轴上质量分布的仿真
在大齿轮轴齿轮外侧增加一圆盘质量块,得到的有限元模型如图9所示。
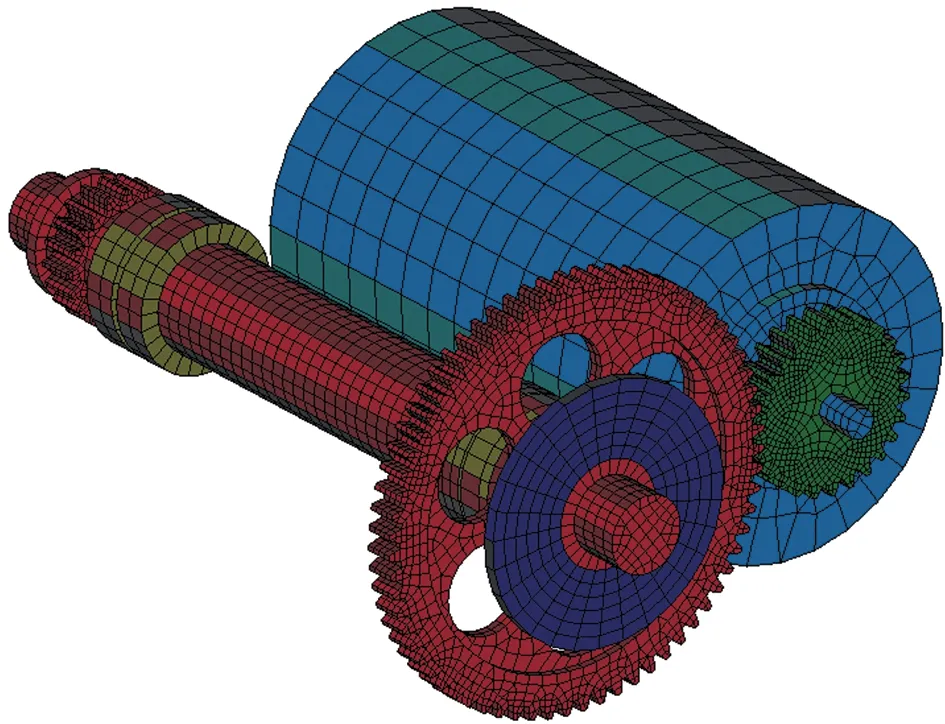
图9 改变轴上质量分布的有限元模型
在其他条件与3.1节相同的情况下应用LS-DYNA计算0.4 s内的瞬态动力学特性,根据计算结果,经过坐标转换得到该模型的扭振时域曲线,如图10所示。

图10 改变轴上质量分布的扭振时域曲线
再通过FFT得到该模型的扭振频域曲线,如图11所示。

图11 改变轴上质量分布的扭振频域曲线
对比图11和图5可知,在啮合区域以外的部位,改变轴上质量分布不能改变系统的扭振频率,对扭振幅值略有影响。
3.4 增大轴径的仿真
大齿轮轴直径增大10 mm,得到的模型如图12所示。

图12 增大轴径的有限元模型
在其他条件与3.1节相同的情况下应用LS-DYNA计算0.4 s内的瞬态动力学特性,根据计算结果,经过坐标转换得到该模型的扭振时域曲线,如图13所示。
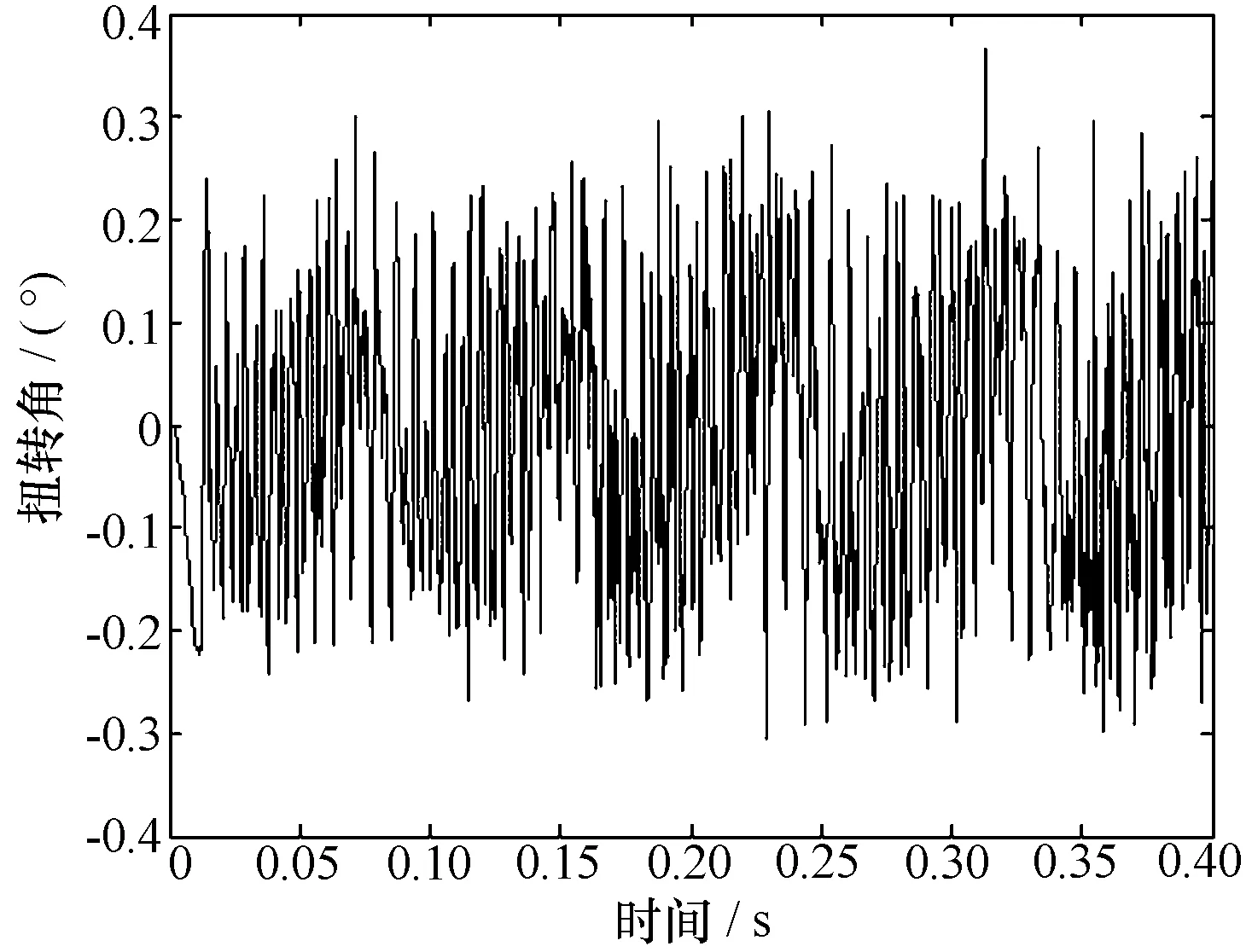
图13 增大轴径的扭振时域曲线
再通过FFT得到该结构第一根轴的扭振频域曲线,如图14所示。

图14 增大轴径的扭振频域曲线
对比图14和图5可知,增大轴径不能改变系统的扭振频率,但可以较大地降低扭振的幅值。
4 结束语
本文以某雷达伺服传动系统的第一级齿轮传动为例,通过改变支撑位置、轴上质量分布以及轴径等机械因素,分析了这些因素对齿轮传动系统扭振响应特性的影响,可以得出如下结论:
1)齿轮传动系统的扭振频率对支撑位置、轴上质量分布和轴径的变化等结构因素不敏感。
2)改变支撑位置和增大轴径能有效降低扭振幅值,控制扭振响应。
通过定性分析支撑位置、轴径尺寸、轴上质量分布等机械因素对齿轮传动系统扭振响应特性的影响,可以为改善雷达伺服传动系统扭振响应提供有益参考。
[1] 周林, 郑四发, 连小珉. 加速工况下传动系统扭转振动分析[J]. 振动工程学报, 2010, 23(6): 601-605.
[2] 潜波, 巫世晶, 路红山. 基于传递矩阵法的车辆传动系统扭转振动分析[J]. 武汉大学学报:理学版, 2005(S2):203-207.
[3] 周杰梁, 郑百林. 基于中心差分法的纤维结构碰撞动力学分析[J]. 力学季刊, 2011, 32(3): 466-472.
[4] 谢诞梅, 刘占辉, 杨长柱, 等. 汽轮发电机组轴系扭转振动对机械参数的敏感性分析[J]. 动力工程, 2005, 25(4): 462-465, 482.
[5] 林利红, 陈小安, 缪莹赟. 接触非线性结构的随机振动数值仿真分析[J]. 中国机械工程, 2009, 20(11): 1352-1355, 1360.
[6] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005.
[7] BELYTSCHKO T, LIU W K, MORAN B. 连续体和结构的非线性有限元[M]. 庄茁, 译. 北京: 清华大学出版社, 2002: 269-275.
[8] CROWTHER A R, ZHANG N. Torsional finite elements and nonlinear numerical modeling in vehicle power-train dynamics[J]. Journal of Sound and Vibration, 2005(284): 825-849.
[9] ZHANG Z C, ZHAO Y, LIN J H. Non-stationary random vibration analysis for vehicle-bridge coupled systems[J]. Journal of Vibration Engineering, 2007, 20(5): 439-446.
陈 勇(1977-),男,硕士研究生,工程师,主要从事雷达结构设计工作。
Analysis on the Effects of Mechanical Factors on Torsional VibrationBehavior of Gear Transmission
CHEN Yong
(Southwest China Institute of Electronic Technology, Chengdu 610036, China)
Gear transmission is a common method for radar servo driving system, its torsional vibration can directly influence the response speed and the stability of radar servo system. Aiming at the first level gear transmission system of a radar, based on the software of ANSYS/LS-DYNA, the effects of some mechanical factors such as supporting position, shaft diameter and mass distribution of shaft on the torsional vibration response are studied by the center difference method. Some qualitative conclusions are presented by comparison analysis. The research results will guide further study of radar servo system.
gear transmission; torsional vibration; center difference method; mechanical factors; LS-DYNA
2013-07-22
军工制造业数字化技术重大项目(A1120131044)
TH132.41;TH113.1
A
1008-5300(2013)06-0036-04
