机载雷达天线座的三坐标测量方法及误差分析

张立琴

(南京电子技术研究所， 江苏 南京 210039)

机载雷达天线座的三坐标测量方法及误差分析

张立琴

(南京电子技术研究所， 江苏 南京 210039)

三坐标测量机是目前使用较广泛的一种高精度测量仪器，被广泛应用在各个生产领域。在实际的测量过程中，由于选择基准和测量方法的不同，测量所产生的误差也不同。基于三坐标测量概念，对机载雷达天线座零件的实际测量中影响测量精度的因素进行分析，并针对性地提出一些测量方法。

同轴度；三坐标测量；截面圆；误差

引 言

三坐标测量机的使用越来越广泛，它具有测量精度高、范围广，方便、快捷的优点，特别是在零件的形位误差和一些不易实现准确测量元素的检测中。目前三坐标可以使用的测量方法很多，据相关的数据统计，单使用三坐标测量机测量零件的形位误差，测量方法就超过了一百种。对于测量方法的选择，通常都是根据被测机械零件和测量仪器来确定，如果测量方法不正确，就会影响测量误差，难以保证测量结果的准确性，严重影响了对机械零件质量的判断。机载雷达天线座中的基座、万向支架是天线座的核心零件，其制造精度特别是同轴度的误差直接影响整个天线座的方位及俯仰精度。在长时间的测量工作中，我们总结出一些减小、避免误差的同轴度测量方法。

同轴度的检测是我们在机械加工测量中经常遇到的问题，通常检测零件的同轴度是比较困难的，零件的精度往往只能靠设备和加工者的经验来保障。利用三坐标测量机进行同轴度检测，既直观又方便，测量精度高，免去了常规方法检测用的检具(如心棒)的设计与制造所需的时间和费用，大幅度降低了生产成本，缩短了生产周期。但在实际测量工作中，由于测量方法不当，可能会出现测量结果误差大等问题。特别是测量机载产品的天线座、万向支架等，这类产品均有着精度要求高、基准很短而被测元素很长或者基准与被测元素相距很远的特征。对此，我们进行了分析研究，并提出了相应的检测方法。

1 同轴度误差的产生因素

根据GB/T 1182—2008中同轴度误差的定义：同轴度是指被测圆柱面轴线对基准轴线不共轴的程度。轴线的同轴度公差的定义为“公差带是半径差等于公差值t(图为直径公差值Φi)的两同轴圆柱面所限定的区域”[1]，如图1所示。

图1 同轴度定义图

从测量原理上说，三坐标测量机直接测得的是被测工件上一些特征点的坐标位置，需要通过软件运算构造出测量元素，进而进行同轴度的计算。因此被测工件的同轴度误差主要与下列因素有关：

1)基准元素与被测元素的形状误差。主要包括孔(或轴)的圆度误差、直线度误差、投影面和基准轴线的垂直度误差等。这些误差对测量的结果影响极大。一般来说，很难对工件进行全面的测量，在采样点较少的情况下，即使测量机没有误差，不同的采样点也会导致截然不同的测量结果。

2)算法计算误差。因为被测几何元素不是理想元素，在数据处理过程中总是用一近似的理想元素替代它，这一过程叫做拟合算法计算。常用的算法有：最小二乘法和最大最小条件法[2]。从理论上讲计算机获得的采样点越多，拟合的精度就越高。

3)基准轴线与被测轴线的长度及相互间距离引起的误差放大。被测元素如果离基准元素较远，则误差会被成倍放大。

1.1 基准元素与被测元素的形状误差引起的测量误差

1.1.1 圆度误差带来的测量误差

三坐标测量机最初获得的只是特征点的坐标，换言之，三坐标测量机是通过有限的特征点来构造一个截面圆。考虑一个圆度不好的截面圆，其特征点坐标的理论值与实际值存在较大误差，那么该截面圆圆心坐标的理论值与实际值将产生较大的偏差。这将直接导致基准轴线或被测轴线的直线度误差变大，从而产生轴线偏离，以此来测量同轴度将会产生较大的偏差。

1.1.2 投影面和基准轴线的垂直度问题

这是测量过程中极其重要的一步。众所周知，一个三维空间中的圆在与它的法线矢量垂直的平面上的投影是圆，而在平面上的投影是椭圆或线段。尽管理想条件下椭圆和圆的质心是重合的，但工件并不是理想的，当圆度误差较大时，由于投影面与基准轴线不垂直，两者质心的空间坐标便存在着较大的差异。这就带来了由投影面与基准轴线的垂直度误差所引起的测量误差。

1.1.3 直线度误差对测量结果的影响

有些产品在测量过程中发现其基准轴线有轻微扭曲的现象，这便导致拟合得出的轴线与零件实际轴线存在一个夹角。于是测量结果自然不能符合图纸要求。

严格地说，上述测量误差并不是由三坐标测量机引起的，而是零件本身的问题导致测量结果不确定。

1.2 算法计算误差引起的测量误差

三坐标测量机构造测量元素所依赖的最小二乘法是以概率统计为基础的，但不符合国际上的规定，即不符合最小条件的评定原则。所以要求采样的特征点数达到一定的数量。当采样点过少时，构造所得的测量元素随机性较大，从而导致测量结果的不确定度变大。当采样点过多时，会较大程度地引入三坐标测量机的系统误差，同时使得测量过程冗长繁琐。

1.3 基准轴线与被测轴线的长度及相互间距离引起的误差放大

这是在三坐标测量中最具争议的一项误差，在日常测量中常常遇到。例如，测量某机载产品万向支架(图2)中E、F两圆柱的同轴度(图纸要求为Φ0.02 mm)，其中E为基准圆柱，F为被测圆柱，两圆柱轴长均为10 mm，两轴端距离为160 mm。通常的测量方法是在基准圆柱上测量两个截面圆，构成一基准轴线。同时在被测圆柱上也测量两个截面圆，然后计算同轴度。由于基准上两个测量截面的距离很小(10 mm)，基准第一截面与被测第一截面之间的距离很大(160 mm)，根据三角形相似原理(见图3)，原先在基准轴线上的较小误差(5 μm)被放大成了一个很大的误差(80 μm)。这一测量结果大大超出了图纸加工要求，不能真实反映零件的情况，且由于测量截面距离较短，测量重复性差，检测数据不可靠，若以此为结论必将造成对零件的误判。

图2 万向支架示意图

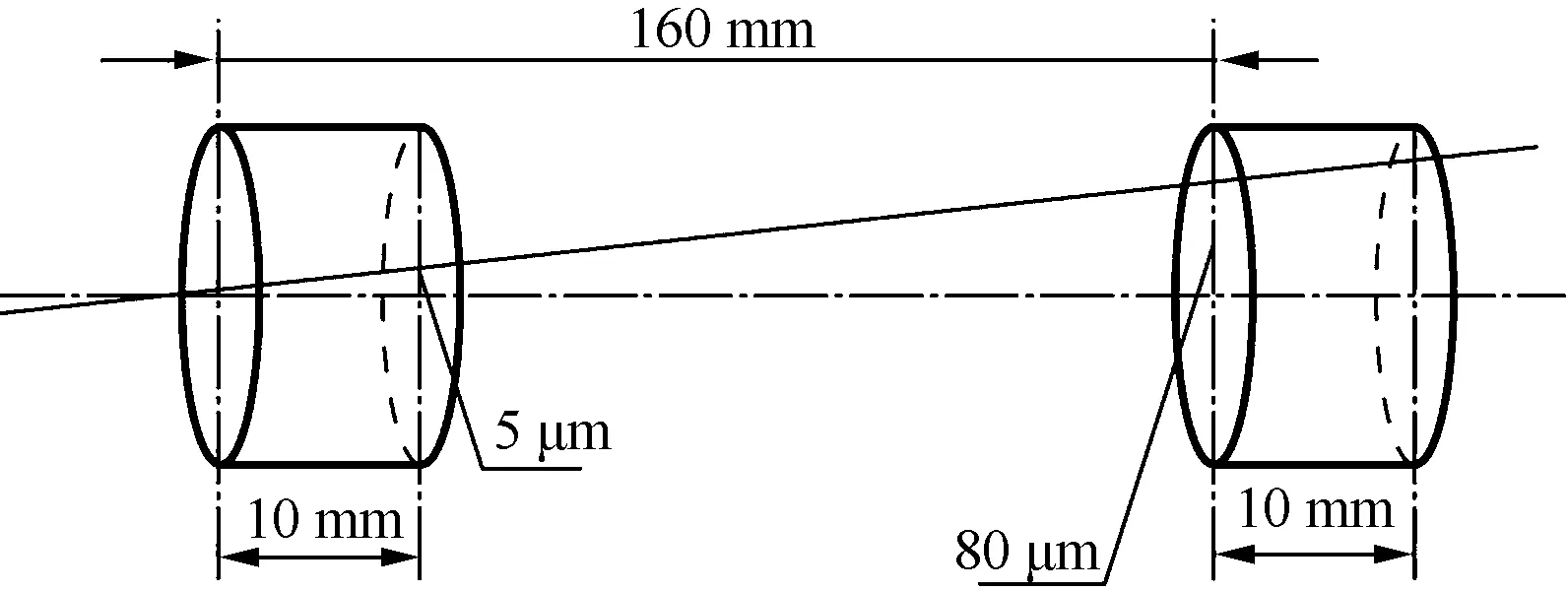
图3 误差放大效果图

2 解决办法

为解决上述难题，经过多次试验和论证，得出了以下经验，供大家参考。

1)针对投影面和基准轴线的垂直度问题给测量带来的影响，首先要求加工者加工时保证这一垂直度和投影面的平面度。如果实在无法避免这一问题，可以采用手动采点测量一个圆柱，手动建立工件坐标系之后再用自动测量精建坐标系。这样就可以使截面圆得到正确的投影。

2)尽量不要在太靠近孔口(轴端)的地方采点构造截面圆，同时增加每一个截面的点数。采点数控制在10～16个，以保证一定的采样量。尽量使用自动测量执行这一测量过程，并尽可能采集整圆。增加截面数和点数将无限逼近被测元素的实际形状，这无疑减小了测量的误差。

3)针对基准轴线与被测轴线的长度及相互间距离引起的误差放大问题，在测量中可采取以下处理方法：

a)建公共轴线法[3]。当基准圆柱与被测圆柱较短且距离较远(如图2所示的万向支架)时，我们选择在基准圆柱E和被测圆柱F上测中间截面，截面连线作为基准轴线，然后分别计算基准圆柱E和被测圆柱F对基准轴线的同轴度，取其最大值作为该零件的同轴度误差。通过这种方法测量F圆柱对E圆柱的同轴度为0.012 mm，满足图纸要求。有时我们也可以将加工工序中未改变装夹而一气呵成的孔或轴(非基准)连带基准轴线一起建立新的基准轴线，目的在于拉近基准轴线和被测轴线的距离。这种方法在工作中应用颇为广泛，取得了较好的效果。

b)考虑实际工作或装配要求作变通处理。为了使三坐标测量机测得的数据符合原设计要求，设想利用孔的端面作为基准(假设端面与孔的轴线有垂直度的要求)，将两端短圆柱分成若干个截面圆进行测量，然后将截面圆投影到端面上，即可得到所有截面圆的圆心的坐标，通过计算找出最大的圆心距γ，则根据同轴度的定义，两端孔的同轴度为2γ。利用孔的端面作为基准来检测同轴度误差的方法均能达到满意的测量效果。

c)改测同轴度为测直线度[3]。同轴度为被测元素和基准元素轴线间最大距离的两倍。在被测元素和基准元素上多采截面，然后用圆心构造出一条直线，用直线度近似代替同轴度(直线度×2)。因为这种情况下轴的倾斜对装配影响较小，而轴心偏移对装配影响较大，这种方法工作截面越短效果越好。

3 结束语

上述方法在实际测量过程中得到了广泛的应用，实践证明切实可行。三坐标测量机测空间点坐标精度很高，但并不等于对具体对象所得结论的精度很高。这是因为从点坐标到具体对象所需的结论参数有一个基于空间解析几何的计算过程。通过对同轴度误差产生因素的分析和对三坐标测量机测量特性的研究，很好地解决了这些采用一般数学方法处理误差较大的问题。

[1] 中国国家标准化管理委员会. GB/T 1182—2008 产品几何技术规范(GPS)几何公差现状、方向、位置和跳动公差标注[S]. 北京：中国标准出版社,2008.

[2] 熊有伦. 精密测量的数学方法[M]. 北京: 中国计量出版社, 1989.

[3] 刘新宇,郭会,张增良. 三坐标测量机同轴度误差分析[J]. 华北航天工业学院学报, 2003(2)： 6-7.

[4] 费业泰. 误差理论与数据处理[M]. 北京：机械工业出版社, 1994.

张立琴(1963-)，女，工程师，主要从事精密测量及质量控制工作。

Method and Error Analysis of Coordinate Measuring for Airborne RadarAntenna Pedestal

ZHANG Li-qin

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

Coordinate measuring machine is one kind of high precision measuring instruments. It is recently widely used and applied in different production fields. In actual measurement, the measurement error varies with the difference of selected criteria and measuring methods. Based on the coordinate measuring concept, the factors affecting the accuracy in practical measurement of the parts of airborne radar antenna pedestal are analyzed, and some measuring methods are proposed accordingly.

concentricity; coordinate measuring; circular cross-section; error

2013-11-13

TH7

A

1008-5300(2013)06-0051-03