适用空间网格结构模态识别的改进功率谱峰值法

张毅刚，刘才玮，吴金志，彭天明

(1.北京工业大学 空间结构研究中心，北京 100124;2.北京工业大学 城市与工程安全减灾省部共建教育部重点实验室，北京 100124;3.北京数泰科技有限公司，北京 100080)

利用实时监测数据进行结构异常及损伤诊断是健康监测的基本目的。自然环境激励下，模态参数识别为仅基于输出响应的系统识别［1］。目前已有多种方法:如功率谱峰值法(PP)、自然激励技术(NEXT)、频域分解法(FDD)、随机子空间法(SSI)等。由于峰值法具有识别模态参数速度快，直观性强，易操作特点，在建筑工程中应用较多。但实际应用中须采取适当方法进行信号处理，否则会极大影响识别精度，出现模态遗失现象。谢献忠等［2］利用该方法对湘潭某钢管混凝土拱桥的动力特性进行分析，结果表明识别效果较好;姜浩等［3］系统研究了基于环境激励下频域方法功率谱峰值法的基本理论，给出利用功率谱峰值法识别结构模态参数的操作流程。但其前提为所求频率必须稀疏。王锦文等［4］利用功率谱峰值法对深圳市民中心网架结构进行模态识别及模型修正;郑毅敏等［5］利用功率谱峰值法对杭州市民中心高空钢结构连廊进行模态参数识别及有限元模型修正。

综上所述可得出功率谱峰值法存在的问题有:①功率谱峰值法较适用于频率稀疏结构，而空间网格结构具有自振频率密集、空间耦合振动明显特点及自然环境振动下结构动力响应测试数据幅值小、随机性强，因此用功率谱峰值法对空间网格结构模态参数识别时会遇到遗漏模态及重叠频率无法筛选问题;② 传统方法在频率识别时单纯采用取极大值的数学方法，峰值选取过于主观，未与结构的理论模型相联系。

针对上述问题，本文在传统功率谱峰值法基础上进行改进，据空间网格结构模态密集特点提出若干判断准则，以结构理论振型为基础的辅助正则化功率谱算法，使其适用于空间网格结构。同时据此改进算法编制功率谱分析软件，并应用于深圳大运会主场馆钢屋盖的振动监测中。

1 功率谱峰值法

1.1 基本方法

据多自由度系统动力分析理论，动态方程可用正则坐标表示为:

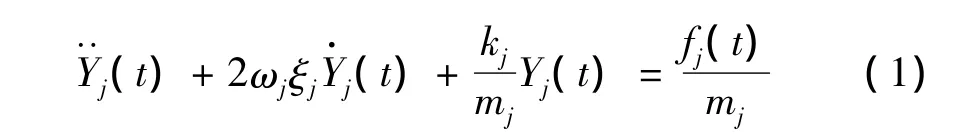
式中:ωj，ζj，kj，mj，fj(t)分别为第 j振型的频率、正则化刚度、阻尼比、质量及外力。经推导［6］第p点真实响应信号自谱Gvp(ω)为:

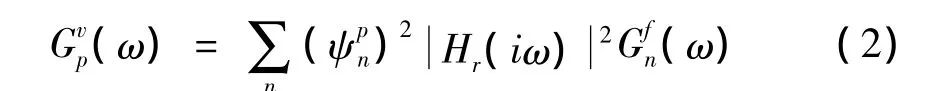
式(3)可用幅值及相位形式表示，其中相位角为:

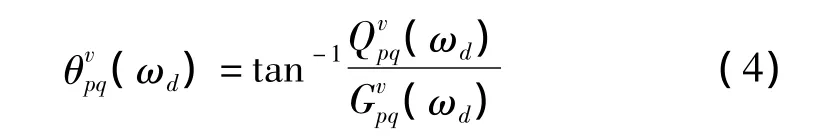
在测点较多情况下，可利用平均正则化功率谱选取峰值以含所有测点的功率谱密度信息，进行频率识别。计算公式为［3］:

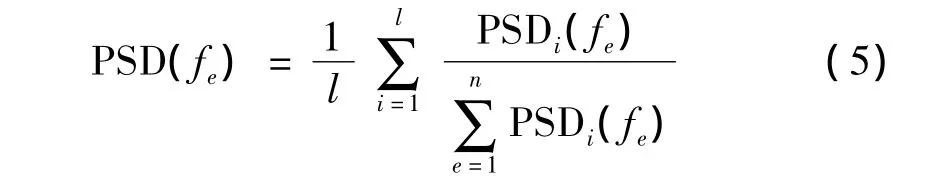
式中:fe为第e个频率，PSDi为第i测点功率谱密度函数，l为测点总数。可以看出，式(5)将所有测点功率谱密度进行了合成，为多测点模态参数识别提供了便利。

用此法进行模态参数识别时，需先确定参考点，参考点选择对参数识别结果影响较大，应尽量选择在各阶模态下响应均较大的点。环境监测数据中由于不可避免会混入噪声，因此需在运算前进行数据处理。

1.2 网架算例

建立正交正放四角锥网架结构有限元模型作为仿真算例，如图1所示。网格尺寸、网架截面高度均为3 m，上、下弦杆及斜杆截面积分别为17.17×10－4m2，13.08 ×10－4m2，7.9 ×10－4m2，节点质量 900 kg。用ANSYS中的Link8单元模拟杆件，mass21单元模拟节点重量，约束长度方向两侧上弦节点。

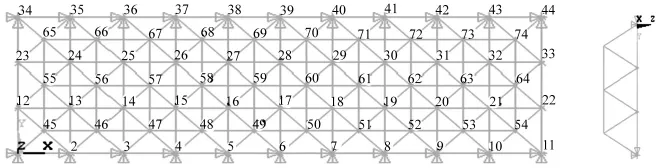
图1 网架模型Fig.1 Truss model

选择Block Lanczos方法进行模态分析，前6阶固有频率及振型如图2所示，第1阶振型为纵向平动，第2、3阶分别为纵向两端正对称与反对称竖向弯曲振型，第4、6阶分别为竖向弯曲正对称与反对称振型，第5阶为扭转振型。

图2 网架理论振型Fig.2 Truss mode shape

在结构上弦节点输入竖向白噪声激励，提取节点加速度信号。为更好模拟环境激励，在加速度信号中叠加了10%正态分布的随机白噪声，噪声模拟公式为:

式中:γi，i分别为无噪及有噪的加速度信号，εi为正态分布的随机数(均值为零，均方值为1)，P为在加速度信号上所加噪声。

加入噪声后需对其进行滤波［7］。目标模态为前6阶，选取测点12、13、24、32进行分析，图3中红色曲线为平均正则化功率谱。考虑理论分析与实际结构会存在差异，本文设定误差范围为5%，实测值与理论值对比在误差范围内即认为对应的频率，图4为理论值与实测值符合报告数据。

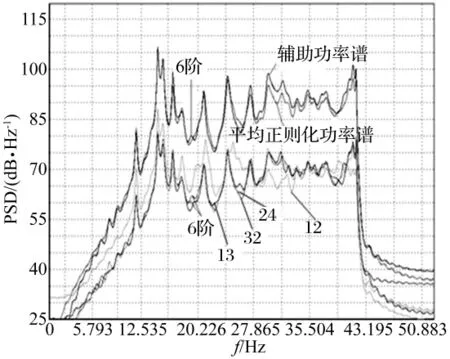
图3 功率谱曲线Fig.3 Power spectrum curve

图4 全部测点平均正则化功率谱A的符合报告Fig.4 The average regularization power spectrum of all channels(A)

综上可得:

(1)图4中识别出的前5阶频率，说明该方法具有较强的鲁棒性;

(2)图3全部测点正则化功率谱(红色曲线)第6阶频率未被识别。由图2知，分析用测点12、32恰好在第6阶振型节点附近，振动不明显，导致平均正则化功率谱丢失此波峰。即选择测点不恰当时，形成的平均正则化功率谱易遗漏模态;

(3)图4中第2阶理论频率15.092 Hz对应14.765 625 Hz，15.483 398 Hz两实测值。原因为空间网格结构自振频率密集，导致设定的5%误差搜索实测频率时“误中目标”，出现频率重叠。第4阶理论频率情况与其类似。

2 改进的功率谱峰值法

上述分析表明，尽管可利用平均正则化功率谱选取峰值以含所有测点信息，但对空间网格结构仍会出现模态遗漏与频率重叠。由于结构有限元分析所得理论振型能较好地反映结构振动特性，本文结合理论振型特点对功率谱峰值法进行改进。

2.1 辅助正则化功率谱

在形成全部测点平均正则化功率谱A的同时，据理论振型特点选择尽量远离各阶振型节点的测点计算辅助正则化功率谱B。

网架算例中，选择测点13、24形成辅助正则化功率谱曲线(图3黑色曲线)，即可识别出采用全部测点正则化功率谱A时遗漏的第6阶频率，如图5所示。

图5 辅助功率谱B的符合报告Fig.5 The results of auxiliary power spectrum(B)

2.2 相位准则

选择与重叠频率对应理论振型的两测点，按式(4)计算相位角，并分析相位关系。与理论振型中两测点相位关系不同的即非对应频率。

以全部测点平均正则化功率谱A为例，图4中，第2阶理论频率15.092 Hz对应两个实测值，取测点13、32计算相位角，14.77 Hz对应的相位角为0.01 rad(正相位)，15.48 Hz为 －3.01 rad(反相位)。由图 2 可知第2阶理论振型中两测点相位关系为正相位，因此所得15.48 Hz为虚假模态，得第2阶频率为14.77 Hz。

图4中，第4阶理论频率17.481 Hz对应两个实测值，仍取测点13、32 计算相位角，16.84 Hz与 18.05 Hz分别对应0.3 rad(正相位)、0.15 rad(正相位)。由图2可知第4阶理论振型中两测点相位关系为正相位，因此尚不能判定哪个是对应的第4阶频率，如图6所示。

图6 相位准则筛选后的结果(A’)Fig.6 The filter results after phase guidelines

2.3 振型准则

据所需判定的理论振型选择振型分量较大处对应的测点，计算该测点自谱，所得自谱中该振型具有明显的峰值。

针对网架第4阶重叠频率的筛选问题，取测点28计算自谱(图7)，该点处于3、5阶振型节点，但第4阶振型中振型分量明显较大，因此得第4阶频率为16.82 Hz，如图8所示。由于图4中16.84 Hz与此处16.82 Hz是由4个测点平均正则化及单测点功率谱分析所得结果差异较小，可忽略，而图4中18.05 Hz为虚假模态被排除。

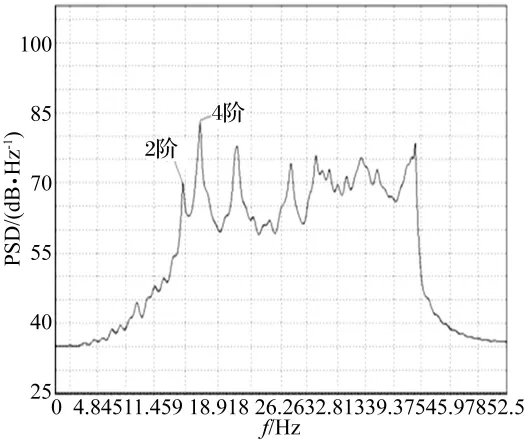
图7 振型节点28功率谱曲线Fig.7 Power spectrum curve of 28

图8 节点28频率识别结果Fig.8 Frequency identification result of 28

2.4 并集与结果整理

取平均正则化功率谱A与辅助正则化功率谱B的并集C，即将图4、5组合(图9)。若有重叠频率，则采用相位准则判别。若仍有重叠频率不能筛选，则采用振型准则判别，整理过程中忽略各次识别结果的微小差异。

图9 A与B的并集C Fig.9 The union of A and B

至此得前6阶频率识别结果如表1所示。网架前6阶模态频率最大相对误差为3.8%，频率识别精度较高，表明改进的功率谱峰值法能识别密集频率。

以节点13为参考点，所得该网架算例12～22节点前4阶竖向振型如图10所示。除个别节点略有误差外，整个振型轮廓比较相符。但通过该方法所得并非真正振型，而是工作挠度曲线形状，低阶振型识别结果误差较小，高阶误差较大。

表1 理论值与识别值对比(Hz)Tab.1 Comparison of theoretical and identification value(Hz)

图10 前4阶理论振型与识别振型对比Fig.10 The first four order contrast of theory and identify vibration mode

结合结构理论模态后，改进的功率谱峰值法计算流程如图11所示。

3 大运会主场馆振动监测应用

深圳市大运中心体育场钢屋盖结构体系为单层折面空间网格结构，如图12所示。该工程属于创新结构体系，传力路径曲折，受力复杂［8］。由于深圳是海滨城市，台风肆虐。要求在运营阶段进行监测，及时发现结构响应的异常、结构损伤或退化，确保结构安全［9］。

由Midas Gen ver7.0软件计算结果优化布置测点如图13所示，X、Y、Z分别代表三监测方向传感器。

3.1 频率识别

据监测方案，屋盖振动监测目标为前6阶频率及前4阶振型，为便于论述，选择局部的折面肋杆进行分析。取测点13、14、15、16的X向传感器数据计算，以14X为参考点，设定误差范围为5%，所得平均正则化功率谱A，如图14中红色曲线。用14X、15X测点功率谱曲线得到辅助正则化功率谱B，如图14中黑色曲线。两者与理论振型的符合报告见图15、图16，可看出辅助正则化功率谱B识别出A中遗漏了第3阶频率0.956 Hz。

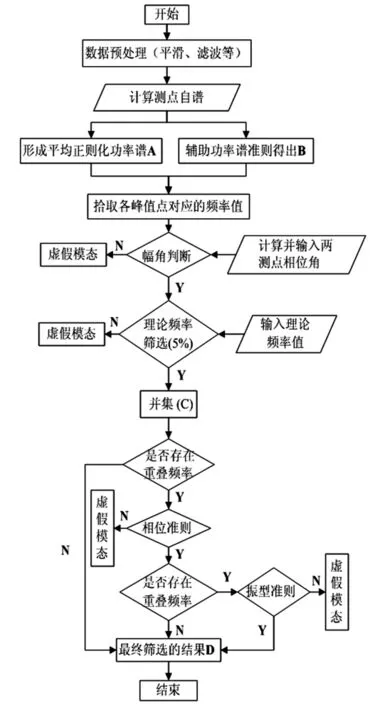
图11 计算流程图Fig.11 Program flowing chart

图12 大运会主场馆Fig.12 The main stadium

图17为取A与B并集后结果。利用相位、振型准则所得最终结果见表2。由表2知，所测前8阶频率值中，第7阶未被识别出。因此，含噪声数据模态参数识别中，某些模态常被噪声淹没而识别不出［10］，与所选测点在此阶振动节点附近有关。

对比表2数据看出，钢屋盖前8阶频率除第7阶外全部被识别出，最大相对误差为4.52%，频率识别精度较高，且满足监测方案要求(前6阶)，有较大工程应用价值。

图13 振动测点布置方案Fig.13 Vibration measuring point layout program

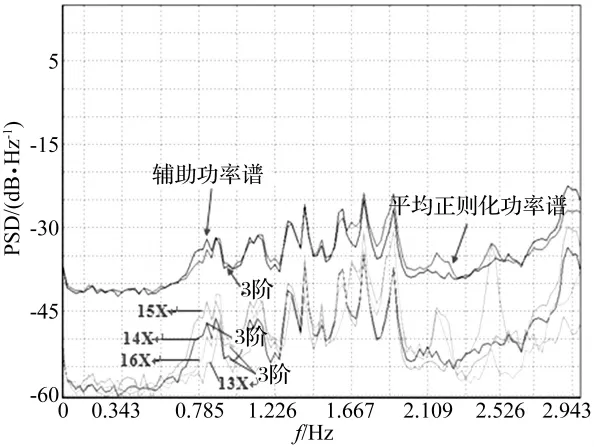
图14 功率谱曲线Fig.14 Power spectrum curve

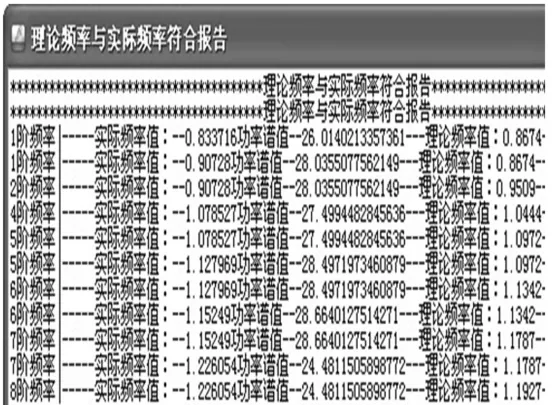
图15 全部测点平均正则化功率谱A Fig.15 The average regularization power spectrum of all channels(A)

表2 理论值与识别值对比(Hz)Tab.2 Comparison of theoretical and identification value(Hz)

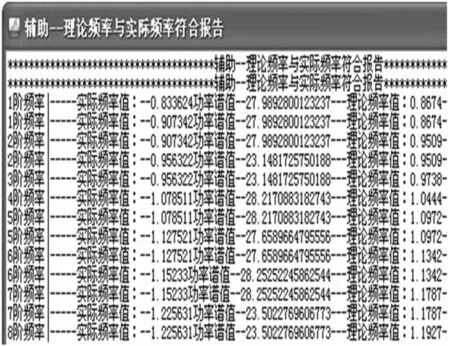
图16 辅助功率谱B Fig.16 The results after auxiliary power spectrum(B)

图17 A与B的并集C Fig.17 The union of A and B

3.2 振型识别

由理论振型及实测可得，第1、2阶相似，第3、4阶相似，因此本文仅给出第1阶及第4阶识别结果，如图18、图19所示。

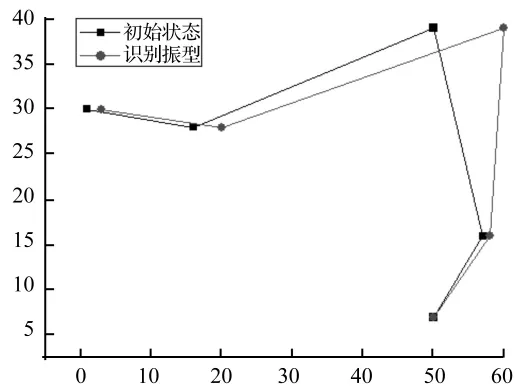
图18 第1阶振型识别图Fig.18 First-order mode shape identification

从振型图可得出，除个别节点(14X)外，其他三测点误差较小，整个振型轮廓较相符。

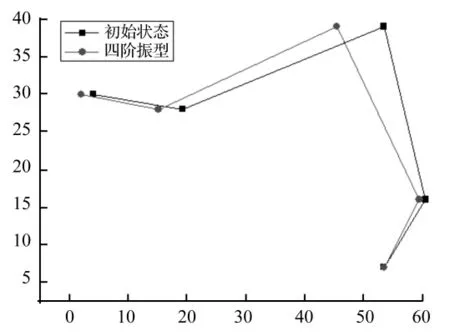
图19 第4阶振型识别图Fig.19 Four-order mode o shape identification

4 结论

针对空间网格结构模态密集特点，结合理论振型特征提出改进的功率谱峰值法，结论如下:

(1)采取辅助正则化功率谱及相位准则、振型准则的判别策略可较好地避免模态遗漏及重叠频率识别;

(2)通过大运会主场馆监测的应用验证了改进的功率谱峰值法的有效性;

(3)对实际工程进行模态识别时，需建立结构精确有限元模型用以分析，选取远离目标模态节点处的测点，同时需确保获得良好的测试数据，信噪比过低将导致无法识别。

［1］Liu C W，Wu J Z，Zhang Y G.Review and prospect on modal parameter identification of spatial lattice structure based on ambient excitation［J］.Applied Mechanics and Materials，2011:94 －96:1271 －1277.

［2］谢献忠，陈文新，钟新谷，等.环境激励下湘潭莲城大桥模态参数识别研究［J］.湖南科技大学学报(自然科学版)，2008，23(4):53－56.XIE Xian-zhong，CHEN Wen-xin，ZHONG Xin-gu，et al.Study on identification of modal parameters of liancheng bridge of xiangtan based on ambient excitation［J］.Journal of Hunan University of Science＆Technology(Natural Science Edition)，2008，23(4):53－56.

［3］姜 浩，郭学东，杨焕龙.预应力混凝土桥梁模态参数识别方法［J］.沈阳建筑大学学报(自然科学版)，2009，25(9):915－919.JIANG Hao，GUO Xue-dong，YANG Huan-long.Research on modal identification method of pre-stressed concrete bridge［J］.Journal of Shenyang Jianzhu University(Natural Science)，2009，25(9):915－919.

［4］王锦文.深圳市民中心屋顶网架结构的有限元模型修正及模态参数识别［D］.武汉:武汉理工大学，2004.

［5］郑毅敏，孙华华，赵 昕，等.大跨度高空钢结构连廊的有限元模型修正［J］.振动工程学报，2009，22(1):105－110.ZHENG Yi-min，SUN Hua-hua，ZHAO Xin，et al.Finite element model updating of a long-span steel skybridge ［J］.Journal of Vibration Engineering，2009，22(1):105－110.

［6］张爱林，王冬梅，刘学春，等.2008奥运会羽毛球馆弦支穹顶结构模型动力特性试验及理论分析［J］.建筑结构学报，2007，28(6):69 －75.ZHANG Ai-lin，WANG Dong-mei，LIU Xue-chun，et al.Dynamic performance experiment and theoretical analysis on the suspend-dome structure model of the badminton gymnasium for 2008 Olympic Games［J］.Journal of Building Structure，2007，28(6):69－75.

［7］杨绿溪.现代数字信号处理［M］.北京:科学出版社，2007:217－218.

［8］刘琼祥，张建军，郭满良，等.深圳大运中心体育场钢屋盖设计难点与分析［J］.建筑结构学报，2011，32(5):39－47.LIU Qiong-xiang，ZHANG Jian-jun，GUO Man-liang，et al.Analysis and design challenge of steel roof of the Shenzhen universiade sports centre［J］.Journal of Building Structure，2011，32(5):39－47.

［9］范 峰，王化杰，金晓飞，等.超高层施工监测系统的研发与应用［J］.建筑结构学报，2011，32(7):50－59.FAN Feng， WANG Hua-jie， JIN Xiao-fei， etal.Developmentand application ofconstruction monitoring system for super high-rise buildings［J］.Journal of Building Structures，2011，32(7):50 －59.

［10］刘 会，张亮亮，杨转运，等.采用不同方法识别结构模态参数的比较［J］.重庆大学学报，2010，33(6)，60－66.LIU Hui，ZHANG Liang-liang，YANG Zhuan-yun，et al.Comparative study on the identification of structural modal parameter using different methods［J］.Journal of Chongqing University，2010，33(6):60－66.