改进的结构振动传递矩阵法

万浩川，李以农，郑 玲

(1.重庆大学 机械传动国家重点实验室，重庆 400044;2.乐山职业技术学院，四川 乐山 614000)

传递矩阵法自上世纪20年代提出，于60～70年代在结构振动中广泛应用［1］。传递矩阵法最初用于薄壳结构的自由振动分析，但精度较低。向宇［2］运用微分方程与矩阵分析理论，将传递矩阵表示成封闭形式，直接得出传递矩阵的精确形式，大大提高了传递矩阵法的计算精度。因此传递矩阵法被广泛应用于钢桥结构分析［3］、转子系统振动分析［4］、轴系扭振［5－7］、旋转壳振动［8］等领域。

若将结构控制微分方程写成一阶微分方程组的形式，则起点与终点的状态向量间即可用传递矩阵建立简单关系，利用边界条件可得问题答案。因此，传递矩阵法计算精度主要取决于状态向量的选取与矩阵方程的积分。动力方程积分方法研究较多，如精细时程积分法［9－12］、龙格库塔法［13－14］、齐次扩容积分法［15］。随着计算机技术的发展，积分计算精度不断提高，已基本能满足要求。而随着传递矩阵法在多自由度系统中的应用，状态向量一阶方程的推导却越加困难。因为之前研究基本根据边界条件确定状态向量，而状态向量并不能从振动方程中直接获得，造成状态向量一阶微分方程推导过程非常复杂，不仅工作量增加，且常有错误出现。

本文以圆柱壳与约束阻尼圆柱壳振动为例，对传递矩阵法进行改进，直接由振动方程选择状态向量，可减轻推导状态向量一阶导数的工作量。在状态向量与边界条件之间引入关联矩阵，并代入传递矩阵求解，在减少出错的同时可获得与原方法相同计算精度。

1 圆柱壳振动的改进传递矩阵法

1.1 圆柱壳振动方程

如图1所示，圆柱壳长L，半径R，厚度H。取圆柱壳体母线与纬线方向为正交曲线坐标系主方向。中面上一点坐标用(s，θ)表示，s为顶点至该点母线长度，θ定义同一般旋转壳。Ρ为材料密度、E为弹性模量，μ为泊松比。

图1 圆柱壳示意图Fig.1 A cylindrical shell

若壳体中曲面上一点的轴向、切向、法向位移分别为 u、v、w，则据克希霍夫假定［16］，圆柱壳振动方程为:

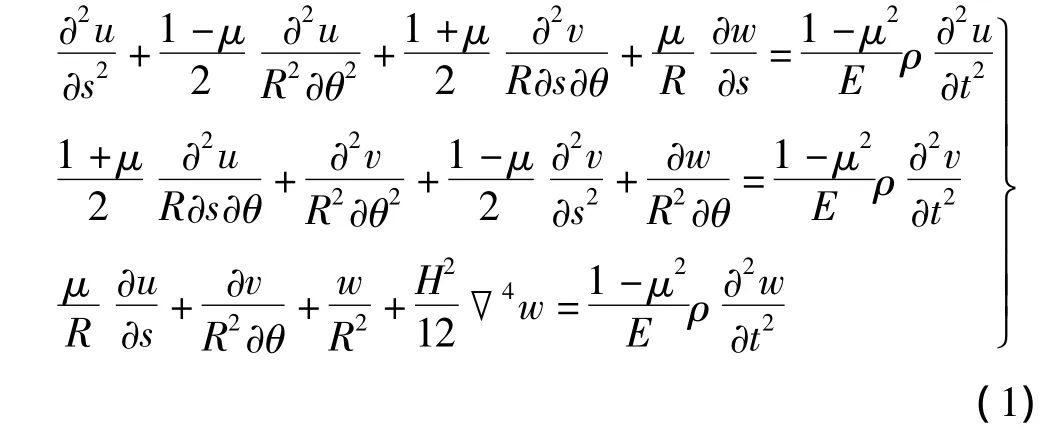
对轴向半波数为m、周向波数为n的振动模态，ωmn为固有频率，则式(1)的解可写为:

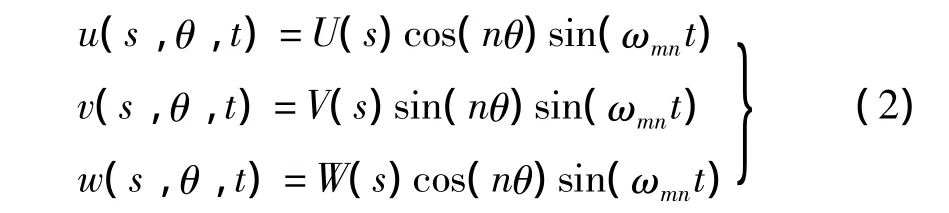
式中:U(s)，V(s)，W(s)分别为轴向位置s的函数。将式(2)代入式(1)，并化简得:

1.2 传递矩阵

圆柱壳边界条件为:

文献［8，16］均将边界条件向量 ζ={U，V，W，φ，N，F，S，M}设为状态向量，虽解方程容易，但状态向量的一阶微分计算较复杂，且易出错。本文选ξ=为状态向量，其一阶微分可直接由式(3)获得:八阶矩阵C中的非零元素为:

由式(4)可得ζ=Dξ，八阶矩阵D中非零元素为:

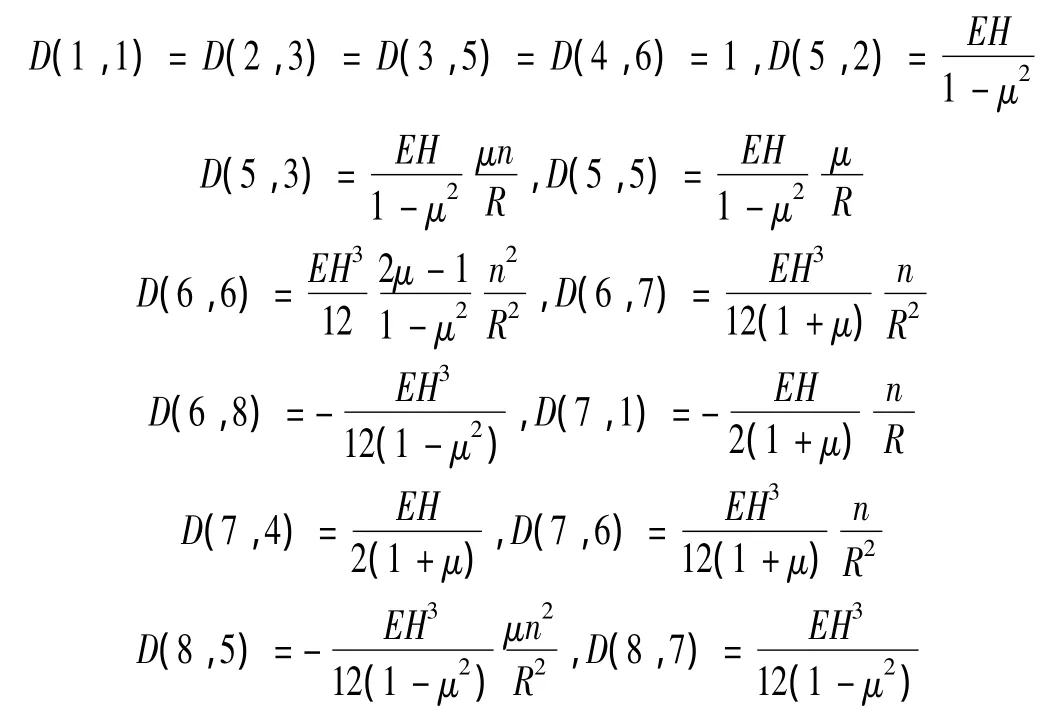
称D为状态向量与边界条件之间的关联矩阵。有:ζ(s)=Dξ(s)=DeCsξ(0)=DeCsD－1Dξ(0)=DeCsD－1ζ(0)令:T=DeCsD－1，有:ζ(s)=Tζ(0)，其中 T 为传递矩阵。通过引入关联矩阵D，使其求解更简单。

1.3 方程求解

以两端简支边界为例:

ζ(L)=［U(L)，0，0，φ(L)，0，F(L)，Ss(L)，0］ζ(0)=［U(0)，0，0，φ(0)，0，F(0)，S(0)，0］

有:

令:

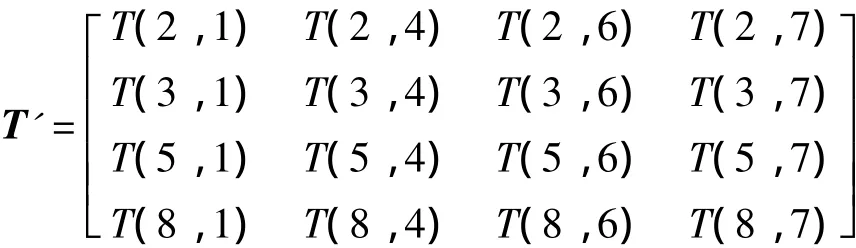
式(5)有非零解条件为T'=0。而T'为频率函数。由此可得各阶模态固有频率值。对不同的边界约束，可得不同的T'，但均T'=0。

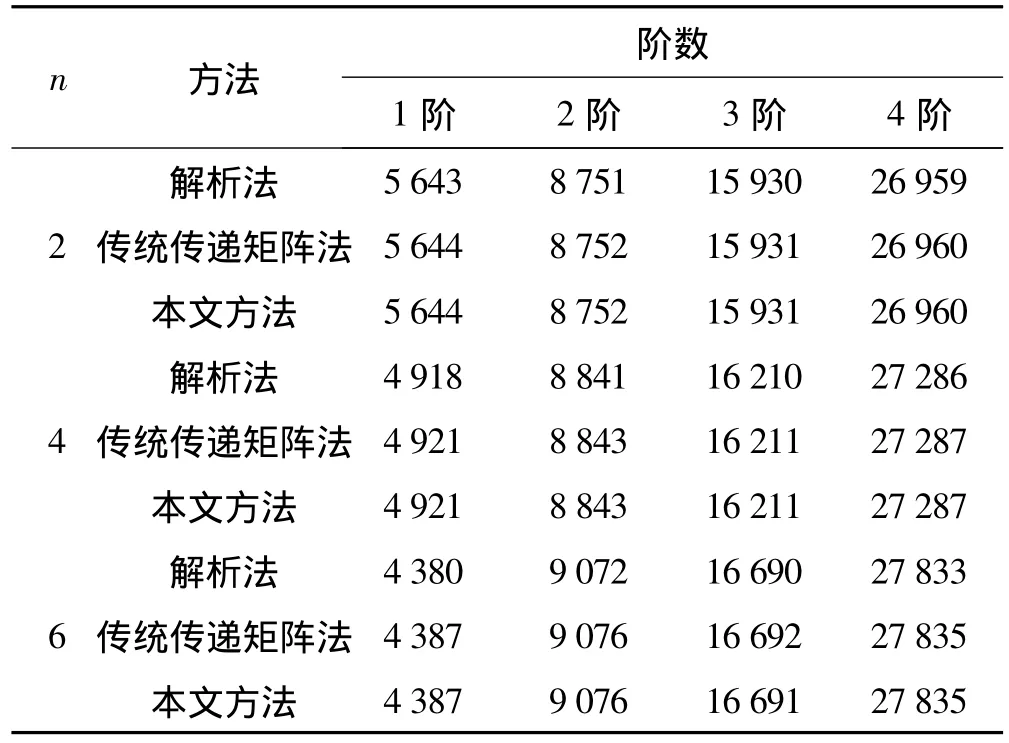
表1 两端简支鼓筒固有频率计算结果(m=0)Tab.1 Natural frequency shell by different methods

1.4 算例

为验证计算方法与计算程序的正确性，对具有解析解的两端简支柱壳进行计算。圆柱壳尺寸与材料参数为(单位均为国际标准单位):L=0.06，R=0.142 7，H=0.002 4，E=2.1E+11，μ =0.3，ρ=7 850 。

两端简支、n取不同值时采用解析法与传递矩阵法所得固有频率f(Hz)见表1。

由表1看出，本文改进的传递矩阵法因原理完全一致，计算精度未受任何影响。

2 约束阻尼圆柱壳振动的改进传递矩阵法

2.1 约束阻尼圆柱壳振动方程

将克希霍夫假定引入约束阻尼圆柱壳，并忽略粘弹层拉伸变形，可得约束阻尼圆柱壳振动方程为［17］:

式(6)各变量定义同前，下标1、2、3分别代表基层、粘弹层、约束层。其它变量见文献［17］。其解的形式为:

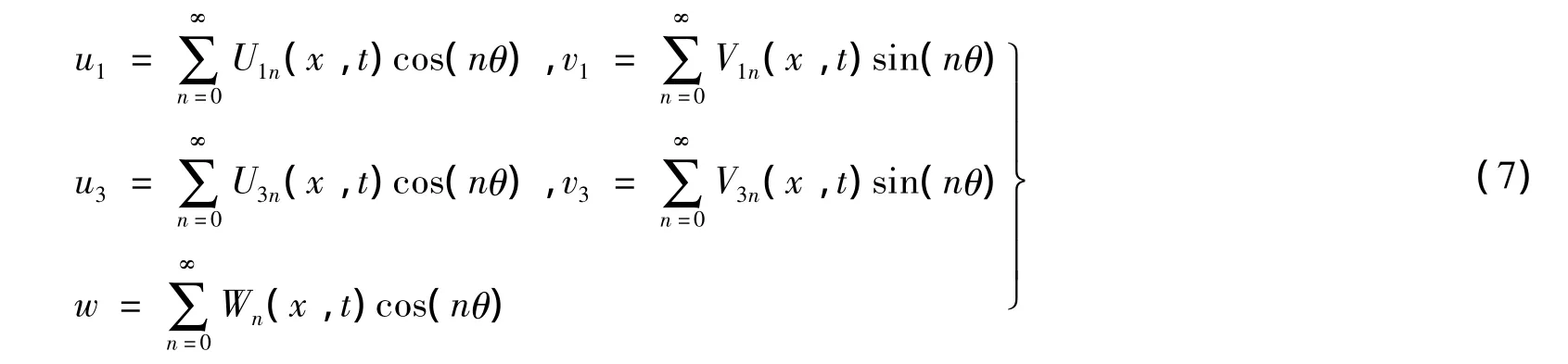
2.2 传递矩阵

将式(7)代入式(6)，得:

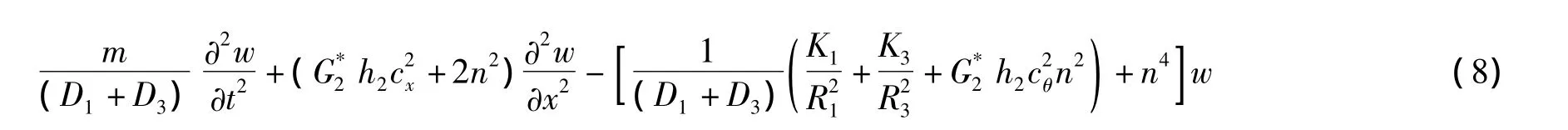
边界条件为:

十二阶矩阵C中非零元素为:

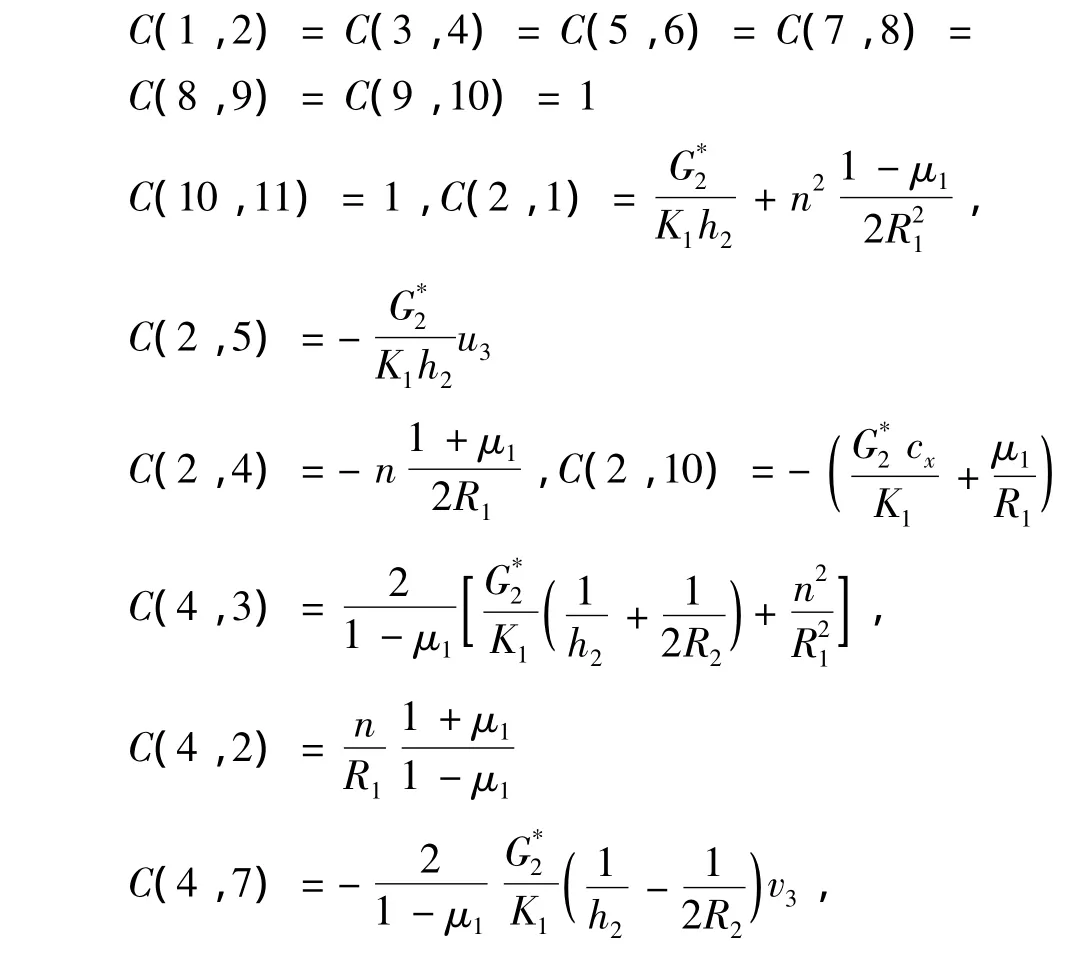
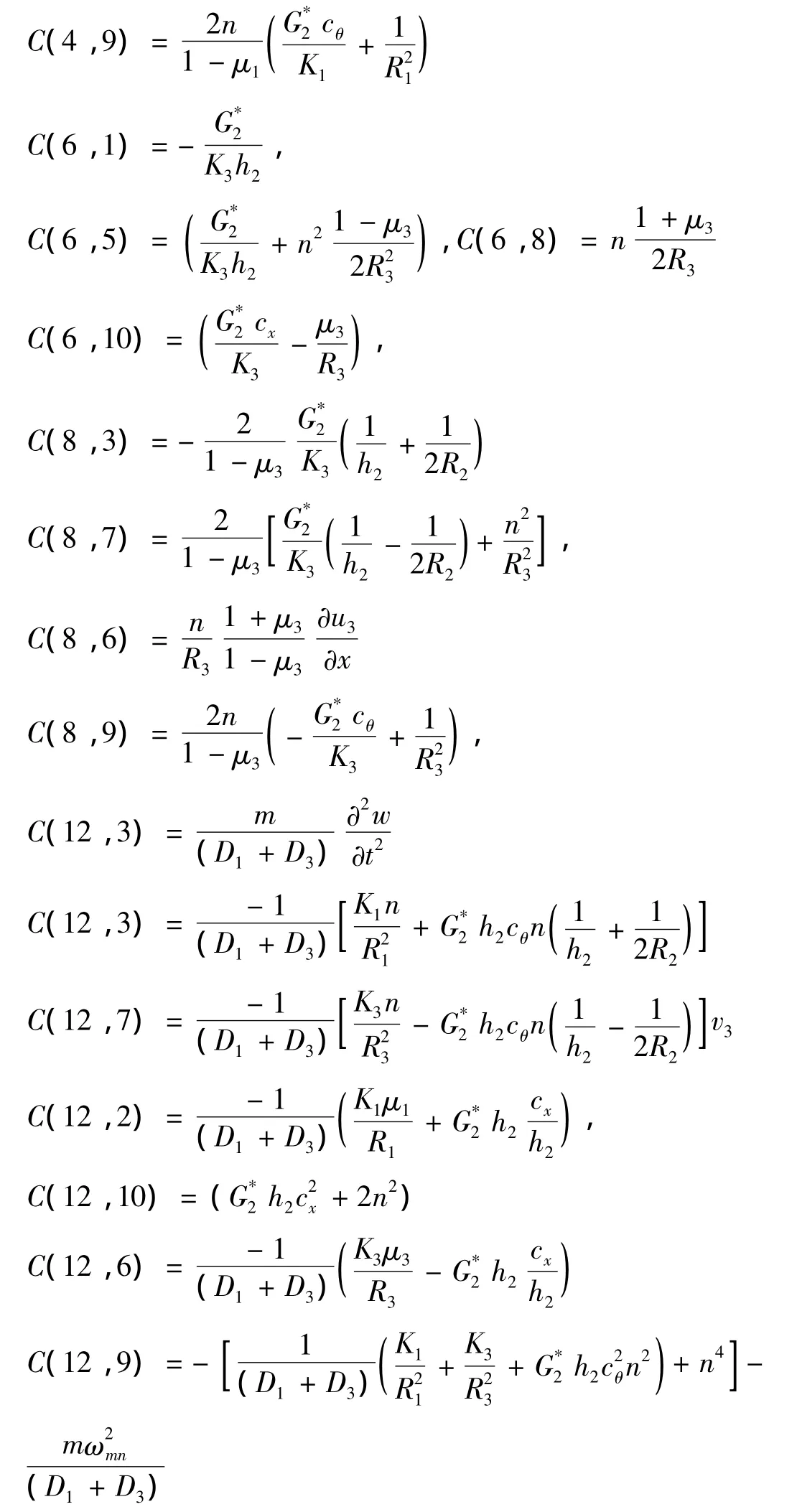
十二阶矩阵D中的非零元素为:

由运算可较易获得传递矩阵T。

2.3 方程求解

与圆柱壳求解相同，据边界条件选择传递矩阵子矩阵T’，并令其行列式为零，即可求解。

2.4 算例

取约束阻尼圆柱壳基层［17］为:半径 R1=0.3 m，长L=0.1 m，hl=0.003 m，h2=0.001 m，h3=0.002 m，El=E3=70 GPa，ρl= ρ3=2 700 kg/m3，μl= μ3=0.3，G2*=0.896(1+0.968 3i)MPa，ρ2=999 kg/m3，边界条件为两端固支:

本文解与文献［17］解的对比见表2。由表2看出本文方法计算结果非常精确。

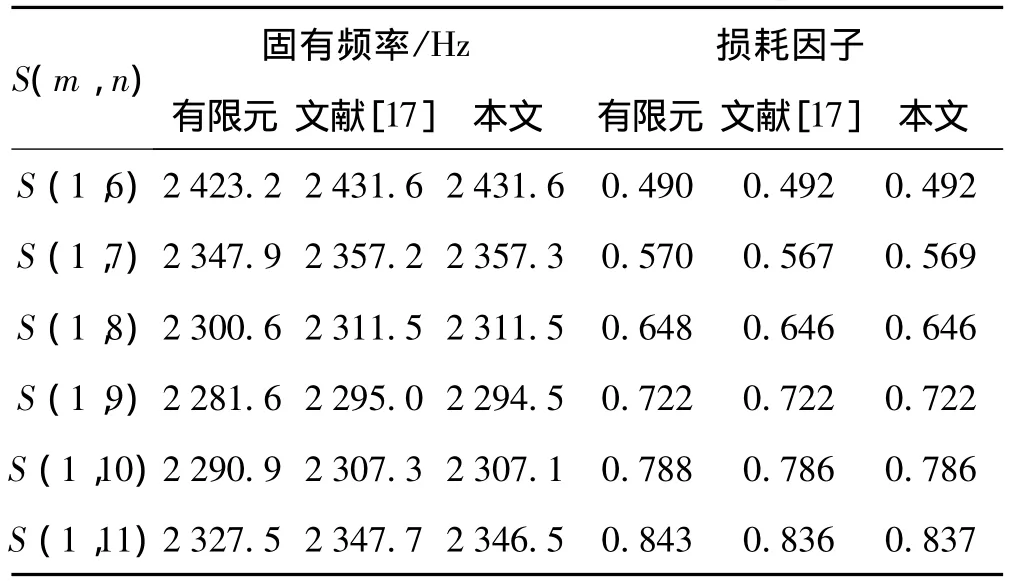
表2 约束阻尼壳动力学特性计算结果对比Tab.2 Dynamic results of constrained damping shell

3 结论

(1)通过对状态向量选取进行改进，可简化一阶导数求解。通过关联矩阵将状态向量与边界条件相联系，可使传递矩阵计算更简单，从而简化方程的求解过程。

(2)本文方法通过算例证明其正确性。尤其求解方程较复杂的多自由度振动系统优点更明显。对传递矩阵法应用于更多领域具较好的推广作用。

［1］朱静清.结构振动计算中传递矩阵法的应用问题［J］.地震工程与工程振动，1984，4(1):36 －44.ZHU Jing-qing.Application problems of the transfer matrix method in calculating the vibration of structures［J］.Journal of Earthquake Engineering and Engineering Vibration，1984，4(1):36－44.

［2］向 宇.分析结构自由振动的传递矩阵精确形式［J］.振动与冲击，1999，18(2):69 －74.XIANG Yu.The exact form of transfer matrix for analysis of free vibration of structures［J］.Journal of Vibration and Shock，1999，18(2):69－74.

［3］张 杰.传递矩阵法在钢桥结构分析中的应用研究［D］.南京:河海大学，2005.

［4］刚宪约.多转子系统振动分析的整体传递矩阵法研究［D］.大连:大连理工大学，2002.

［5］陈奎孚，彭洪涛，焦群英.复杂传动轴系扭振的递归传递矩阵法［J］.农业工程学报，1999，15(2):42 －45.CHEN Kui-fu， PENG Hong-tao， JIAO Qun-ying. The recursive transfer matrix method to calculate the torsional vibration of complex transmission system［J］.Transactions of the Chinese Society of Agricultural Engineering， 1999，15(2):42－45.

［6］孟 杰，陈小安.电主轴动力学分析的传递矩阵法［J］.机械设计，2008，25(7):37 －40.MENG Jie，CHEN Xiao-an.Transference matrix method for dynamics of motorized spindle［J］.Journal of Machine Design，2008，25(7):37 －40.

［7］冯栋梁，魏来生.传递矩阵法在动力传动系统扭振分析中的应用［J］.车辆与动力技术，2010(1):41－45.FENG Dong-liang，WEI Lai-sheng.Application of transfer matrix method in vehicle power train’s torsional vibration analysis［J］.Vehicle ＆ Power Technology，2010(1):41－45.

［8］苏海东，黄玉盈.分析旋转薄壳的传递矩阵法［J］.工程力学，2008，25(9):1 －6.SU Hai-dong，HUANG Yu-ying.A transfer matrix method for analyzing revolutionary shells［J］.Engineering Mechanics，2008，25(9):1 －6.

［9］钟万勰.结构动力方程的精细时程积分法［J］.大连理工大学学报，1994，34(2):131 －136.ZHONG Wan-xie.On precise time-integration method for structural dynamics［J］.Journal of Dalian University of Technology，1994，34(2):131 －136.

［10］张洪武.关于动力分析精细积分算法精度的讨论［J］.力学学报，2001，33(6):847 －852.ZHANG Hong-wu.Discussion on the accuracy of precise integration method in dynamic analysis［J］.Acta Mechanic Sinica，2001，33(6):847 －852.

［11］王 忠，王雅琳，王 芳.任意激励下结构动力响应的状态方程精细积分［J］.计算力学学报，2002，19(4):419－422.WANG Zhong，WANG Ya-lin，WANG Fang.A high precise integration scheme for structural dynamics analysis under arbitrary excitation［J］.Journal of Computational Mechanics，2002，19(4):419－422.

［12］李青宁，李晓雷，阎艳伟.结构动力方程精细时程积分法的几种改进［J］.西安建筑科技大学学报，2009，41(1):6－10.LI Qing-ning，LI Xiao-lei，YAN Yan-wei.Improvement on the structural dynamic equation precise time-integration［J］.Journal of Xi’an University of Architecture and Technology，2009，41(1):6 －10.

［13］Zhang S Y，Deng Z C，Li W C.A precise Rutta-Kutta integration and its application for solving nonlinear dynamical systems［J］.Applied Mathematics and Computation，2007，184:496－502.

［14］富明慧，梁华力.一种改进的精细－龙格库塔法［J］.中山大学学报(自然科学版)，2009，48(5):1 －5.FU Ming-hui，LIANG Hua-li.A improved precise rungekutta integration［J］Acta Scientiarum Naturalum Universities Sunyatseni，2009，48(5):1 － 5.

［15］Xiang Y，Huang Y Y.A semi-analytical and semi-numerical method for solving 2－D sound-structure interaction problems［J］.Acta Mechanica Solida Sinica，2003，16(2):1l6 －126.

［16］晏砺堂.结构系统动力特性分析［M］.北京:北京航空航天大学出版社，1989.

［17］李恩奇，李道奎，唐国金，等.约束阻尼圆柱壳动力学分析［J］.工程力学，2008，25(5):6 －11.LI En-qi， LI Dao-kui， TANG Guo-jin， et al. Dynamic analysis of constrained layer damping cylindrical shell［J］.2008，25(5):6 －11.