基于最小二乘支持向量机的结构地震响应时滞控制算法

赵德奇，李春祥，蓝声宁

(1.上海大学 土木工程系，上海 200072;2.湖南科技大学 土木工程学院，湖南湘潭 411201)

主动控制系统受时滞影响控制效果大大减弱。时滞影响因素［1］主要有:① 液压系统或电机系统执行控制动作所需时间;② 结构反应从传感器到控制器传递时间及计算控制力所耗时间。因此，如何进行时滞补偿以减小时滞对主动控制效果影响为需探究问题。文献［2-7］提出众多时滞补偿算法，大致可分三种类型:理论型补偿、相空间补偿及时域补偿。理论型时滞补偿一般在时滞较小情况下效果较好;时滞较大时，需提供较大控制力。实际控制系统可能出现较大时滞时，为获得与无时滞相同控制效果，需大幅提高控制力，既不经济又不实用。相空间补偿方法前提为准确获得延迟状态参量与结构主频率。运用不正确的主频率会导致结构不稳定［6］。针对地震作用，通过预测系统状态向量或反馈增益实现时域补偿更具有实用性。因此，本文将线性二次型控制(Linear Quadratic Regulator，LQR)与最小二乘支持向量机(Least Squares Support Vector Machines，LSSVM)进行集成，建立时滞LSSVMLQR算法。

支持向量机(Support Vector Machines，SVM)是由Vapnik［8］提出的一种学习算法。SVM在分类与回归方面具有优势，为解决时滞问题提供了新思路。SVM专门针对有限样本情况的学习机器，可实现结构风险最小化，将实际问题通过非线性变换转换到高维特征空间，在高维空间中构造线性决策从而实现原空间中的非线性决策函数，巧妙解决了维数问题［9］;同时也克服了神经网络存在的过学习与局部极值点的缺陷，具有小样本学习、全局寻优、泛化能力强等特点［10］。然而，在解决大样本问题时，SVM由于迭代误差积累而无法满足精度要求。为此，Suykens等［11］提出新型的支持向量机—最小二乘支持向量机 (LSSVM)。LSSVM将支持向量机中目标函数不等式约束改为等式约束，将求解二次规划问题转化成求解线性方程组，并将经验风险由偏差一次方改为二次方，避免了不敏感损失函数，大大降低了复杂度，并解决了其中存在的鲁棒性、稀疏性及大规模运算问题，运算速度高于一般的SVM，在非线性预测控制中更具优势。在本文时滞LSSVMLQR算法中，运用LQR算法计算结构所需最优控制力，并设为目标控制力;采用LSSVM对其进行训练学习，对目标控制力进行回归预测。取t为结构滞后时间，采用LSSVM回归预测t时刻后的目标控制力，并实时控制驱动力装置产生的控制力对结构进行及时控制。

1 最小二乘支持向量机(LSSVM)原理

对给定的学习样本集(xi，yi)，xi∈Rn，yi∈R，(i=1，…，n)，xi为n维输入向量，yi为一维输出。在高维特征空间中构造最优线性函数:

式中:φ为输入空间Rn到高维特征空间的非线性映射;w，b为待求回归参数，w为权向量，b为阀值。

据结构风险最小化原理，并考虑函数复杂度及拟合误差，回归问题可表示为约束优化问题，即:

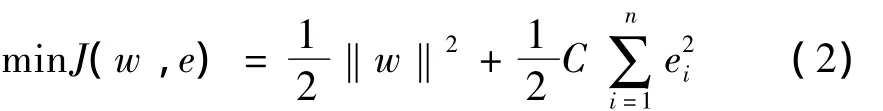
约束条件:

用Lagrange方法求解式(2):

式中:C为惩罚因子，α =(α1，α2，…，αn)为 Lagrange乘子。据KKT最优条件进行偏微分处理后所确定的决策函数为:

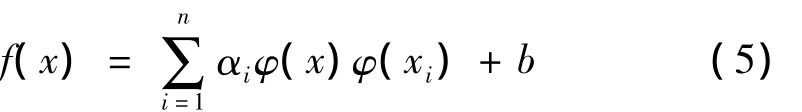
式中:α，b为求解线性方程组所得模型参数。定义核函数K(x，xi)=〈φ(x)φ(xi)〉，得:

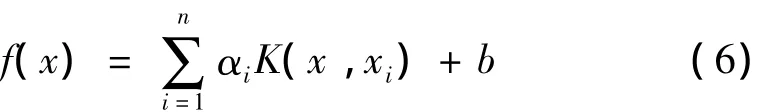
上述算法中核函数K(x，xi)为高维特征空间内积。引入核函数目的即由原始空间中抽取特征，将原始空间中样本映射为高维特征空间中的向量［12］，如图1所示。据泛函理论，只要满足Mercer条件的函数均可作为核函数，不同核函数构造出不同的支持向量机。目前，研究较多的有线性核函数、多项式核函数、高斯核函数及sigmoid核函数等。本文采用径向基(RBF)核函数:

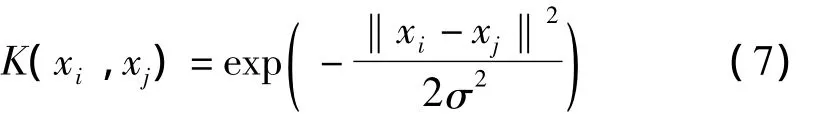
2 线性二次型最优控制(LQR)

2.1 连续状态模型

设各层安装主动控制装置的n自由度结构如图2所示，其运动方程为:

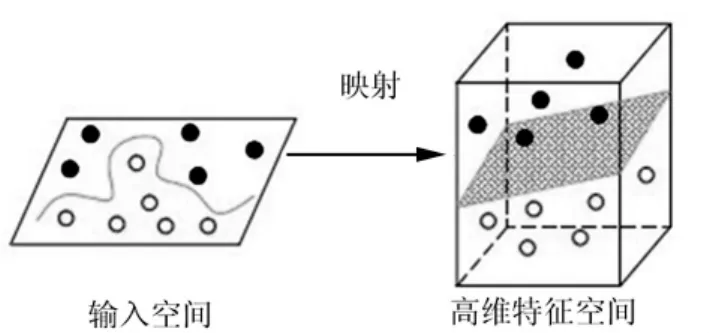
图1 输入空间映射到高维特征空间图Fig.1 Nonlinear mapping of input data into a high dimensional feature space

图2 结构主动控制系统Fig.2 Active control system for structures

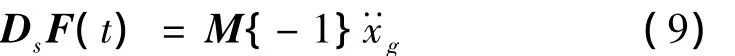
式中:{-1}为元素-1的列向量;为地震地面加速度。式(8)即为状态方程:

设作用在结构上的干扰仅有地震作用，即:

假设结构全部状态均能观测到，定义系统二次型泛函为:

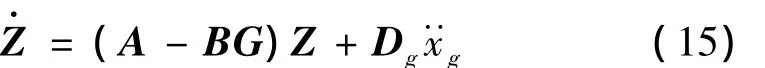
求解式(15)可得状态向量Z，代入式(14)可求得最优驱动力U。

2.2 离散状态模型

干扰荷载仅考虑地震作用时，结构控制系统离散状态方程可表示为:

式中:Z(k)，Z(k+1)分别为结构控制系统第k步(对应时间为t=k×Δt)与第k+1时刻的状态反应;U(k)为第k步主动控制力(k)为第k步地震输入;Ad，Bd，Dd分别为离散状态系统矩阵、控制力位置矩阵与干扰作用位置矩阵，可通过A，B，Dg求得。

考虑控制系统存在时滞时，需采用状态方程求解结构控制系统第k+1的状态反应，即:

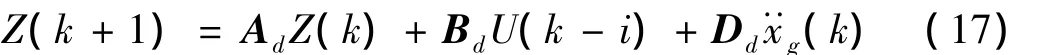
式中:i为时滞步长，对应iΔt的时滞。

将U(k-i)=-GZ(k-i)代入式(17)得:

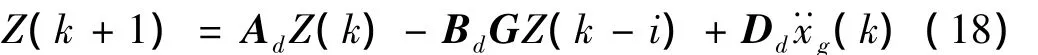
据结构初始位移及初始速度，用式(18)逐步迭代可求解结构控制系统的地震反应。

式中:Q，R分别为半正定及正定权矩阵，即结构控制系统中的控制参数。

在闭环控制情况下，即tf=∞时的所谓无限时间最优控制全状态反馈，据Riccati矩阵代数方程:

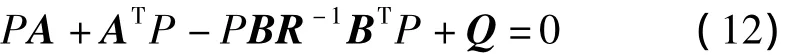
求出矩阵后，可得所需增益矩阵G:

进而得最优驱动力为:

得结构控制系统状态方程为:

3 时滞LSSVM-LQR控制算法

时间滞后导致结构主动控制不能及时对结构响应做出有效控制，大大降低了LQR最优控制效果，结构稳定性变差，甚至产生负反应。为此，将LSSVM引入LQR中，先对采集的最优控制力进行LSSVM训练，并回归预测第k步时最优控制力U^(k)，则第k+1步状态向量计算式为:

再由式(14)得:

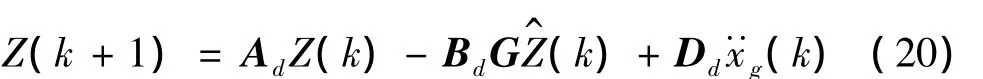
因此，对LQR最优控制力的学习训练及回归预测可转化为对结构系统状态向量的学习训练及回归预测。形成一个闭环控制，既可保证信息采集方便，亦可保证系统的循环性。时滞LQR控制系统与时滞LSSVM-LQR控制系统模块见图3。

图3 结构时滞LQR与时滞LSSVM-LQR控制系统模块Fig.3 Block diagram of LQR and SVM-LQR control systems with time-delay

LSSVM训练时，选取训练样本数量至关重要。训练样本量越大，训练速率越慢。故本文取定量数据作为训练样本，在保持训练效果的同时提高程序执行效率及速度。电脑配置:主板/ASUS P8P67、CPU/I7-2600 K 3.4 GHz、内存/3 GB，为考察算法训练效率，分别取50、100、150、200个数据作为样本进行训练，产生的时滞量见表1。

表1 算法训练效率Tab.1 Training efficiency of the algorithm

表1中数据显示，样本数量愈大，算法耗时越长。样本量达到某一值时算法预测的准确性已有保证。本文在综合考察预测效果与训练效率基础上选取100个数据作为训练样本。由于在初采集数据的一段时间里样本量较少，LSSVM回归预测效果会有较大误差，因此可约定样本量下限为10。样本量小于10时，不对驱动装置实施时滞补偿。LSSVM-LQR控制算法流程见图4。

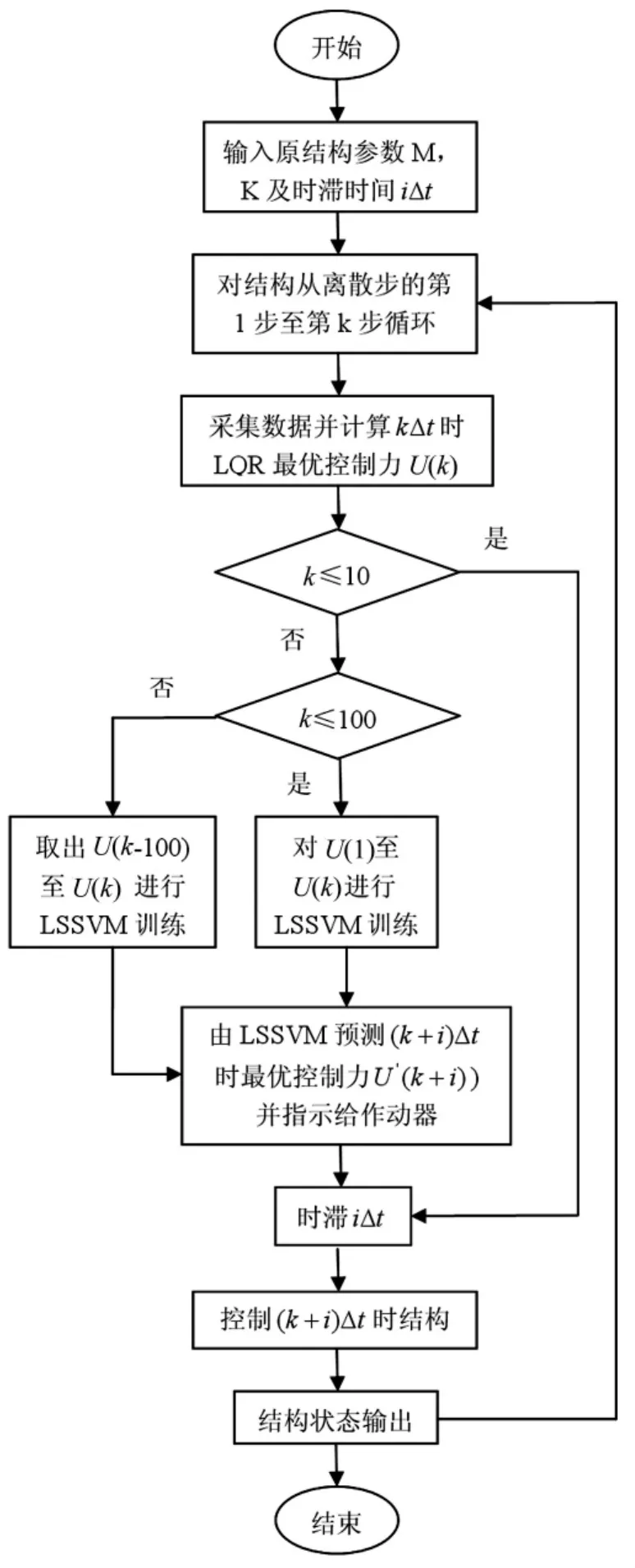
图4 LSSVM-LQR控制算法流程图Fig.4 Flowchart of the LSSVM-LQR control algorithm

4 LSSVM-LQR控制算法数值验证与比较

考虑3层框架结构，质量mi=2×106(kg)，层间刚度ki=1 ×109(N/m)(i=1，2，3)，其质量、刚度矩阵为:

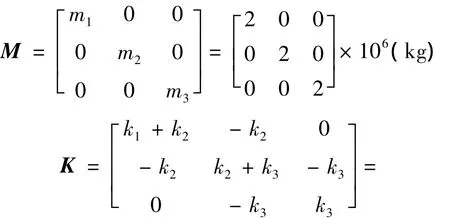
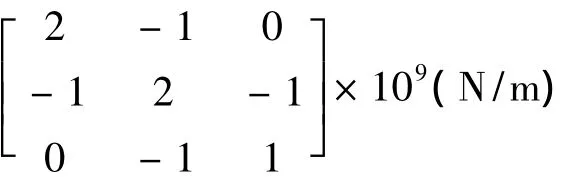
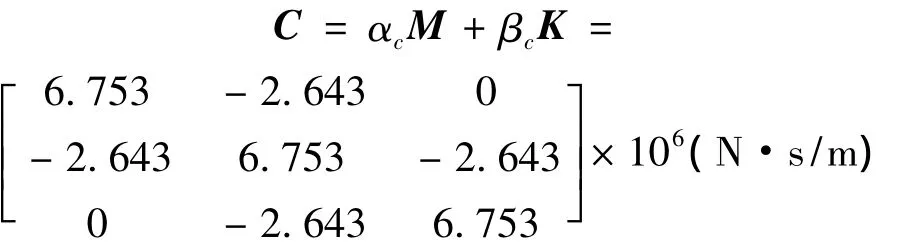
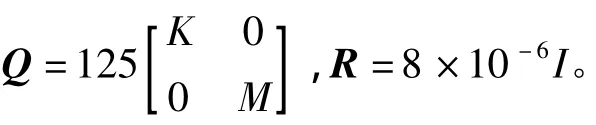
由表2～表5看出，时滞对结构控制效果产生不利影响，且随滞后时间的增长，控制效果越差。Taft波与上海人工波1在时滞达0.18 s时，因时滞而增大的结构响应约为60%，若不对时滞进行控制，必导致最终控制结果发散。采用时滞LSSVM-LQR算法对结构进行控制后，因时滞产生的不利影响得到明显改善。另外，由表中不难发现其规律:① 时滞较短时，时滞LSSVMLQR算法补偿效果较明显，不仅几乎完全弥补因时滞产生增大部分响应，甚至可减小到较无时滞时效果更好，因在循环迭代过程中好的补偿效果得以积累与加强;而随着时滞加长，时滞LSSVM-LQR算法补偿效果逐渐下降，因随着时滞的加长，预测效果下降，导致补偿效果下降，但依然保持较好的补偿效果。② 时滞LSSVM-LQR算法对峰值位移补偿效果较好，而对峰值加速度及最大控制力补偿效果稍差。因时滞LSSVM-LQR算法基于位移与速度进行反馈预测控制，即算法重点补偿了位移及速度因时滞产生的不利影响，因此对位移的补偿效果较好，而对加速度与控制力的补偿效果稍差。③ 时滞较短时，时滞LSSVM-LQR算法补偿效果的离散性较大。因时滞较短时，时滞对结构影响较小(即计算时滞补偿效果时分母较小)，时滞补偿效果对LSSVM预测数据敏感性较大，会出现最大时滞补偿达700%而最差的时滞补偿达-210%情形。④ 时滞LSSVM-LQR算法对四种波的补偿效果各不相同。主要原因为:与核函数形式的选取有一定相关性，不同波对同一种核函数敏感程度不同;核函数参数通过试算方式选取，因时间限制，所选参数不一定最优化。

图5 地震波Fig.5 Seismic waves

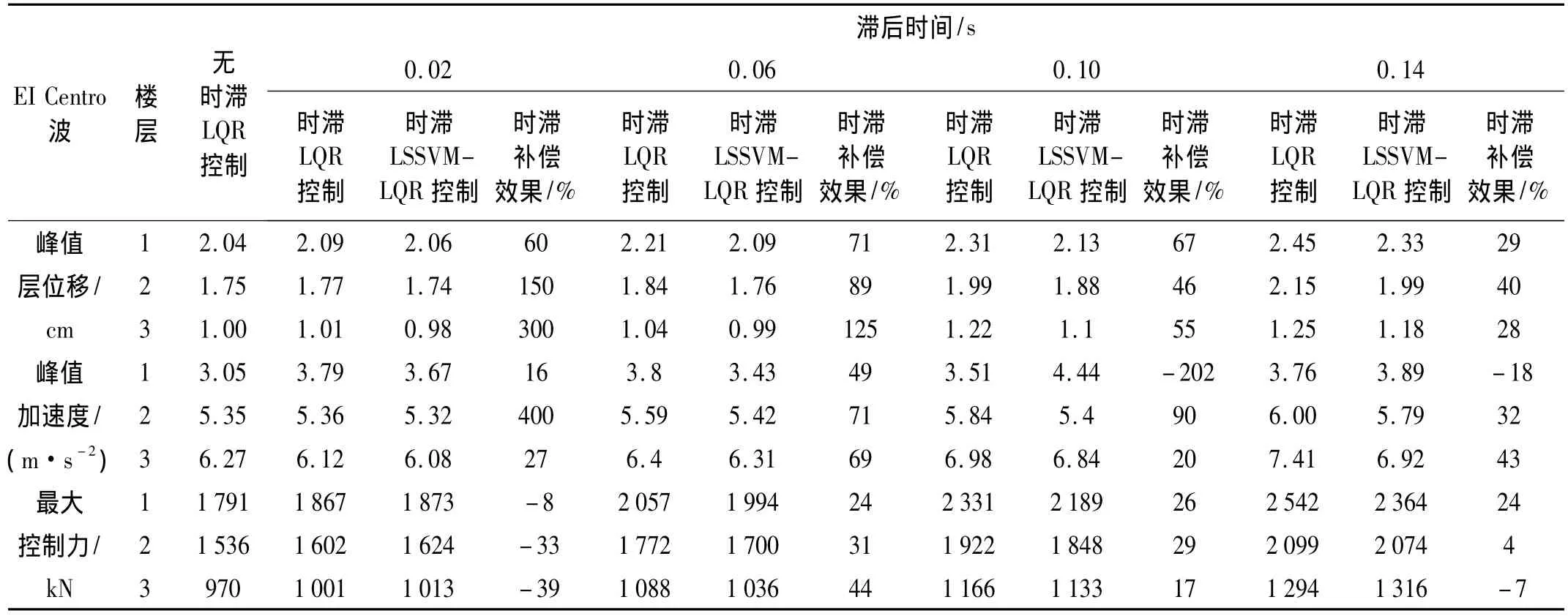
表2 El Centro波作用下结构控制比较Tab.2 Comparison of structural control under the El Centro wave

表3 Loma Prieta波作用下结构控制比较Tab.3 Comparison of structural control under the Loma Prieta wave

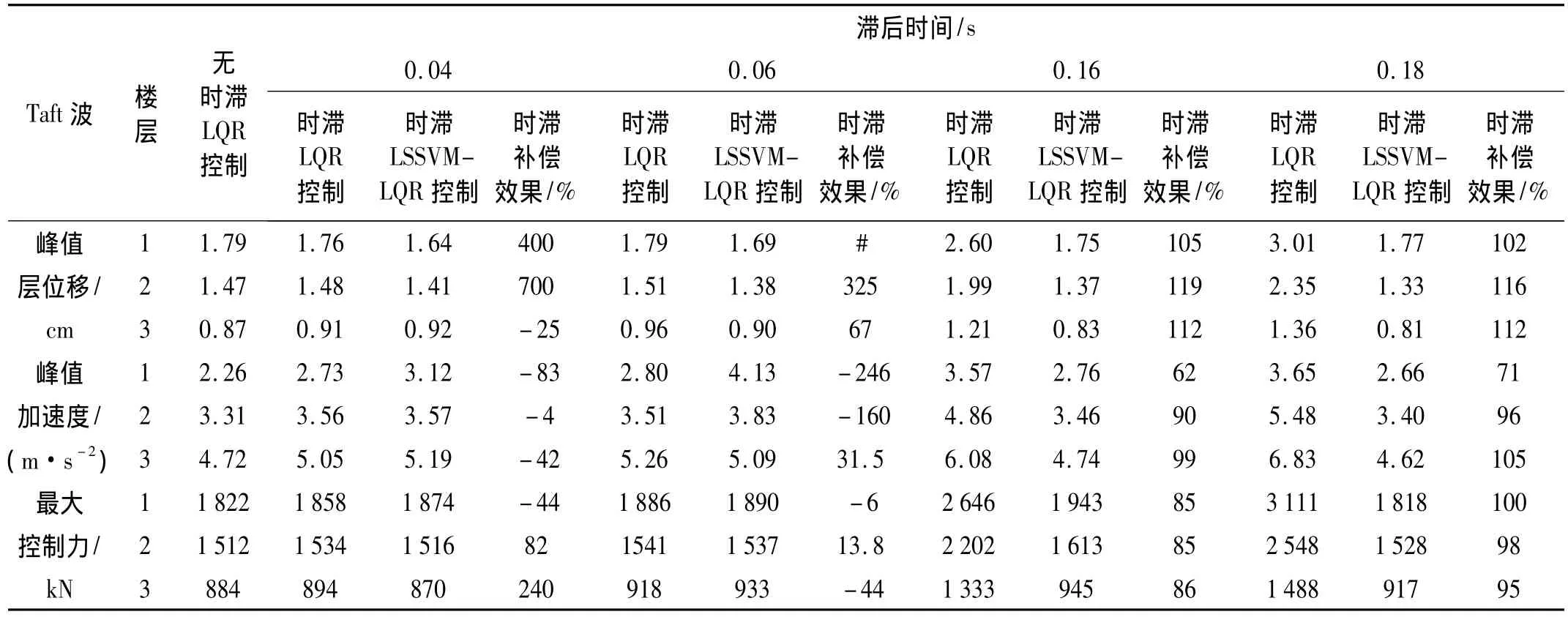
表4 Taft波作用下结构控制比较Tab.4 Comparison of structural control under the Taft wave

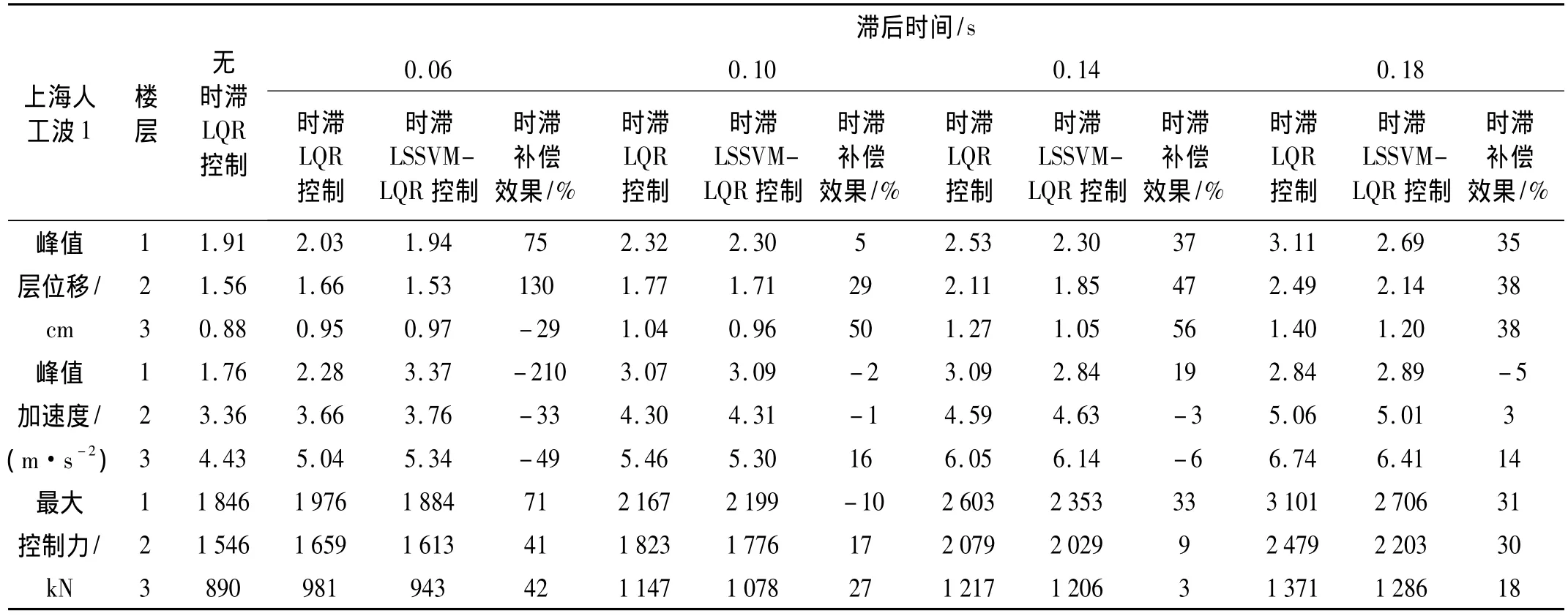
表5 上海人工波1作用下结构控制比较Tab.5 Comparison of structural control under the Shanghai artificial wave 1

图6 四种地震波作用下时滞一定时三种控制算法下结构的峰值位移Fig.6 Peak displacements of the structure with three control algorithms with given time-delay under four kinds of waves

图7 四种地震波作用下时滞一定时三种控制算法下结构的峰值加速度Fig.7 Peak accelerations of the structure with three control algorithms with given time-delay under four kinds of waves

图8 四种地震波作用下时滞一定时三种控制算法下结构的最大控制力Fig.8 Maximum control forces of the structure with three control algorithms with given time-delay under four kinds of waves

图9 El Centro波作用下三种控制算法下结构的顶层响应曲线(时滞0.14 s)Fig.9 Displacement of top storey with three control algorithms with time delay under El Centro wave(time-delay:0.14 s)

图10 Loma prieta波作用下三种控制算法下结构的顶层响应曲线(时滞0.18 s)Fig.10 Displacement of top storey with three control algorithms with time delay under Loma prieta wave(time-delay:0.18 s)

图11 Taft波作用下三种控制算法下结构的顶层响应曲线 (时滞0.18 s)Fig.11 Displacement of top storey with three control algorithms with time delay under Taft wave(time-delay:0.18 s)

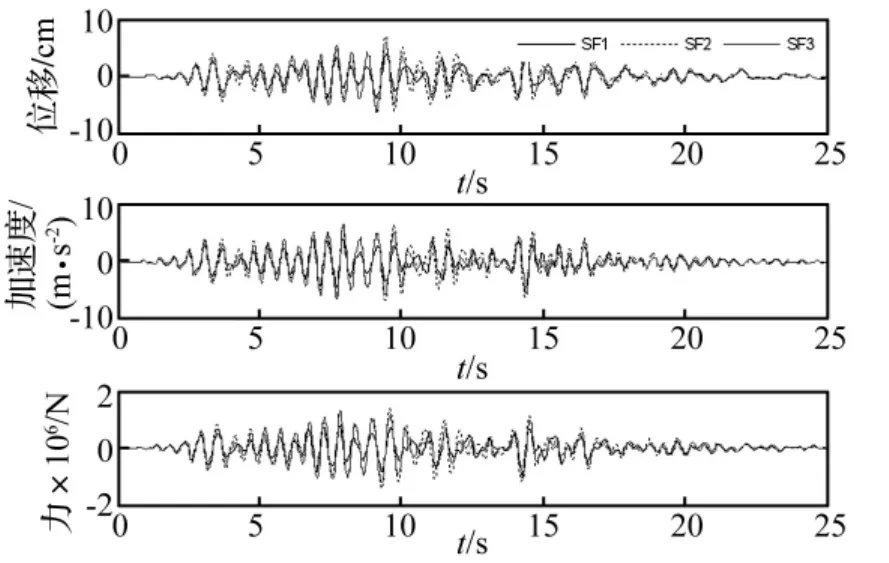
图12 上海人工波1波作用下三种控制算法下结构的顶层响应曲线 (时滞0.18 s)Fig.12 Displacement of top storey with three control algorithms with time delay under Shanghai artificial wave 1(time-delay:0.18 s)

图6～图8为四种地震波作用下时滞一定(时滞最长情况)时三种控制算法下结构的峰值位移、峰值加速度、最大控制力。由图看出，即使时滞较长时，时滞LSSVM-LQR算法的控制效果依然介于无时滞LQR控制与时滞LQR控制效果之间，且其中对Loma Prieta与Taft波的控制效果依然保持较好的控制水平。图9为El Centro波作用下不同控制算法时(时滞0.14 s)结构顶层时程响应曲线;图10为Loma prieta波作用下不同控制算法时(时滞0.18 s)结构顶层时程响应曲线;图11为Taft波作用下不同控制算法时(时滞0.18 s)结构顶层时程响应曲线;图12为上海人工波1作用下不同控制算法时(时滞0.18 s)结构顶层时程响应曲线。由图9～图12知，时滞LQR算法的控制效果较无时滞LQR算法差很多，而时滞LSSVM-LQR算法控制效果较无时滞LQR控制效果稍差些，但较时滞LQR算法控制效果好很多，尤其在极值点附近，效果更明显。只有离极值点较远的极少点的控制效果较时滞LQR控制效果差。值得注意的是，LSSVM-LQR使结构响应趋于平坦的效果有利于抗震。时滞较长时，由于LSSVM回归预测点离最近观测点时间间隔太长，LSSVM预测的最优控制力与实际数据误差较大，LSSVM-LQR的控制效果变得不理想，严重时也会导致响应发散。

5 结论

本文通过建立结构时滞LSSVM-LQR地震响应智能控制算法，基于 MATLAB平台，编制时滞 LSSVMLQR算法的执行程序;用3层框架结构进行数值验证与比较。结论如下:

(1)时滞对结构控制效果与稳定性具有极不利影响，对不同地震波敏感程度亦不相同，其敏感度与地震加速度正反变换速率相关。

(2)时滞LSSVM-LQR可有效减小时滞对结构控制效果影响，但控制效果随时滞的过度加长而变差。

(3)在时滞LSSVM-LQR中，径向基核函数参数的选取对结构地震响应控制效果有很大影响。

［1］欧进萍.结构振动控制-主动、半主动和智能控制［M］.北京:科学出版社，2003.

［2］Lin C C，Chang C C，Chen H L.Optimal H∞output feedback control systems with time delay［J］.Journal of Engineering Mechanics，2006，132(10):1096-1105.

［3］蔡国平，黄金枝.控制存在时滞的线性系统主动控制的滑移模态方法［J］.力学季刊，2002，23(2):164-172.

CAI Guo-ping，HUANG Jin-zhi.Sliding-mode control method for linear systems with time-delay in control［J］.Chinese Quarterly of Mechanics，2002，23(2):164-172.

［4］陈龙祥，蔡国平.地震作用下建筑结构的多时滞最优控制［J］.振动与冲击，2008，27(4):63-65，169.

CHEN Long-xiang，CAI Guo-ping.Optimal control method for scimically excited structures with multiple time delays in control［J］.Journal of Vibration and Shock，2008，27(4):63-65，169.

［5］刘军龙，代晶辉，张春巍，等.基于位移反馈控制的主动增加时滞补偿方法及其试验验证［J］.振动与冲击，2011，30(6):185-191.

LIU Jun-long，DAI Jing-hui，ZHANG Chun-wei，et al.Time delay compensation method based on displacement feedback and active increasing of time delays and its experimental verification［J］.Journal of Vibration and Shock，2011，30(6):185-191.

［6］ McGreevy S，Soong T T，Reinhorn A M.An experimental study of time delay compensation in active structural control［C］.Proc.6th Int.Modal Analysis Conf.and Exhibits，Society for Experimental Mechanics，1988:1733-1739.

［7］徐龙河，李忠献，钱稼茹.半主动预测控制系统的时滞与补偿［J］.工程力学，2011，28(9):79-83.

XU Long-he，LI Zhong-xian，QIAN Jia-ru.Time delay and compensation for semi-active predictive control system［J］.Engineering Mechanics，2011，28(9):79-83.

［8］Vapnik V.Statistical learning theory［M］.New York:Wiley，1998.

［9］ Cheng J S，Yu D J，Yang Y.Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform［J］.Mechanical Systems and Signal Processing，2007，21(3):1197-1211.

［10］ David M，Bart B，Tony V G.Comprehensible credit scoring models using rule extraction from support vector machines［J］.European Journal of Operational Research，2007，183(3):1466-1476.

［11］ Suykens J A K，Vandewalle J.Least squares support vector machine classifiers［J］.Neural Processing Letters，1999，9:293-300.

［12］顾燕萍，赵文杰，吴占松.最小二乘支持向量机的算法研究［J］.清华大学学报(自然科学版)，2010，50(7):1063-1066，1071.

GU Yan-ping， ZHAO Wen-jie， WU Zhan-song. Least squares support vector machine algorithm［J］.J Tsinghua Univ(Sci＆Tech)，2010，50(7):1063-1066，1071.