层状周期结构动力衰减域特性研究

程志宝，石志飞，向宏军

(北京交通大学 土木建筑工程学院，北京 100044)

作为复合材料/结构(简称周期性材料或周期性结构)的声子晶体材料/结构因其具有周期排列特性而广受关注［1-3］。其存在的频率禁带(衰减域)及通带(非衰减域)特性滤波性质，可为各种滤波器研制、工程结构隔震/减振降噪材料设计与开发提供新途径［4］。

在土木工程领域，各种形式动力作用直接影响建筑物的安全性与舒适性。尤其地震给人类生命财产的安全带来极大威胁［5］。为减弱地震对建筑结构造成的损害，出现了各种形式的结构减、隔震技术。其中基础隔震为实践证明且较有效的抗震措施［6］。石志飞等［7-9］将固体物理学中有关周期性结构特性引入土木工程领域，提出的研制周期性隔震基础设想及有益探索表明，利用周期性基础进行基础隔震可行。

本文通过推导层状周期结构色散方程，建立衰减域边界控制方程并给出物理解释;分析层状周期结构带隙的产生条件，研究各种因素对衰减域三个控制参数(衰减域起始频率、衰减域宽度、衰减因子)影响。用有限元软件，数值研究有限层状周期结构的谐响应及瞬态响应，并制作隔震试件完成振动台实验，进一步证实层状周期结构的动力衰减特性。该研究可为将层状周期结构应用于工程结构隔震、减振提供基础。

1 基本理论－色散带隙及衰减因子

两种均匀材料组成的一维层状周期结构见图1(a)。设结构沿x-y平面内无限大，沿z方向无限周期性交替排布，两种材料界面完全粘结。取x-z平面内沿z方向传播的剪切波Sx进行研究，分析周期性结构中波的色散特性。利用周期性理论，取其中一个单元见图1(b)。

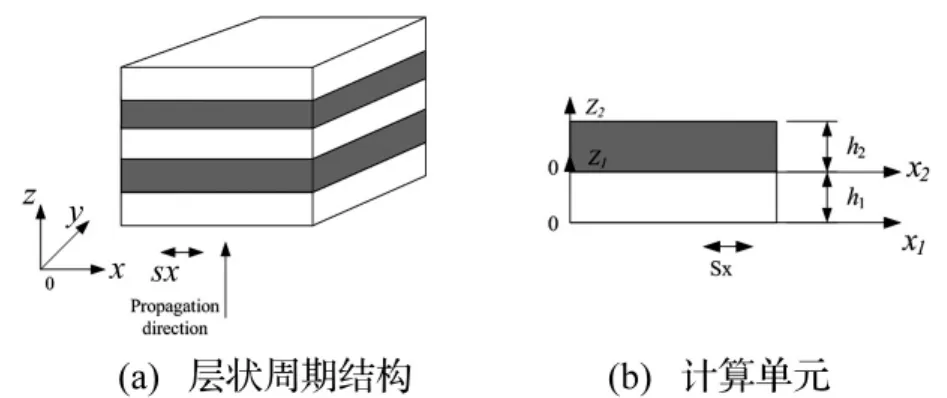
图1 层状周期结构及计算单元示意图Fig.1 Configuration of layer periodic structure and the Wigner-Seitz cell

设u为质点沿x的振动位移，ρ为材料密度;λ和μ为材料的拉梅常数。剪切波Sx的控制方程为:

应用傅里叶变换，两种材料在局部坐标系下分别求解式(1)，可得其位移与剪应力稳态解:

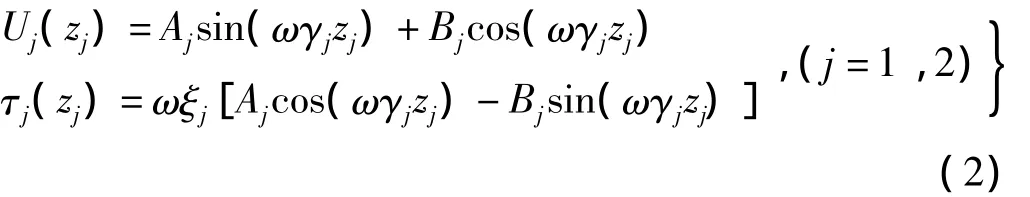
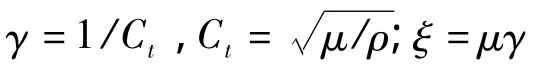
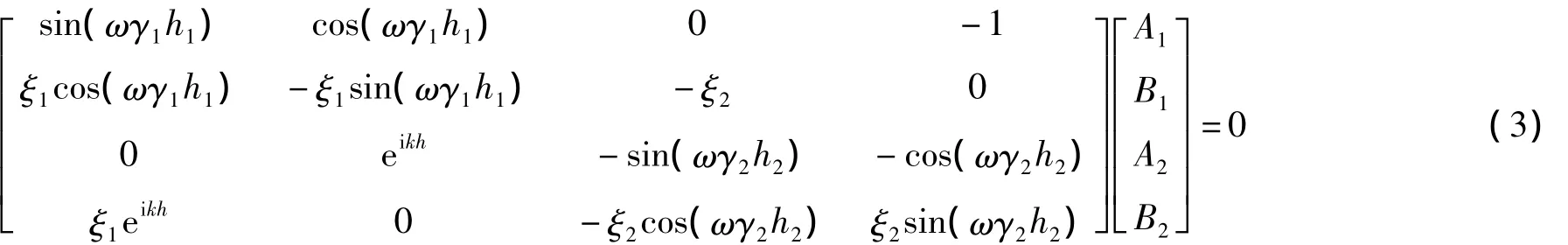
其中:k=α+iβ为复数波矢，α为相位因子，β为衰减因子［12］。式(3)的系数矩阵行列式等于零，由此可得色散曲线解析表达式为:

采用工程中常用的混凝土与橡胶材料构造层状周期结构，材料常数见表1。混凝土层与橡胶层厚度均取0.2 m。周期结构的色散曲线见图2。在0～35 Hz范围内存在两个完整带隙6.565～15.005 Hz与17.81～30.10 Hz。由于工程结构多为0～50 Hz的低频振动，因此上述带隙可用于工程结构的隔震、减振。

本文算例的衰减因子随频率变化关系见图3。在禁带范围内，衰减因子关于带隙中心频率大致对称，第一滤波带中心衰减因子为3.54，带隙边界对应的衰减因子为零。

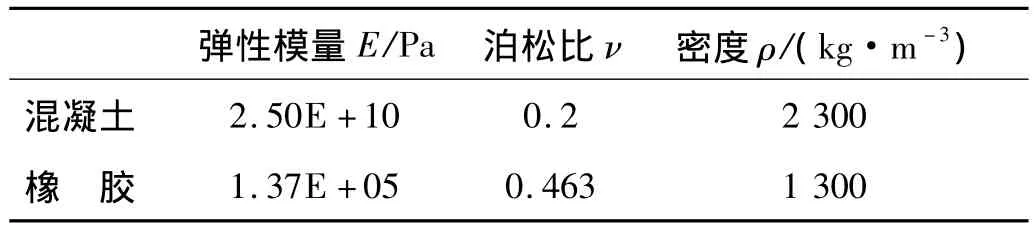
表1 材料参数Tab.1 Material coefficients

2 层状周期结构衰减域参数控制

工程结构振动具有低频宽带特性，周期结构衰减域(禁带)应起始频率低、衰减域宽。尤其第一衰减域，起始频率越低且衰减域越宽，对结构隔震、减振越有利。衰减域应彻底滤掉某些频率范围的波，故希望衰减因子尽可能大。第一衰减域起始频率(FLBF)、衰减域宽度(FWAZ)及衰减域衰减因子(β)构成衰减域三个控制参数。以下分别讨论周期结构的物理参数及几何参数对第一衰减域控制参数的影响。

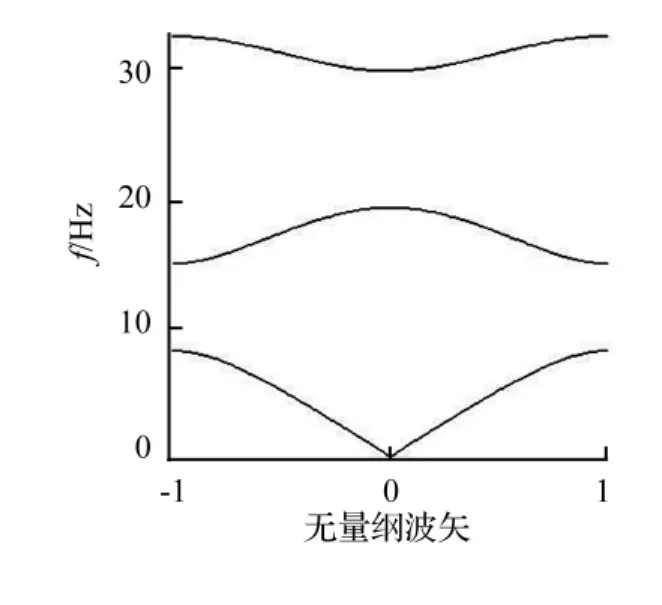
图2 色散曲线Fig.2 Dispersion curves

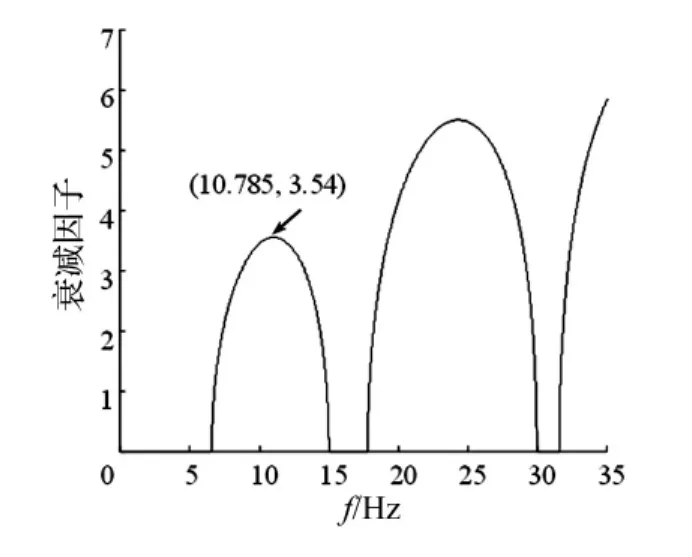
图3 衰减因子Fig.3 Attenuation parameters

图4 混凝土层厚度对第一衰减域的影响Fig.4 Effects of the thickness of the concrete layer on the first AZ

2.1 第一衰减域起始频率及宽度

欲获得较低的第一衰减域起始频率，即使色散曲线初始斜率尽可能小。将原点处切线方程ω=Ck代入式(4)，并化简得:

式(5)对h1或h2求导得:

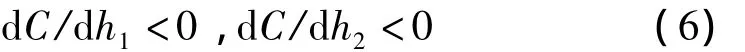
可见，当材料的物理属性不变时，随着单元组分材料厚度增大，原点处相速度减小，即第一衰减域的起始频率降低。混凝土层厚度变化时，FLBF与FWAZ的变化趋势见图4。FLBF随混凝土层厚度的增加而减小，但FWAZ随着混凝土层厚度的增加会增加。

对物理因素ζ与γ，两者耦合于材料中。ζ为两种材料波阻抗差异，ζ=μγ为某一材料的波阻抗。将ζ与γ视为两独立参数进行分析:

例如，必修2有关艾弗里证明DNA是遗传物质的实验中，教材所展示的是分别将分离的蛋白质、多糖、DNA等加入R型菌的方法（做加法），而新版教材将改变为更接近艾弗里真实实验的逐步排除的方法（做减法）。教师应当补充这些内容给学生。

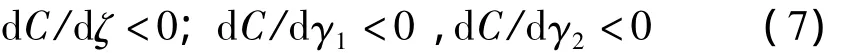
随ζ的增大，原点处相速度减小。FLBF与FWAZ随ζ的变化见图5。FLBF随ζ的增加而减小;FWAZ随ζ的增加而增加。随剪切波速的减小，γ增大，原点处斜率减小，第一衰减域起始频率降低。FLBF与宽度FWAZ随橡胶层材料的剪切波速单独变化关系见图6。可看出，随橡胶材料剪切波速的增加，FWAZ增加急剧;而FLBF则增加缓慢。

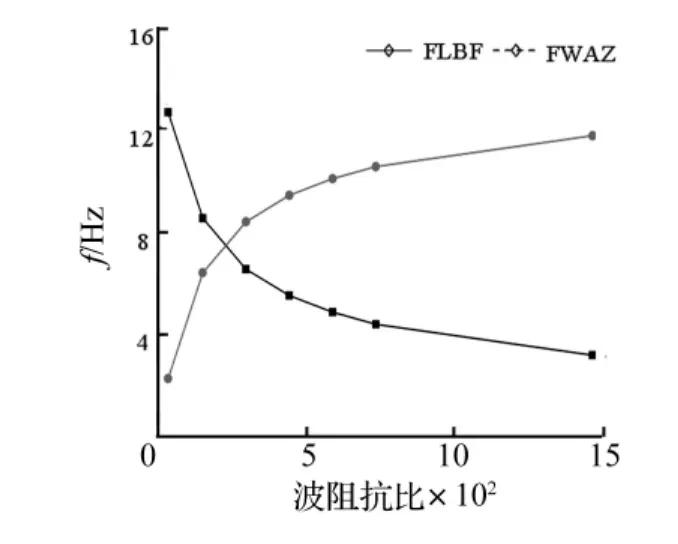
图5 第一衰减域随材料波阻抗差系数的变化Fig.5 Effects of the wave impedance coefficient on the first AZ

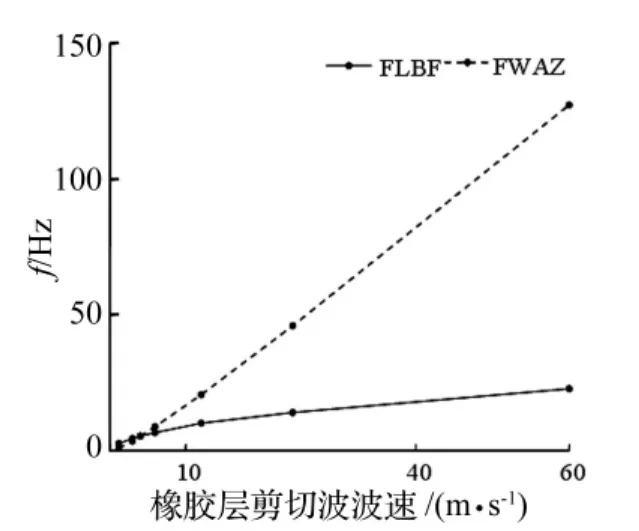
图6 第一衰减域随橡胶材料剪切波波速的变化Fig.6 Effects of the shear wave velocities of the rubber layer on the first AZ

图7 几何参数对最大衰减因子的影响Fig.7 Effects of geometrical parameters on the max attenuation parameter

2.2 第一衰减域衰减因子

衰减域的衰减特性由衰减因子控制。利用周期性结构阻隔波动传播时，通常希望某些频段波通过衰减域时能被充分过滤，即希望有大的衰减因子。为此，分析各种物理参数及几何参数对衰减因子影响。材料厚度及波阻抗比对最大衰减因子影响见图7。由图7看出，其它物理参数不变时，随混凝土层厚度增大，衰减因子总在减小;随橡胶层厚度增大，衰减因子先增大后减小，变化幅度不大。衰减因子随材料波阻抗差系数的增大而增大。

3 数值模拟与实验验证

将无限周期结构频率带隙特性应用于工程结构隔震、减振，需研究有限周期结构动力特性。应用Ansys有限元分析软件，对有限层状周期结构进行分析。采用Soild-45实体单元建模，平面尺寸为8 m×8 m。同时通过实际地震动实验，证明层状周期结构对地震动具有的良好阻隔效果。

3.1 谐响应分析

有限层状周期结构，周期数取9，混凝土层与橡胶层厚度取0.2 m。约束模型底部y，z方向位移，沿x方向施加幅值为1、频率0～35 Hz以内的简谐位移荷载，频率间隔0.1 Hz，计算不同频率下有限周期结构动力稳态响应。

经2、4个周期单元滤波后的位移响应函数见图8。由图看出，有限周期结构存在明显的衰减域，两个衰减域分别与第一带隙及第二带隙对应。ω=10.785 Hz时层状周期结构的瞬态解与稳态解比较见图9。其中，瞬态解为周期结构底部输入单一频率正弦激励且t∈［0，5 s］时，周期结构各层响应幅值。由图9看出，有限周期结构中振动幅值沿z轴变化的数值解与无限周期结构中振动幅值沿z轴变化的理论解完全吻合。在不计入瞬态效应情况下，衰减域中的振动主要集中在前1～2个周期范围内，经2个周期后振动幅值减小到5%左右;计入瞬态效应后衰减幅度略有减小，在顶层自由边界处存在鞭梢放大效应，但经3个周期后振动仍可衰减到20%左右，鞭梢效应影响并不大。

3.2 组合频率时程分析

由于衰减域内振动传播主要集中在前2～3个周期内，瞬态效应及自由边界影响有限。为此分析含4个周期数的层状结构在组合频率下第一衰减域内结构反应。设归一化组合频率位移时程为:

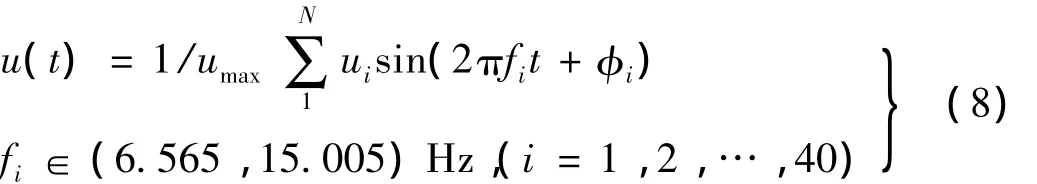
其中:ui为(0，1)之间单频率幅值随机数，φi为(0.2π)之间相位随机数，umax为组合位移时程最大值。约束底部y、z方向位移而沿x方向输入组合位移时程，时间步长Δt=0.005 s。0～5 s内顶层位移响应见图10。可以看出，外部激励经四个周期传播后，减小80%以上。

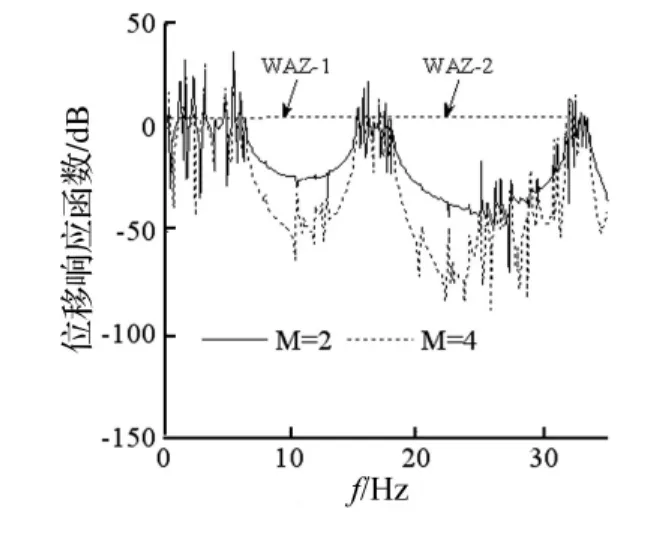
图8 位移响应函数Fig.8 Displacement response function

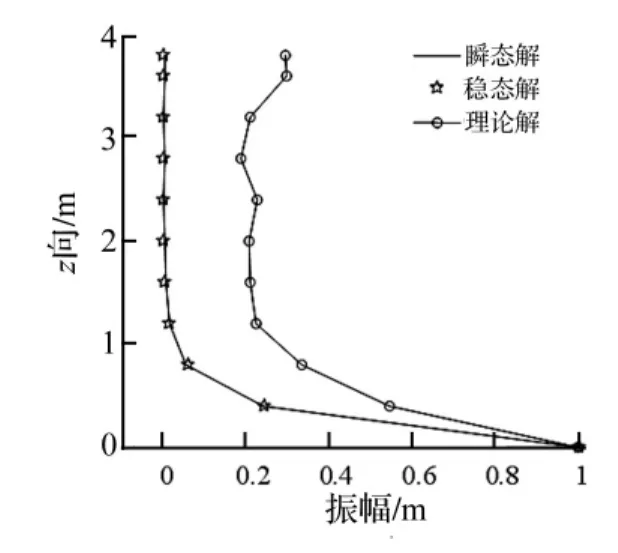
图9 瞬态与稳态衰减对比Fig.9 Attenuation comparison

图10 组合频率位移时程对比Fig.10 Comparison of the displacement response

图11 振动台实验Fig.11 Shaking table test

3.3 实验验证及数值分析

为进一步探明层状周期结构基础减振、隔震特性，进行两方面实验:① 频域测试，了解结构在不同激励频率下的响应特性;② 输入真实地震动，测试其中包含的多种频率成份，观察地震动主频段落在衰减域内时周期基础的隔震滤波效果。本试验取后者。

实验在台湾地震研究中心完成。实验中制作的两缩尺三层钢框架结构完全相同，其一直接固定在振动台上，另一个固定在周期性基础上，见图11。钢框架柱0.06 m ×0.06 m;梁截面 0.03 m ×0.06 m;梁、柱截面钢板厚0.0032 m。楼板厚0.003 m。框架平面0.6 m×0.6 m，层高0.3 m。每层配重20 kg。周期性基础含三层混凝土及两层橡胶，层厚均0.2 m，平面1.0 m×1.0 m。

由于模型在平面内对称，实验时振动台仅在水平向一个方向输入1975 Oroville地震加速度记录［13］。该地震加速度记录的傅里叶谱见图12，从图中看出地震动主频段处于衰减域范围内。有无隔震基础情况下上部结构顶层水平加速度响应实验结果见图13。从图中可见有层状周期基础情况，上部结构加速度响应减小近50%。本文实验模型，应用ANSYS进行数值模拟，结构阻尼比取5%。有周期基础情况的上部结构顶层加速度响应数值模拟结果与实验测试结果见图14，由图可见两者符合较好。因此，工程中利用周期性结构具有的衰减域特性进行隔震、减振可行。

图12 地震加速度记录的傅里叶谱Fig.12 Fourier spectrum of the earthquake acceleration record

图13 顶层加速度响应Fig.13 Acceleration response at top floor

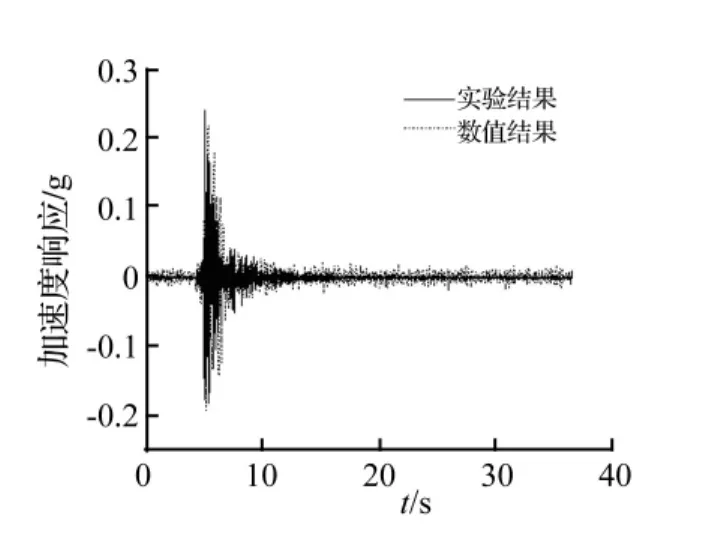
图14 结果对比Fig.14 Results comparisons

4 结论

本文给出层状周期结构衰减域边界控制方程，并分析影响衰减域的三个特性参数，对层状周期结构动力衰减域特性进行数值模拟与实验验证。结论如下:

(1)材料物理属性不变时，第一衰减域起始频率(FLBF)与宽度(FWAZ)随混凝土层厚度的增加而减小;FLBF随橡胶层厚度的增加而减小，但FWAZ随橡胶层厚度的增加而增加，有利于工程应用。

(2)剪切波速一定情况下，随材料波阻抗差别的增大FLBF会减小，而FWAZ与衰减因子会增大。随材料剪切波速的增加，FWAZ增加;FLBF随橡胶层材料剪切波速的增加而缓慢增加。工程中应据具体衰减域要求确定层状结构的各种参数。

(3)频率在衰减域范围内的外部激励，在层状周期性结构中传播主要集中在前1～2个周期。经2个周期后振动可衰减到5%左右，计入瞬态效应后，响应衰减有所降低，但仍达80%以上。

(4)弹性波或振动在层状周期结构中传播类似于半波反射，层状周期基础可有效降低地震动作用下上部结构响应，周期结构在工程结构的隔震、减振中具有广阔的应用前景。

［1］ Kushwaha M S，Halevi P，Dobrzynski L，et al.Acoustic band structure of periodic elastic composites［J］.Physical Review Letters，1993，71(13):2022-2025.

［2］Liu Z Y，Zhang X X，Mao Y，et al.Locally resonant sonic materials［J］.Science，2000，289:1734-1736.

［3］温熙森.声子晶体［M］.北京:国防工业出版社，2009.

［4］ Xiang H J，Shi Z F.Analysis of flexural vibration band gaps in periodic beams using differential quadrature method［J］.Computers and Structures，2009，87(23-24):1559-1566.

［5］ Ye L P，Lu X Z，Qu Z，et al.Analysis on building seismic damage in the Wenchuan earthquake［C］.The 14thWorld Conference on Earthquake Engineering， Beijing，China，2008.

［6］李宏男，霍林生.结构多维减震控制［M］.北京:科学出版社，2008.

［7］Jia G F，Shi Z F.A new seismic isolation method and its feasibility study［J］. Earthquake Engineering and Engineering Vibration，2010，9(1):75-82.

［8］ Xiang H J，Shi Z F，Bao J.Seismic isolation of buildings with a new type of periodic foundations［C］.ASCE Earth and Space 12th Conference，Honolulu，Hawaii，2010.

［9］ Shi Z F，Cheng Z B，Xiong C.A new seismic isolation method by using a periodic foundation［C］.ASCE Earth and Space 12th Conference，Honolulu，Hawaii，2010.

［10］温激鸿.声子晶体振动带隙及减振特性研究［D］.长沙:国防科技大学，2005.

［11］ Delph T J，Herrmann G，Kaul R K.Harmonic wave propagation in a periodically layered，infinite elastic body:antiplane strain［J］.Journal of Applied Mechanics，1978，45(2):343.

［12］ Mead D J.Wave propagation in continuous periodic structures:Research contributions from Southampton［J］.Journal of Sound and Vibration，1996，190(3):495-524.

［13］ Peer.Peergroud motion database ［C］. http://peer.berkeley.edu/peer_ground_motion_database，2011.