基于音圈电机X-Y精密定位平台的控制系统设计*

冷同同，靳 东，刘博峰

(1.山东大学机械工程学院，济南 250061;2.上海交通大学 机械与动力工程学院，上海 200240)

0 引言

随着超精密智能器件和执行机构的广泛应用，以及高性能数字系统的快速发展，超精密机电伺服系统已逐步应用到许多新兴行业，例如，芯片封装［1］、半导体加工［2］等。为满足人们对这类精密机电系统在准确性、稳定性、快速响应以及鲁棒性等方面的苛刻要求［3-4］，精密控制算法成为解决这类问题的关键技术。尤其是，精密定位控制越来越多的被研究讨论［5］。

由于高速、高精度运动控制的限制，许多控制方法在精密定位控制中难以应用，这使得精密定位控制算法存在一定的挑战。例如，由于环境干扰、机械摩擦［6］以及不能完全准确的建立系统数学模型而造成的模型不确定等问题的影响［7］，传统PID控制并不是总能保证系统具有良好的性能。鲁棒控制理论的出现，成为解决上述问题的关键基础。文献［8］针对XY伺服平台系统提出了零相位的鲁棒控制方法。本文针对由音圈电机驱动的X-Y精密定位平台，进行系统辨识，建立系统的数学模型。在系统数学模型的基础上，采用混合灵敏度优化的方法，设计一种H∞鲁棒控制器，能够较好的抑制外部干扰和不确定性对系统造成的影响，从而使被控系统获得更好的性能。

1 X-Y精密定位平台

1.1 X-Y精密定位平台介绍

如图1所示，为音圈电机驱动的X-Y精密定位平台。该平台主要由X、Y上下两个方向的平台，两个100nm精度的直线光栅(用于反馈位置信号的位移传感器)，以及三个音圈电机组成。该音圈电机为移动线圈式(NCC)，其外圈固定部分是永磁体，内圈直线运动部分为线圈(图1中的红色部分)。另外，所需的电流由Quanser公司的线性功率放大器提供。目前，线性功率放大器已用于多个领域，例如，仪器仪表行业、纳米技术、光学加工等。

图1 X-Y精密定位平台结构图

1.2 x方向的系统建模及辨识

1.2.1 系统建模

考虑到定位平台的结构特点及实际工作情况，我们将x方向系统的机械模型简化为弹簧阻尼系统，如图2所示。

图2 X-Y精密定位平台x方向的动力学模型

其中，Mx为x方向的等效运动质量，Cx为x方向的等效阻尼系数;Kx为x方向的等效刚度;Fx为音圈电机产生的驱动力。

根据牛顿第二定律，可以得到x方向系统的动力学方程：

式中，Fx=KFIx，KF为音圈电机的力常数，Ix为提供给音圈电机的电流。由于线性功率放大器具有的高带宽特性(带宽500Hz左右)，因此，可以将放大器的动力学特性近似为一个直流增益，即：

因此，控制电压到位置的传递函数表达式为：

由上式可知，该X-Y精密伺服定位系统的数学模型为一个二阶模型。

1.2.2 系统频域辨识

在频域分析中，傅里叶变换是重要的数学手段之一，其中离散傅里叶变换因适合数字系统的分析与处理，在工业领域得到广泛的应用。

为了获得具体的系统传递函数，我们采用一种以S函数为基础的实时在线DFT算法来进行系统辨识，以正弦扫频电压信号输入给线性功率放大器，作为系统的激励信号(如图3所示)。S函数(System-Functions)可以通过 Matlab、C、C++或 Fortran等编写成功，能够不停的更新系统状态，适用于离散、连续或者混合系统。最重要的是，结合Simulink Coder产品可以从S函数自动生成可执行代码，缩短开发周期。

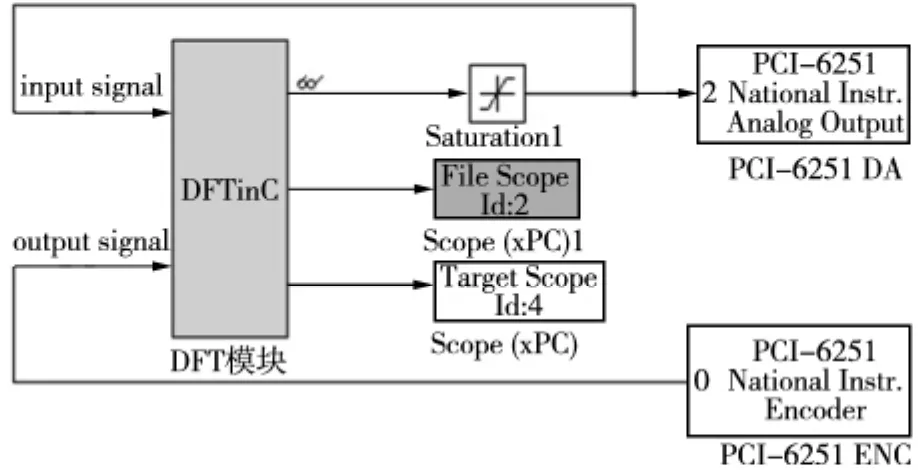
图3 实时在线DFT算法实验

如图4所示，S函数在运行过程中通过一系列的回调函数来执行任务。该算法中主要用到的回调函数［9］为：

(1)mdlInitializeSizes用来指定S函数的输入、输出、状态、参数等的数量;

(2)mdlInitializeSampleTimes用来指定S函数工作时的采样频率;

(3)mdlStart用以初始化S函数的变量值;

(4)mdlOutputs计算S函数的输出值;

(5)mdlUpdate更新S函数的状态、参数等;

(6)mdlTerminate执行仿真结束时需要进行的相关操作。

图4 S函数模块运行流程图

另外，上述扫频程序的S函数模块(DFT模块)需满足以下要求：

(1)正弦扫频信号在各个频率上应整周期进行，因此应根据实际情况对采样点数(N)进行设定;

首先，对各个频率的采样点数进行赋值，以n表示，再根据以下程序，调整n，获取实验所用采用点数N，从而使正弦信号在各个频率上整周期进行。

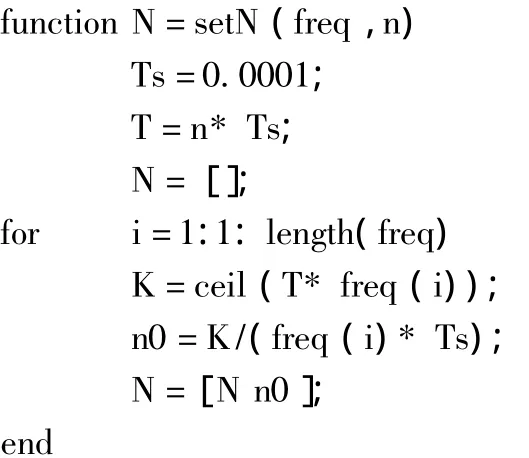
(2)同时对两个输入到DFT模块的信号(input signal和output signal)进行DFT运算，从而求得输入、输出信号的幅值比和相位差。

综合考虑机械系统及硬件上的可行性，将实验的采样频率设为10K，相应的奈奎斯特频率为5K。

所需实验数据(图3所示File Scope 2中的数据)可直接通过TCP/IP网络协议，由目标机传递到主机上。得到的结果为原始输入、输出信号在相应频率下实部与虚部的值，根据：

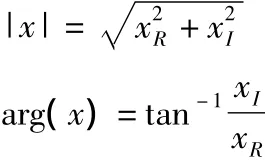
即可得到输入、输出信号相应的幅值和相角。因此，系统频率响应即为：

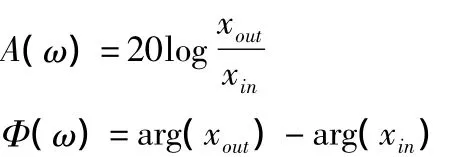
分析上述幅值和相角的数据，即可得到如图5所示的开环频率响应曲线(蓝色曲线)。通过Levi数据拟合的方法，最终得到拟合后的频率特性响应曲线(图示红色曲线)，以及拟合的系统传递函数：

图5 开环频率特性曲线

注：进行扫频实验时，往往需要较长的频率序列及多次实验，这样势必会带来较大的数据处理量。与离线DFT变换相比，实时在线DFT算法显著降低了数据I/O量及处理量，提高了效率。

2 控制器设计

2.1 混合灵敏度优化

混合灵敏度优化方法是鲁棒控制理论中的典型方法之一，它能够将对系统鲁棒稳定和鲁棒性能的要求转化为H∞范数优化问题，并能有效地抑制模型不确定及外部干扰对系统性能的影响［10］。

如图6所示，为混合灵敏度优化的控制结构图。r为参考输入，u为控制输出，G(s)为被控对象的数学模型，C(s)为控制器，W1(s)为性能权函数，W2(s)为鲁棒权函数。

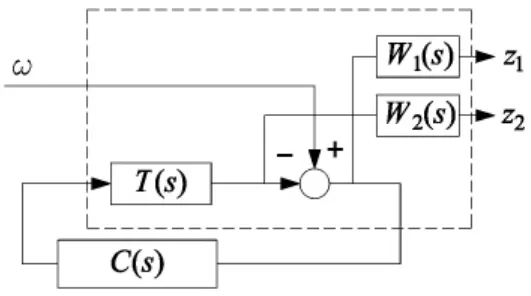
图6 混合灵敏度控制结构图

定义灵敏度函数S(s)及补灵敏度函数T(s)为：

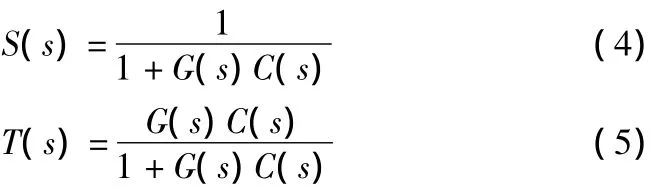
即，寻找控制器K(s)，使得闭环系统稳定，且使得H∞范数最小，从而获得最优的性能指标γopt及相应的H∞控制器Kopt，如下所示：

2.2 权函数的选择

性能权函数W1(s)一般选择为具有积分特性或高增益低通特性，从而满足系统能有效抑制干扰的要求。因此，定义W1(s)为如下形式：

则我们的设计目标为：

而鲁棒权函数W2(s)则可根据系统的未建模动态来选取。考虑如下具有未建模动态的不确定系统：G'(s)=G(s)+ΔG(s)=G(s)(1+Δ(s))，W2(s)应满足：

结合X-Y精密定位平台的数学模型，选取：

3 仿真及实验验证

3.1 仿真结果

基于X-Y精密定位平台的系统传递函数，根据第二单元所述权函数的选用原则。分别选取权函数：

利用公式(6)从而获得一个6阶的H∞鲁棒控制器，如图7所示。

仿真结果(图8所示)表明，该控制器调整时间在0.01s以内，系统具有响应速度快，无超调，稳态时无静差等优点。与PID控制器相比，明显改善了系统的动态性能。

另外，文献［5］中的阶跃响应调整时间小于0.02s，无超调。可以看出，本文的响应时间更短，速度更快。

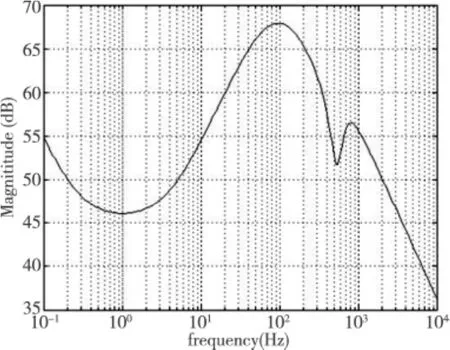
图7 H∞鲁棒控制器

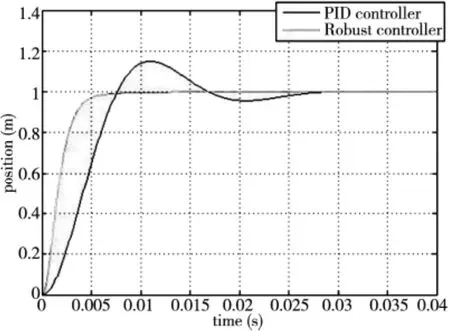
图8 仿真条件下的系统阶跃响应图

3.2 实时控制实验结果

基于xPCTarget及National Instruments(NI)公司的PCI6251数据采集卡的实时控制系统，在图1所示的X-Y精密定位平台上实现了该H∞鲁棒控制器，从而验证了该控制算法的有效性。实时控制实验结果(图9所示)与仿真结果基本一致，表明该控制器用于实际系统中，同样会改善系统的性能。

图9 实验条件下的系统阶跃响应图

4 结论

基于音圈电机驱动的精密伺服平台越来越受到人们关注。针对X-Y精密定位平台，提出了一种实时DFT算法，得到系统的开环频率响应，进而获取系统的数学模型。为抑制模型不确定及外部干扰对系统造成的影响，采用混合灵敏度优化的方法来设计H∞鲁棒控制器。最终的仿真及实验结果(调整时间在0.01s以内且无超调)表明，该控制器使得精密机电系统的响应速度更加快速、稳定性更强。

［1］S.L.Chen，T.H.Hsieh.Repetitive control design and implementation for linear motor machine［J］.International Journal of Machine Tools and Manufacture，2007，47(12)：1807－1816.

［2］S.Verma，W.J.Kim，H.Shakir.Multi-axis maglev nanopositioner for precision manufacturing and manipulation applications［J］.IEEE Transactions on Industrial Applications，2005，41：1159 －1167.

［3］张金龙，刘阳.纳米级超精密定位工作台的研究［J］.机械工程学报，2011，47(9)：187 －192.

［4］张大卫，冯晓梅.音圈电机的技术原理［J］.中北大学学报，2006，27(3)：224 －228.

［5］张大卫，杜伟涛，冯晓梅.面向芯片封装的高速精密定位平台控制系统设计［J］.天津大学学报，2006，39(9)：1060－1065.

［6］H.Shinno，H.Yoshioka，K.Taniguchi.A newly developed linear motor-driven aerostatic X-Y planar motion table system for nano-machining［J］.CIRP Annals-Manufacturing Technology，2007，56(1)：369 －372.

［7］申铁龙.H∞控制理论及应用［M］.北京：清华大学出版社，1996.

［8］赵希梅，孙显峰，高君.XY平台伺服系统的零相位鲁棒控制［J］.组合机床与自动化加工技术，2012(7)：68－70.

［9］曹戈.MATLAB教程及实训［M］.北京：机械工业出版社，2008.

［10］孙宜标，王通，孙晓雨.复合AC轴直接驱动伺服系统混合灵敏度速度控制［J］.组合机床与自动化加工技术，2010(3)：38－42.