基于OD与LHS的复杂作用关系制造过程的计算机实验方法*
2013-09-12崔庆安
崔庆安
(郑州大学管理工程学院,郑州 450001)
0 引言
对于产品实现复杂且成本较高的自动化加工制造过程,计算机仿真是实现产品优化设计的主要手段之一。其基本原理是根据物理或化学的先验知识,建立实际制造过程的数学模型,而后利用有限元分析等数值计算方法,通过运行计算机程序代码对制造过程进行仿真模拟[1]。由于计算机仿真模型的计算复杂度高,计算时间长,为提高优化设计的效率,研究者引入了计算机实验(Computer experiments,CE)的方法[2]。即采用实验设计(Design of Experiments,DOE)的方法[3],对计算机仿真过程的输入输出进行采样,拟合出该过程的统计学代理模型,并通过对代理模型的寻优来实现优化设计。计算机实验已被广泛地应用于汽车制造、机械电子加工、生物医药合成、航空航天设计等领域[4-5],取得了显著的成效。
如何得到预测性能较好的统计代理模型,是计算机实验的关键问题。为提高模型对于复杂过程的全局性描述能力,多采用 Kriging[6]、ANN[7]、SVR[8]、B-样条函数等结构较为灵活的非参数模型作为基本代理模型,其中应用最广泛的是Kriging模型。此方面的研究较成熟,众多研究者对于代理模型的性能对比、Kriging模型的优势等等进行了深入研究[9-10]。模型形式确定后,实验设计方式的选择就成为关键。目前常用的是以超拉丁方抽样[11](Latin hypercube sampling,LHS)、均匀设计[12](Uniform design,UD)为代表的空间填充设计。LHS与UD的实验点个数与因子个数无关,并且实验点在各因子维度上的投影是均匀和不重叠的,因此可以将少量的实验点均匀地散布在可行域内。但是当因子个数较多时,少量的实验点对于可行域空间的填充程度不够,而且极有可能出现实验点较为稀疏的子区域,极大影响了代理模型的性能。为提高代理模型的全局性预测性能,不得不采用较大的样本量。对于空间填充设计来说,如何实现样本量与模型的全局性预测性能的之间平衡,有价值的研究尚不多见。
事实上,对于计算机仿真过程来说,由于输入因子与输出特性之间存在着复杂的非线性关系,因而输出特性在可行域内的变化是不均匀的,一味地追求实验点的均匀分布,并不一定能够反映这种变化特征。如果能够根据输出特性的变化情况,有针对性地调整空间填充设计实验点的分布,在输出特性变化较大的空间安排较多的实验点,而在输出特性变化较小的空间安排较少的实验点,将会在降低实验设计样本量的同时提高代理模型的预测性能。
本文提出一种基于正交设计和LHS的两阶段实验设计策略,首先以正交设计初步探知输出特性方差在可行域内的变化规律,根据其变化程度,识别出输出特性变化较大的子区域,而后在此子区域内采用LHS来安排实验点,再利用Kriging模型建立起过程的全局性模型。
1 理论简介
1.1 计算机实验的基本原理
设计算机仿真过程的输入因子为x=[x1,…xm]',其可行域为X∈Rm,输出特性为 y,且 y与 x之间存在某种确定型关系,即:

式(1)通常高度复杂,不存在明确的解析表达式,一般采用有限元分析等数值计算的方法来表达。这样一来,当仿真模型的精度较高时,程序运行需要耗费大量时间。例如对于汽车车身结构的优化设计,用于模拟车身正面碰撞过程的有限元模型的单元可达数万,完成一次车身结构的优化需要数百小时。此时,建立计算机仿真过程的统计学代理模型以简化计算就显得十分有必要。即首先选择某种形式的代理模型(例如Kriging模型),而后根据某种准则生成实验设计集

分别以x1,…,xn为输入,运行计算机仿真过程,获取对应的输出特性值y1,…,yn,形成样本集:

再根据该样本集拟合出式(1)的具体统计学代理模型:

由于g(x)一般较为简单,且具有明确的解析表达式,因此用其来近似的代替计算机仿真过程将会显著地缩短计算时间,而且可以通过对g(x)的寻优近似地实现产品的优化设计。为保证优化结果的精度,希望在可行域X内,g(x)对于f(x)的预测误差越小越好,即:
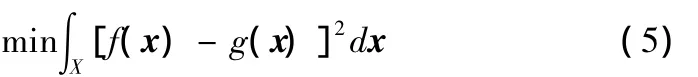
1.2 超拉丁方抽样
与传统的因子设计、中心复合设计相比,空间填充设计的实验点的安排没有特定的位置要求,只需满足某些设计准则即可。其实验点安排较为灵活,而且实验次数n与参数个数m无关,不会出现所导致的“维数灾难”,较适用于复杂作用关系过程的实验设计与建模,代表性的方法包括LHS、均匀设计等。
假设输入因子的个数为m,实验次数为n(n>m),LHS首先将可行域均匀分成nm个超立方体的子区域,选取其中的n个子区域,使所有子区域都能够不重叠地投影在每一个维度上;而后在各个子区域内随机选取一个点组成n个实验点。LHS具有操作简单、样本量小、不易导致维数灾难等优点。但LHS是一种分层随机抽样方法,在某些情况下,生成实验点的随机性与均匀性不高,实验设计的效果有待提高。
2 方法研究
2.1 基本思路
由上述分析可知,LHS的实验点的个数与在各因子维度上的投影较为均匀,但这并不意味着该实验设计方式对于复杂的计算机仿真过程具有良好代表性。首先,对于因子个数为m的LHS设计,若在nm个子区域中随机选择n个子区域安排实验点,则共有nm-n个子区域未被填充。当m较大时,有nm-n≫n,这样一来,虽然样本点较为均匀分散,但是相对稀疏,仍有大量的未安排实验点的子区域。其次,由于计算机仿真过程的输出特性与输入因子之间存在复杂非线性作用关系,因而输出特性在整个可行域内的分布是不均匀的,既有输出特性的变化较为平坦的子区域,也有变化较大的子区域,还有存在局部极值的子区域。显然,实验点的均匀分散并不能够刻画输出特性的不均匀变化,样本点的利用效率不高。
事实上,为提高实验设计的效率,应该根据子区域内输出特性的变化情况有针对性地安排实验点的数目,对于输出特性变化较大的子区域多安排实验点,而对于输出特性变化较小的子区域少安排实验点。进一步地,在没有过程先验知识的情况下,可以采用对称(即各因子水平数均相等)的正交设计来初步探知输出特性在可行域内的变化情况。根据正交设计的理论,对于一个因子数为m,各因子水平数均为q,实验次数为n的对称正交设计,有n=qm-p,1≤p≤m-2,因此实验点在每一个因子的每一个水平上的投影均有重复,且重复次数为n/q。那么根据这n/q次重复即可估计出在该水平处过程输出特性的方差,而方差变化较大的水平处则提示该因子水平附近过程输出特性的变化较大。据此识别出过程输出特性变化较大的子区域,在该子区域内采用样本量较小的LHS实验设计,即可在降低样本量同时,提高实验设计效率及模型性能。
2.2 实现步骤
根据上述分析,这里提出基于正交设计与LHS的计算机实验设计及建模方法如下:
Step1:根据输入因子的个数m及问题规模,确定正交设计的各因子的水平数q,利用正交表,选择合适的正交设计集POD:

Step2:根据正交设计POD,运行计算机仿真代码,获得初始样本集:
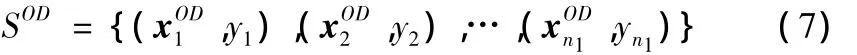

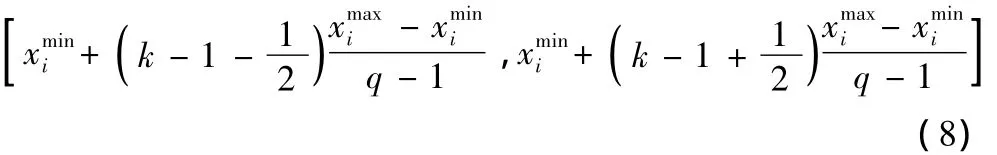
Step4:将各因子维度上过程输出特性变化较大的区间进行组合,确定需要进行LHS设计的子区域X*;
Step5:在子区域内X*安排适当数目的LHS实验点,运行计算机仿真代码,获取补充样本集:
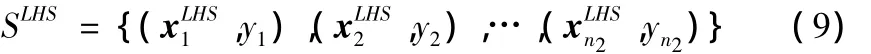
Step6:根据样本集SOD∪S,拟合计算机仿真过程的Kriging模型。
3 算例研究
3.1 仿真算例
为考察方法的性能,这里给出了一个较为复杂的算例。设计算机仿真过程的输入输出之间存在如下关系:
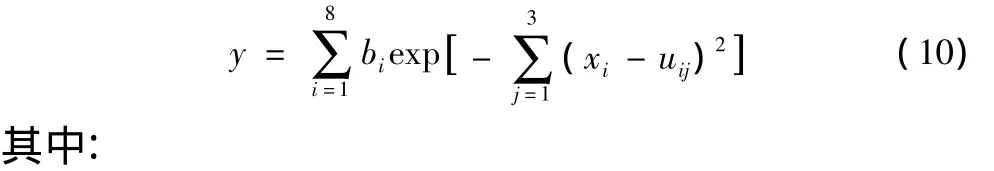

图1给出了在x3= -3,0,3时,y关于x1,x2的等高线图,可以看出,这是一个典型的非线性复杂作用关系过程。

图1 过程的等高线图
为说明方法的性能,选择与实验设计样本集不同的测试样本集:

令yi代表测试样本集的实际输出,^yi代表Kriging模型对于测试样本集的预测输出,则预测误差可表示为:

采用如下指标评价模型的性能:
(1)预测的均方误差

(2)预测误差的标准差
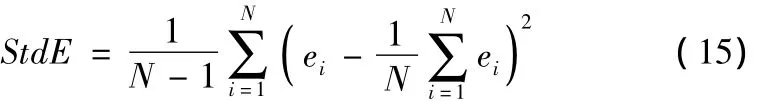
(3)预测的最大绝对偏差:

3.2 计算机实验的结果
按照3.2所示步骤,首先选择L50(51121)正交表的前3列作为正交设计的实验点集,如表1所示。表1还给出了正交实验点及对应的输出特性值。图2给出了各因子维度上5个不同水平处的过程输出特性的样本方差,在x1、x3的维度上各有一个局部极值,而在x2的维度上有两个局部极值。进一步,可以根据式(8)确定了各因子维度的包含过程输出特性方差极值的区间,分别为:

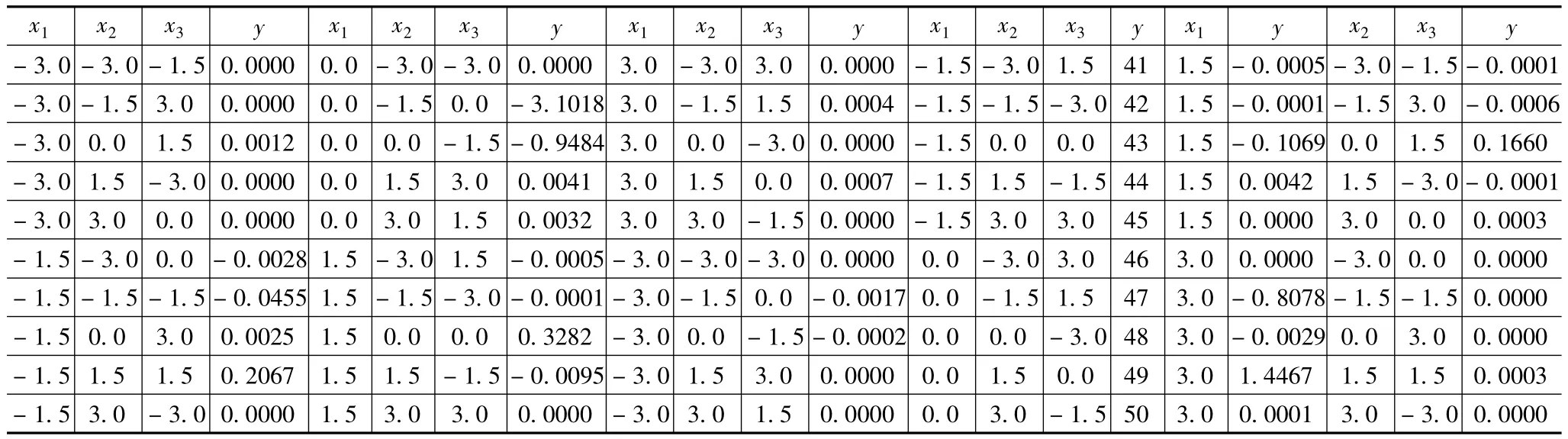
表1 第一阶段的正交设计实验点及输出特性值

图2 各因子水平处的输出特性的样本方差

图3 两阶段设计与传统LHS的实验点对比(样本量 =80)
而后在上述两子区域内添加样本量大小相同的LHS实验点。为说明方法的性能,选取了不同样本量大小(n2=10+10,n2=15+15,n2=20+20)的LHS设计,与原有的正交设计组成样本集,而后采用Kriging方法进行建模。作为对比,单纯地采用LHS设计生成样本量相同的全部实验点集进行Kriging建模。在可行域内随机生成5000个测试样本点,利用式(14)至式(16)考察各类模型的预测性能,其对比结果如表2所示。图3给出了在每个子区域LHS样本量大小为15的实验设计点集与正交设计点集的分布,图3还给出了作为对比的样本量大小为80的LHS设计的实验点集的分布。
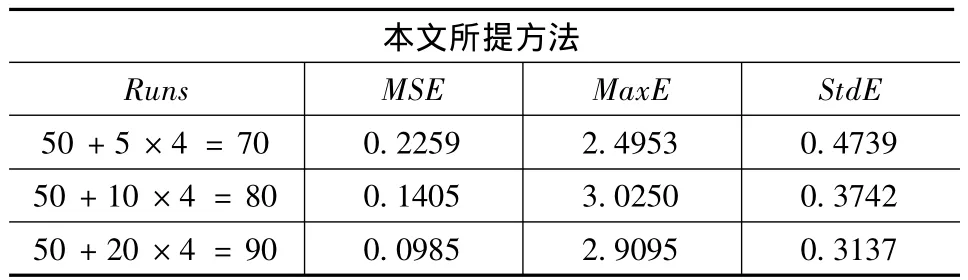
表2 不同样本量条件下方法的建模性能对比

(续表)
3.3 结果讨论
(1)关于模型预测性能。从表2可以看出,采用本文所提出的两阶段的实验设计,在样本量相同的情况下,所拟合的Kriging模型的预测性能均优于传统的LHS。具体来说,在三次对比中,所提方法的Kriging模型的MSE的均值比传统LHS的MSE的均值降低了52.4%;MaxE的均值降低了19.2%;StdE的均值则降低了28.8%。
(2)从图3可以看出,本文所提方法实验点的安排与传统LHS有显著区别。在输出特性变化较大的区域,实验点密度较高,且分布较为均匀分散,而在其他区域,实验点的密度较低,但分布较为均匀整齐。这种实验点的分布结合了正交设计与LHS的优点,使得实验点在整个可行域内的分布具有较强的均匀性和针对性。与之对比,传统LHS设计的实验点虽然在可行域全局范围内的较为均匀分散,但是并没有针对性,导致有相当数量的实验点安排在输出特性变化不显著的区域,这在很大程度上影响了模型性能。
4 结论
本文研究了计算机实验过程的小样本实验设计及过程建模方法。理论研究与仿真分析表明,对于输出特性与输入因子之间作用关系复杂的计算机仿真过程,通过正交设计可以初步探知输出特性波动较大的子区域,而后再利用LHS可以有针对性地安排实验点。在样本量相同的条件下,本文所提方法的实验设计效率与模型的预测性能均优于传统的LHS设计。
[1]冯吉路,姜增辉.基于abaqus高速切削ti-6al-4v切削状态的有限元仿真[J].组合机床与自动化加工技术,2013(2):47-53.
[2]Pronzato,L.,M?ller,W.,Design of Computer Experiments:Space Filling and Beyond[J].Statistics and Computing,2012,22(3):681 -701.
[3]Zhou,X.,Ma,Y.,Tu,Y.,et al.,Ensemble of Surrogates for Dual Response Surface Modeling in Robust Parameter Design[J].Quality and Reliability Engineering International,2013,29(2):173 -197.
[4]陈巍,周雄辉,张汝珍,等.基于kriging代理模型的注塑产品翘曲优化[J].上海交通大学学报,2010,44(4):588-592.
[5]Deng,H.,Shao,W.,Ma,Y.,et al.,Bayesian Metamodeling for Computer Experiments Using the Gaussian Kriging Models[J].Quality and Reliability Engineering International,2012,28(4):455 -466.
[6]Can,B.,Heavey,C.,A Comparison of Genetic Programming and Artificial Neural Networks in Metamodeling of Discrete-Event Simulation Models[J].Computers &Operations Research,2012,39(2):424 -436.
[7]崔庆安.面向多极值质量特性的全局式序贯性实验设计方法[J].系统工程理论与实践,2012,32(10):2143-2153.
[8]Gramacy,R.B.,Polson,N.G.,Particle Learning of Gaussian Process Models for Sequential Design and Optimization[J].Journal of Computational and Graphical Statistics,2011,20(1):102 -118.
[9]Dam,E.R.v.,Hertog,D.d.,Husslage,B.G.M.,et al.,Space-Filling Latin Hypercube Designs for Computer Experiments[J].Optimization and Engineering,2011,12(4):611-630.
[10]Fang,K.-T.,Lin,D.K.J.,Uniform Design in Computer and Physical Experiments[M].in The Grammar of Technology Development,2008:105-125.
