机床丝杠进给系统有限元热分析的热边界条件修正方法*

王万金，王 玲，刘兴业，殷国富

(四川大学制造科学与工程学院，成都 610065)

0 引言

机床热态特性分析与优化是一种减少机床热误差，提高机床精度及其稳定性的重要方法，该方法的关键是建立一个准确的机床温度场分布模型［1］。通常，机床上某些特征点的温度可以测量得到，但对于复杂结构只能测量有限点的温度值，确定整体温度场的成本很高。因此，设计中往往采用有限元法进行模拟。计算机模拟温度场的关键在于给出接近实际的热边界条件［2］。本文讨论的就是如何计算符合实际的热边界条件。

近年来，国内外学者针对有限元法热边界条件的计算做了广泛的研究。韩国的S.K.Kim等［3］运用有限元方法，建立了不同转速下滚珠丝杠进给系统随时间变化的温度场，但是由于理论计算所得的对流换热系数和丝杠螺母的发热量与实际情况相差很大，所以其有限元方法分析出来的结果与实际偏差很大。李林安等［4］以传热学理论为指导，采用试凑法，通过人工调整热边界条件，使计算结果与实测值吻合。但由于热边界条件变化范围大，因此，人工调整的工作量大，对于复杂模型不适合。阳红等［1］建立了一个模拟对流换热系数与机床温度场之间的神经网络，以实验温度场数据为该神经网络的输入量来计算对流换热系数。但是一个成熟的神经网络要经过大量的数据训练才能达到比较好的预测效果，所以该方法的计算量仍然很大。

同时，上述热边界条件计算方法都没有对热流密度进行修正，且其在计算的准确性和效率上仍不够理想。因此，本文以龙门加工中心的X向丝杠进给系统为例，提出了利用workbench多目标优化模块，以热边界条件为变量，以实验测量得到的丝杠上各点的温度值为目标，对理论计算得到的热边界条件进行修正的方法。最后，该方法应用于对某企业开发的龙门加工中心X向丝杠进给系统的温度场的仿真，得到了准确验证。

1 X向丝杠进给系统热学实验方法

1.1 X向丝杠进给系统结构

该龙门加工中心X向丝杠进给系统从左往右依次由左丝杠座、丝杠、旋转螺母系统(包含了旋转螺母、左右推力球轴承、左右深沟球轴承、螺母座和皮带轮等)和右丝杠座等零部件组成，如图1所示。该系统驱动采用丝杠固定、螺母旋转的方式：通过电机带动与旋转螺母固定的皮带轮，使旋转螺母在丝杠上运动。这种驱动方式的主要优点是螺母转动惯量小，明显改善了伺服进给系统的动态特性和节省了能源。

图1 X向丝杠进给系统结构

1.2 X向丝杠进给系统热学实验

本热学特性实验主要目的是采集X向进给系统的温升值。

实验条件：机床X向进给速度8000mm/min，其他方向静止不动。

实验设备主要有：温度巡检仪、热电阻、水银温度计、红外线温度测量仪。温度测量点分布如图2所示，热电阻用于测量固定点丝杠两端T1和T3的温度，红外线温度测量仪用于测量丝杠中部T2的温度，水银温度计测量环境温度T4。

图2 温度测量点分布图

实验开始时，丝杠螺母在丝杠最左端，实验测试时间80min，测得数据见表1，环境温度为16℃。

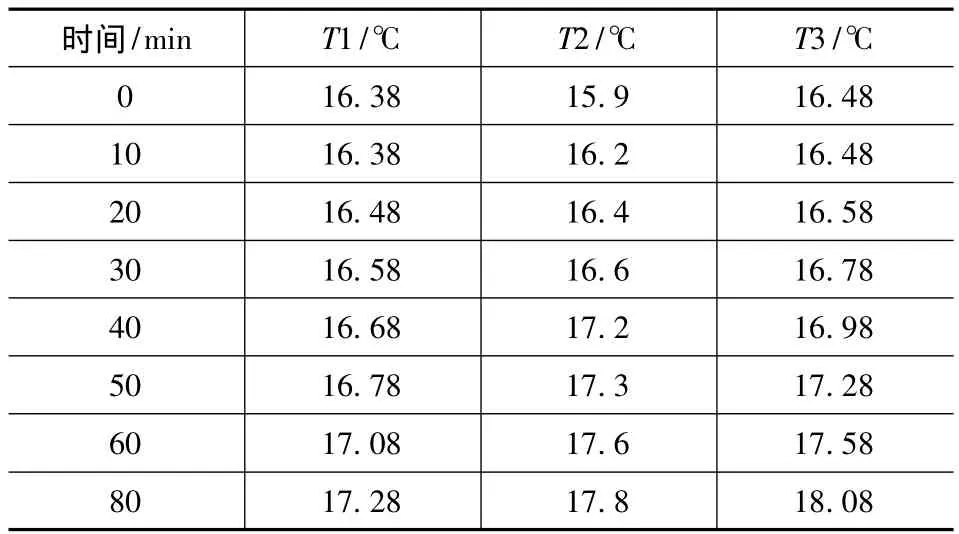
表1 测量点实际温度

2 X向丝杠进给系统有限元分析模型

2.1 丝杠进给系统模型的简化及网格划分

本文将丝杠进给系统划分成14段，如图3，A1和A14为丝杠两端固定部分，A2到A13为丝杠有效行程部分。为了便于有限元分析，对丝杠进给系统模型做了必要的简化，忽略了丝杠上的螺纹槽、退刀槽和倒角等，把丝杠简化成一个狭长的圆柱体，如图4。在丝杠进给系统中，左右丝杠座与丝杠两端固定，且跨度很大，对整个系统温度场分析影响很小，在分析时可将其视为一体，分别简化为图4中F1和F14。选择solid70热分析单元，以螺母长度为单位采用扫掠的方式划分网格。

图3 丝杠进给系统分段图

图4 丝杠进给系统有限元分析简化模型

2.2 材料参数

丝杠的导热系数为 36.5W/(mK)，密度为7820kg/m3，比热容为 460J/(kg℃)。

2.3 有限元模型加载

在丝杠实际工作过程中时，螺母与丝杠接触，轴承和螺母的发热传入丝杠。在热分析时可以将轴承和螺母的发热等效为相应的热源载荷［5］，以热流密度的形式施加在丝杠上。另外，由于丝杠螺母与丝杠之间存在温度差，且在升温阶段各段丝杠温度并不一致，由传热学理论可知，流入各段丝杠的热流密度并不完全一样，因此本文引入了一个热流密度修正系数。具体做法：引入一个以25℃为参考温度的对流换热系数ε施加在丝杠有效行程内，作为热流密度修正系数。

在X向丝杠进给系统有限元分析时，其加载时基于以下假设：

(1)在丝杠螺母移动过程中，丝杠和丝杠座对流换热系数恒定不变。

(2)润滑剂的热传导忽略不计。

2.3.1 初始热生成率计算

X向丝杠进给系统的热源来自于旋转螺母系统，分别为旋转螺母、左右推力球轴承和左右深沟球轴承，其具体计算可参考文献［6］，经计算得流入丝杠的热流量为40W。

通过(1)式可以计算得到丝杠的热流密度，经计算得丝杠的热流密度为490W/m2。

其中Q为流入丝杠的热流量，S为丝杠螺母与丝杠的接触面积。

2.3.2 初始对流换热系数计算

影响对流换热系数h的主要因素有很多，把一切对对流换热有影响的因素都放在这个参数中考虑［2］：

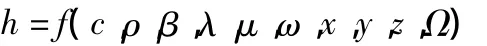
式中，c为比热容ρ为密度β为容积膨胀系数λ为导热系数μ为动力粘度系数ω为流速，x，y，z为坐标Ω为壁面几何形状。对流换热系数作为一个经验参数，复杂而难确定。目前对流换热系数的主流求法是利用相似原理进行求解，其具体求解可参考文献［7］。经计算F1和F14上对流换热系数为9W/(m2K)，F2到F13对流换热系数为7W/(m2K)。

利用上面理论计算得到的热边界条件进行有限元热分析，其分析结果与实验数据相差很大。符合实际的热边界条件是提高有限元分析结果准确性的关键。针对该问题，下面利用workbench多目标优化模块，根据实验数据，将对理论计算得到的热边界条件进行修正。

3 热边界条件修正方法

在该滚珠丝杠进给系统中，丝杠静止不动，丝杠螺母在丝杠有效行程内往复运动，且其往复运动速度很快，于是有限元分析模型加载时可以简化成旋转螺母系统产生的热流密度均匀地施加在丝杠有效行程内(图4中F2至F13部分)。热边界条件修正方法具体如下：

(1)根据实验0时刻所测的丝杠各部分初始温度，在workbench稳态分析模块中，对F1部分施加温度T1，对F7和F8施加温度T2，对F14施加T3温度，进行稳态分析获得瞬态分析的初始条件。

(2)根据计算得到的热边界条件进行瞬态分析，观察分析结果与实验结果的差异。

(3)利用workbench多目标优化模块，以丝杠对流换热系数、热流密度、热流密度修正系数为变量，以实验测得的10min、30min、50min和80min时T1和T2的值为目标，来修正上述热边界条件。其中，以计算得到热边界条件50%～200%作为该热边界条件的变化范围。

(4)将优化后所得到的热边界条件加载到workbench中的瞬态分析模块中，比较有限元分析结果和实验结果的差异，分析结果见图5，其中FEM代表有限元法，MEA代表实验法。

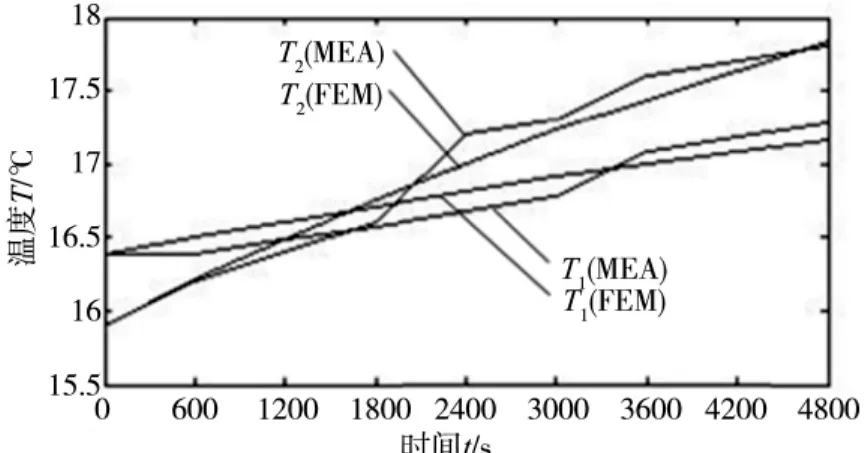
图5 简化有限元法和实验法所得温度曲线对比

从图5可以看出，经拟合后温度曲线与实际温度曲线大致一致，拟合效果较好。但是，在丝杠系统在实际运行中，丝杠螺母往复移动，即热源在移动，所以丝杠的温度在一个周期内的变化趋势是升温、降温再升温的过程，而上述有限元分析法在施加载荷时做了简化处理，导致了其分析结果不能完全真实地反应滚珠丝杠的瞬态分度场。所以，下面将在ANSYS经典环境中，利用修正后的热边界，施加移动载荷［8］，进行有限元分析。

4 计算结果与分析

在图4有限元简化模型中，以螺母长度为单位，将丝杠有效行程部分划分成12段(F2到F13)。然后对其施加移动载荷，具体步骤如下：

(1)根据X向进给速度，计算一个行程内每段上热边界条件作用时间(本文中丝杠有效行程为4m，进给速度为8000mm/min，故移动热源每2.5s移动一次)。

(2)从左端F2开始到右端F13，再从右端F13到左端F2，以2.5s为载荷步时间依次施加移动热源，在施加移动热源过程中，对应段施加热流密度h，对应段的前一段施加热流密度补偿系数ε，其他段施加对流换热系数C，如图6在F5上施加移动载荷。

(3)利用DO循环，重复2过程80次，完成瞬态热分析。

图6 移动载荷作用图

图7为有限元法和实验法所得T1和T2的升温曲线的对比。为了便于观察，图8提取了有限元法和实验法所得T2在0～600s的变化曲线。从图中可以看出，有限元法分析得到的温度变化趋势与实验结果所得基本一致，其绝对误差见表2。由表2可知，有限元法最大误差为0.15℃，而试验中所用测量温度的红外线温度测量仪的精度为0.1℃，故有限元法比较准确地仿真了丝杠进给系统的瞬态温度场。

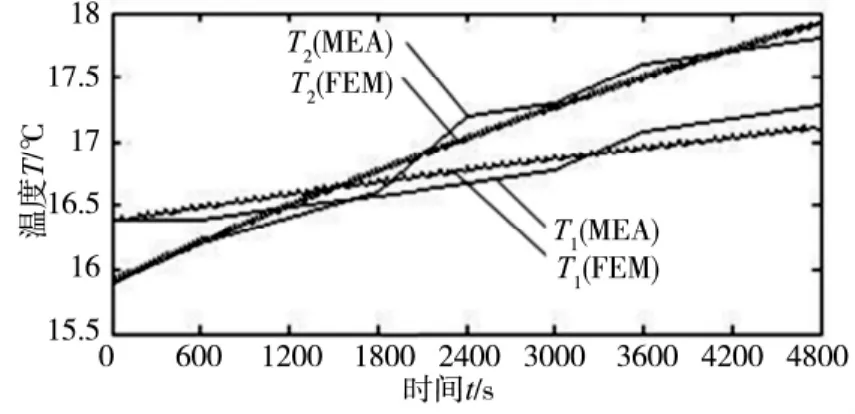
图7 有限元法和实验法所得温度曲线对比

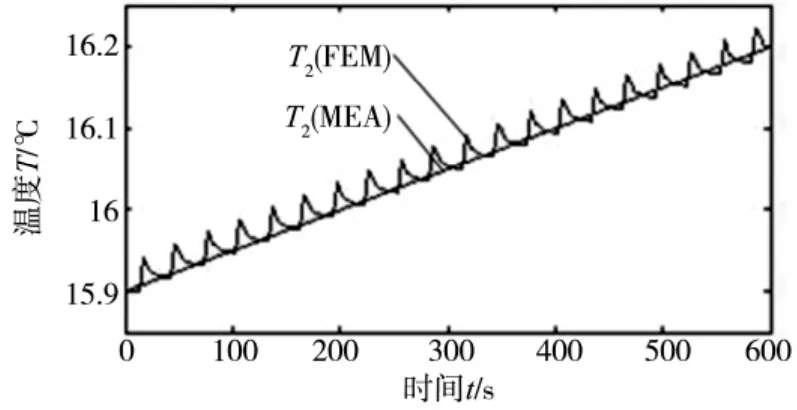
图8 有限元法和实验法所得T2温度曲线对比

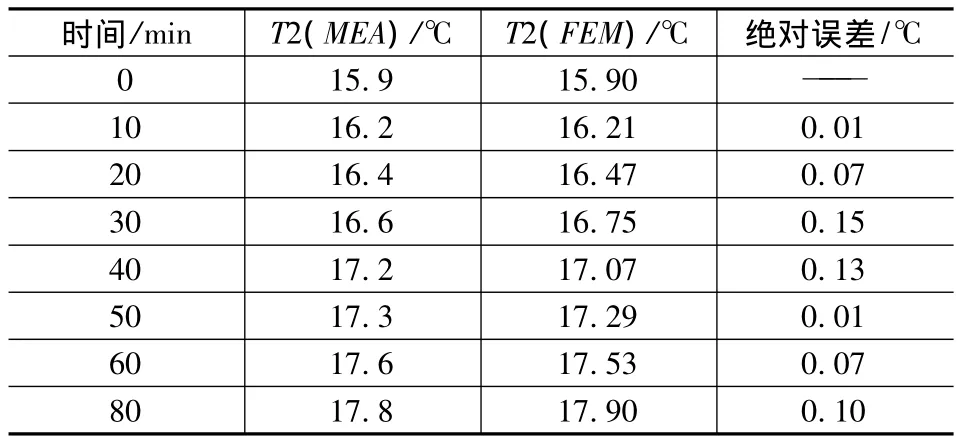
表2 T2处有限元法和实验法温度对比

5 结束语

本文提出的在workbench优化模块中，利用实验结果修正热边界条件的方法具有以下2个特点：

(1)提高了有限元法瞬态温度分析的精度。该方法避免了因实际工况的复杂性，计算得不到准确的热边界条件。

(2)减少了工作量，将繁琐的热边界条件的修正交给计算机来实现。

上述特点表明，该方法适用于机床类似零部件的热态分析，具有很强的实用价值。

［1］阳红，殷国富，方辉，等.机床有限元热分析中对流换热系数的计算方法研究［J］.四川大学学报(工程科学版)，2011，43(4)：241 －248.

［2］张延蕾，佟维.对流换热系数的反求方法［J］.大连铁道学院学报，2005，26(4)：25 －28.

［3］Kim S K，Cho D W.Real-Time Estimation of Temperature Distribution in a Ball－ screw System［J］.International Journal of Machine Tools and Manufacture，1997，37：451 －464.

［4］李林安，佟景伟，李鸿琦，等.非对称活塞稳态温度场的三维有限元分析［J］.天津大学学报，1995，28(1)：107 －112.

［5］王大伟，刘永红，张龙，等.基于有限元法的滚珠丝杠传动过程中的温度场和热变形仿真［J］.计算机辅助工程，2009，18(2)：29 －33.

［6］何震.机床滚珠丝杠系统热特性分析及其热变形补偿［D］.成都：西南交通大学，2009.

［7］曹红奋，梅国梁.传热学：理论基础及工程应用［M］.北京：人民交通出版社，2004.

［8］邢静忠，王永岗，陈晓霞.ANSYS7.0分析实例与工程应用［M］.北京：机械工业出版社，2004.