基于随机Petri网的连续型制造系统建模与性能分析
2013-09-12潘隆涛涂海宁
潘隆涛,涂海宁
(南昌大学机电工程学院,南昌 330031)
0 引言
近几年在国家产业政策的鼓励下,我国某新型材料工业取得了较大的进步,本文以A作为其中某产品代号,A产品作为典型新型材料其中的一种,其生产技术也逐步成熟稳定[1]。基于对A产品制造过程的调研与分析,建立基于Petri网的过程制造系统模型,分析其内部存在的问题并优化生产过程控制。目前在国内该领域还没有较为完整的优化方案和整改案例,而国外的许多大型ERP系统已经部署到新型墙材生产领域,因此本文对该领域的研究十分必要。Petri网[2]是一种形式化建模技术,该概念早在1962年就由Carl Adam Petri提出;Petri网模型分析主要包括状态的可达、位置的有限、变迁的活性、标识之间的可达等等;故Petri网理论较为适合连续型流程式生产的描述与研究,本文将结合现场实际数据分析PN模型特性并加以优化。
1 连续型制造系统调研
1.1 工序、设备等生产因素调研
A产品规格种类较多,本文基于A产品制造企业长期的企业生产调查和信息收集,并对系列产品中较为典型的A产品生产进行介绍,如图1为A产品的现场生产线示意图,其关键工序为物料制备、压制成型、蒸压养护,故其关键工序所在的设备必将受到重点看护,设备包括搅拌机、球磨机、轮辗机、压机、蒸压釜。除主要设备外,物料搬运需要斗式提升机、皮带运输机、布料机、摆渡车、码垛车等若干[3]。

图1 现场生产线示意图
1.2 加工工艺过程信息调研
某连续型制造系统生产过程较为固定,从A产品生产线的原料流向角度而言,原材料(粉煤灰、石灰、石膏)进行辗压、搅拌、混合而成,再经成型压制,最后通过蒸压养护而成[4];生产过程中各工序需要控制单位加工时间(即单位速率),如图2。

图2 A产品生产工艺流程图
(1)物料配制:主要包含原料仓输出量的连续动态测量,保持混合料的混合配比比例满足一定的正态分布,偏差在规定范围内;而物料配制阶段较容易控制,故物料配制需要经常调整来满足之后的生产工序要求变化。
(2)压制成型:压制的控制参数有压机压力、成型半成品的尺寸规格和缺角情况。
(3)蒸压养护:蒸压釜是一种有爆炸危险的压力容器,因此生产时需要控制釜内的压强和蒸汽量,保持升温、恒温、降温三阶段时间段的压力满足规定;此外,还需要对出釜的砖进行前期良好养护,避免受到恶劣环境的影响。
2 生产现场单位加工相对速率计算
根据A产品生产线各加工工序用料量和生产设备加工周期等数据可以计算出一下各工序用时情况;如公式(1)~(4):

计算额定产量为120块压机的用时约为46min,原料配比时密度可知约为555~700kg/m3,成型蒸养过程挤压缩水率为0.2,故配料后体积为24/(1-0.2)=30,G蒸压釡加工量=600kg/m3×30m3=18t,型号为PEW400X600的中小型颚式破碎机额定生产能力约为54t/h,T破碎=18/54=20min,同时可计算T搅拌=((18t/h/20t/h)*60min)/5min=10.8min,额定产率均约为110t/h的配料加工、球磨加工用时T配料计量=9.818min,T球磨=9.818min,T胶结≈18min,T消化≈25min,产率为20t/h的DHLl600行星式轮碾混合机T轮辗≈13.5min。故各工序加工速率集合为{30,62,34,62,56,24,45,14,1}。
3 随机Petri网的系统模型建立
3.1 随机Petri网定义
随机Petri网是一个五元组SPN=(P,T,F,M,λ),在原型Petri网(P,T,F,M)中,加入变迁集T上的时间函数定义 λ,而设T={t1,t2,…tm},则λ(ti)=λi为一个非负数,表示在变迁ti的发生速率。故变迁的平均时延为:
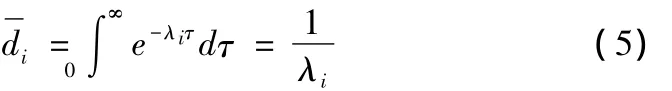
任何生产制造系统都具有生产的不稳定性,设Σ=(P,T;F,M0,λ)为某连续型制造系统生产系统的随机Petri网,变迁的发生速率集合 λ=[λ1,λ2,…,λ9](n=|T|),单位为标量加工次数/h。
3.2 模型建立
根据本文以上的工艺信息和生产设备信息介绍,将A产品进行Petri网模型构建,构建如图3、图4:库所集合P=(p1,p2,…p34),变迁集合T=(t1,t2,…,t34)。
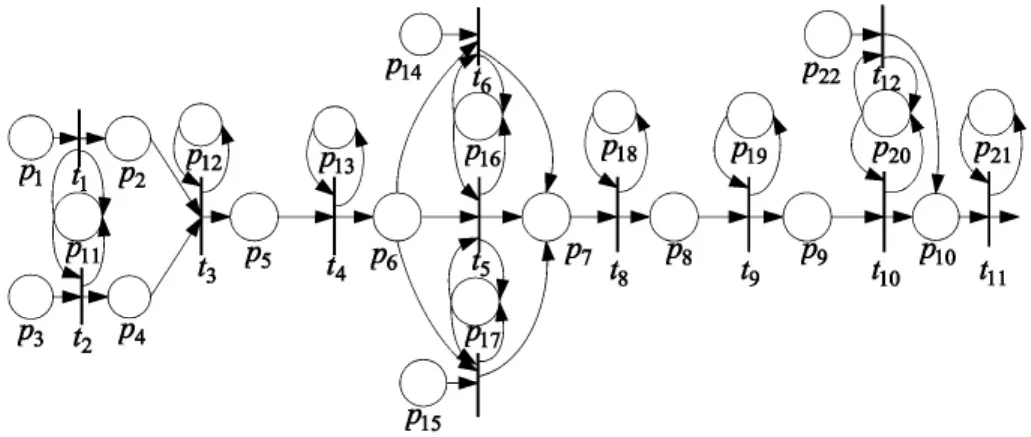
图3 配料阶段Petri网

图4 成型蒸养阶段Petri网
3.3 模型化简
根据上文建立的A产品Petri网模型,以主要工序与设备为基点进行模型化简,如斗式提升机,皮带机都可由向后的规则,依次将在这类搬运上的损耗时间加入其后的库所内,统一进行变迁速率的计算,如图6为化简后的A产品生产过程Petri网模型;表1为该模型对应的库所、变迁功能定义的表示。

图5 A产品生产Petri网模型
4 A产品生产线性能分析


图6 广义随机生产系统PN网

图7 同构的马尔科夫链

图8 minitab折曲线
根据原材料的流向和标识下库所单位托肯数量变化,总结得式(6),即;

4.1 求解标识稳定状态概率
集合={p1,p2,p3,…,p9}为9 个状态标识的稳态概率,转移矩阵为Q,即:
Q=[qij]r×r

式(7)称为∑的概率转移矩阵,其中qij满足式(8):
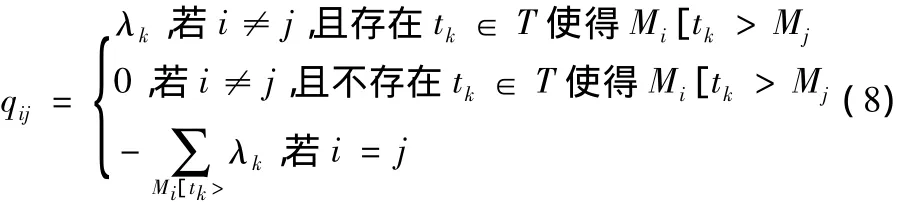
由MC平稳分布的相关理论可得式(9):

将矩阵P*和矩阵Q分别代入上式计算,利用matlab求解得:

4.2 求解变迁利用率
设U(t)为∀t∈T的利用率,即为变迁t可实施的所有状态的稳态概率之和,如式10。

E是使t可实施的所有可达状态集合。故:

5 结论
利用minitab分析数据可知图8为minitab折曲线,各标识M稳态概率变化幅度不大,而在设备加工预定状态下其工序7也就是蒸养加工历时较长而设备利用率较高,结合现场生产情况分析,在预定的生产线增加2台蒸压釜,单位加工时延降低,有效降低了生产单周期用时,降低了蒸压釜故障发生率,minitab折曲线提高了产品生产效率。
[1]张爱国.我国蒸压新型墙材制品生产现状及发展趋势综述[J].砖瓦,2010(8):53-56.
[2]Suraj Z,Fryc B,Matusiewicz Z,等.A Petri Net System-an Overview[J].Fundamenta Informaticae,2006,71(1):101-120.
[3]蔡祖光.粉煤灰蒸压高强砖的生产技术及其关键生产设备[J].砖瓦,2007(12):5.
[4]陶有声.蒸压粉煤灰砖及蒸压灰砂砖生产技术及发展[J].砖瓦,2005(7):9-13.
[5]丁峰.有色时间 Petri网与随机Petri网应用研究[D].2009.
[6]田立勤,林闯,周文江.随机Petri网模型中变迁的串、并联性能等价化简技术[J].电子学报,2002,30(8):1134-1136.
[7]何炎祥,沈华.随机Petri网模型到马尔可夫链的转换规则与实现[J].计算机科学与探索,2013(1):55-62.
