基于多体理论的直驱转台精度分析优化*

周玲莉，王禹林，冯虎田

(南京理工大学机械工程学院，南京 210094)

0 引言

数控直驱回转工作台作为各类精密数控机床的关键零部件，其工作精度对机床的整体加工精度有着重要的影响。因此对其进行精度设计是非常必要的，也是优化设计的重要环节。

精度设计可以分为精度分析与精度分配两个互逆的过程，要对回转工作台进行精度分析首先必须建立其误差模型，本文主要进行回转工作台的空间几何误差分析，不考虑其受热变形以及受力变形产生的误差，所以只针对其空间几何误差进行讨论。在机械结构空间几何误差建模方面，世界各国专家学者经过多年研究已经发展出误差矩阵法、机构学建模法、刚体运动学法等多种建模方法［1］，而多体系统理论由于其约束条件少、规范化等特点，亦被用于机械结构误差建模和补偿，以及解决复杂系统运动等问题［2］。刘又午等人［3-4］就曾利用多体系统动力学理论对多轴机床建模进行了系统的研究，并且已经获得很多成果。但是在回转工作台精度分析方面，目前借助多体动力学方法进行精度分析的例子还很少，都是以传统的建模方法为主。精度分配的主要方法有尺寸链理论法［5］，蒙特卡洛法［6］等，此外康方等人［7］以降低成本为目标，提出了一种机床精度优化分配方法的思路，Wang等人［8］则为螺杆转子磨床精度分配建立了一种多目标参数优化模型。这些工作都将为回转工作台制造精度和成本的综合优化提供有益帮助。

基于多体系统理论建立的数控直驱回转工作台的误差模型，能够描述回转工作台各个组成部分的误差是怎样通过结构关系以及相对运动转化成最终整体的定位误差，由此可以定量分析出各类基本误差对整体加工误差的影响情况，从而为回转工作台的精度分配、设计优化等工作提供理论依据。

本文基于多体系统理论，分析数控直驱回转工作台的拓扑结构，建立其空间几何误差模型，进而综合考虑回转工作台整体精度和制造成本，建立其精度分配优化模型，以满足不同的优化目标，最后给出了提高精度控制成本的措施和建议。

1 直驱回转工作台精度误差建模

1.1 直驱回转工作台的拓扑结构

该高精度直驱数控回转工作台的内部结构如图1所示，其有一条结构主线：底板—电机—转台面。假设底板为1号物体，根据多体系统的编号方法，沿远离底板的方向，按照自然数的增长，依次标定各个部分的序号为：1底板，2电机定子，3电机转子，4转台面。通过分析该系统各部分的结构关系得到其多体系统拓扑结构图以及各物体编号如图2所示。惯性参考系R设在地面上。

图1 回转工作台总体结构图

图2 该回转工作台的拓扑结构图

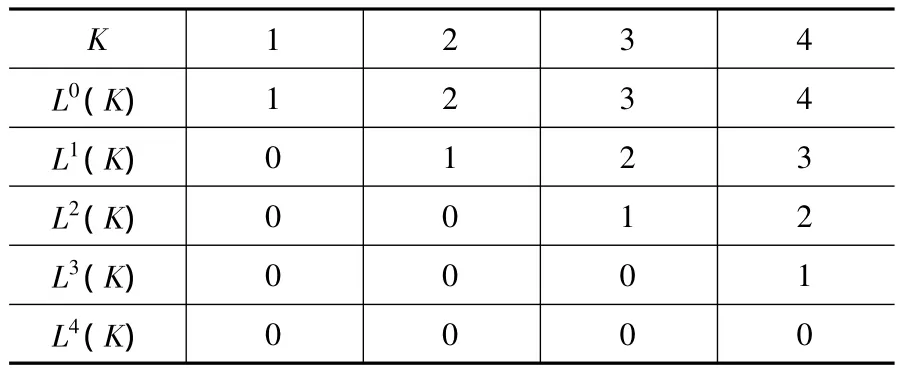
表1 该回转工作台的多体系统低序体阵列

表1中列出了该高精数控直驱回转工作台多体系统的各低序体阵列，表中K为该回转工作台多体系统中各物体的编号，Ln(K)为物体K的n阶低序体的编号，L为低序体算子。

1.2 直驱回转工作台的几何误差描述

为了简化计算，对回转工作台多体系统模型各坐标系进行设定：在所有物体上建立与其固联的直角坐标系称为子坐标系，各子坐标系的X、Y、Z轴方向按照右手定则确定，并且各子坐标系的X、Y、Z轴方向分别对应平行。

由于该回转工作台采用轴对称结构，同时只有一个运动为绕Z轴的转动，所以对该回转工作台进行误差建模时，仅需要考虑转台面绕Z轴转动(γ为转动角度)所引起的各项空间几何误差，所建误差模型中共包括6项几何误差参数［9］，见表2和图3。

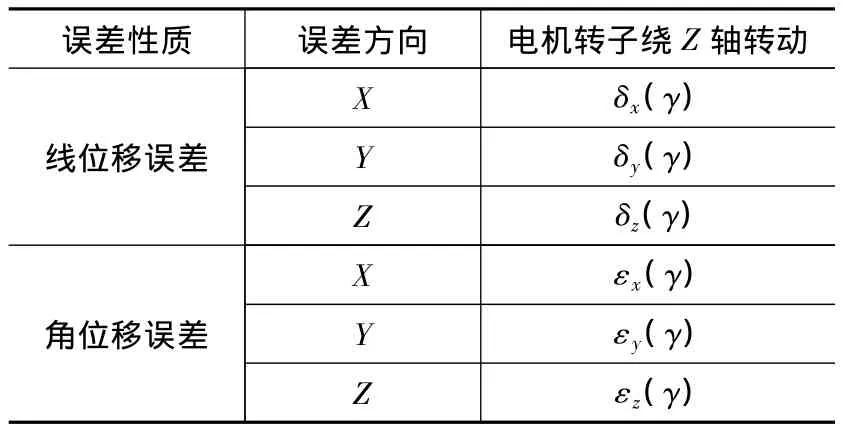
表2 该回转工作台的6项几何误差参数

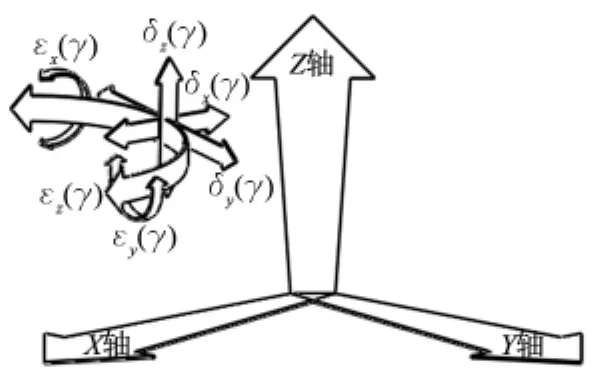
图3 该回转工作台的6项空间误差描述示意图

该回转工作台理想状态下的系统拓扑模型如图4所示，考虑上述6项空间几何误差的系统拓扑模型如图5所示，各部分主要考察其位移误差以及位置误差。在底板B1上设置惯性参考系R，在各低序体上设置相邻高序体的运动参考点Qn，通过固联在低序体上的理论位置矢量qn来描述高序体Kn相对于相邻低序体上子坐标系原点的位置，位置误差矢量用qne表示，动坐标系Rn固定在高序体Kn上，通过Rn的坐标原点相对Qn的理论位移矢量Sn来描述高序体Kn相对其相邻低序体的运动，位移误差矢量用Sne表示。

图4 理想状态下该回转工作台多体系统拓扑模型

1.3 直驱回转工作台相邻变换矩阵

一般的多体系统，都可以借助4×4阶Denavit-Hartenberg变换矩阵来描述，它可以同时表明各物体之间的位置以及角度关系，使后期数据处理分析更加方便，下面列出基于图5所示的回转工作台多体系统误差模型的各相邻变化矩阵。式中，［ASV］p为理想状态下相邻体间的位置变换矩阵，［ASV］pe为实际状态下相邻体间位置误差变换矩阵，［ASV］s为理想状态下相邻体间的位移变换矩阵，［ASV］se为实际状态下相邻体间位移误差变换矩阵，其中：体V是体S的相邻高序体。O为惯性参考系原点，K1为电机定子，K2为电机转子，K3为转台面。建立各相邻体之间的变换矩阵如下：

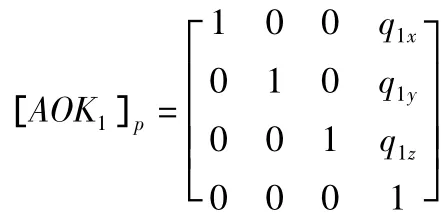
(参数为电机定子体坐标系在底板体坐标系中的位置)

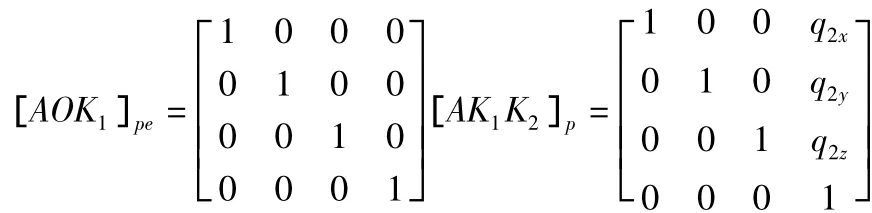
(参数为电机转子体坐标系在电机定子体坐标系中的位置)

(参数为转台面体坐标系在电机转子体坐标系中的位置)

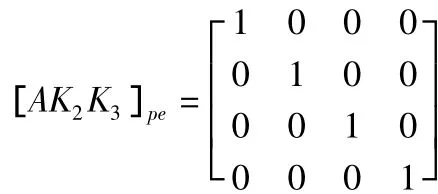
1.4 直驱回转工作台的误差模型

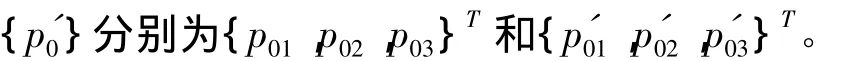
则{p0}可表示为：

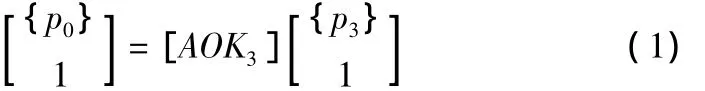
其中［AOK3］为理想状况下，转台轴承体坐标系R3与惯性参考系R之间的理论变换矩阵，且：

其中：V=Lt(K)，S=L(V)，Lu(K)=1;

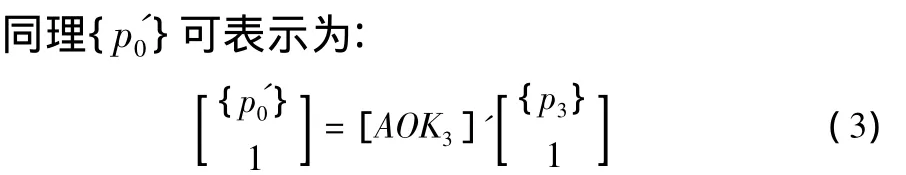
其中［AOK3］'为有误差情况下，转台轴承体坐标系R3与惯性参考系R之间的理论变换矩阵，且

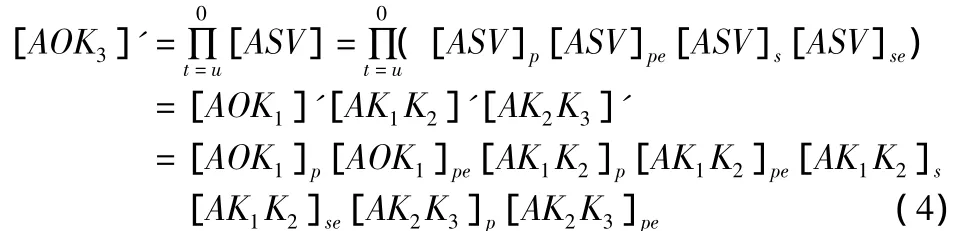
如果误差不存在，那么{p'0}应该与{p0}相同。但是在实际的生产加工过程中，误差的出现总是不可避免的，使得P点的实际位置坐标{p'0}与理论位置坐标{p0}存在偏差。令{e}为P点实际位置坐标和理论位置坐标的误差，则有：

此即为该高精数控直驱回转工作台的误差模型［10］。

2 直驱回转工作台精度分配优化

高精数控直驱回转工作台设计的主要目标是“高精”，这不仅仅是要求回转工作台各部分的精度要高，而且要高的合理，否则盲目提高一些不必要的精度要求，不仅不能使回转工作台的整体加工精度提高，还会导致无谓的成本浪费。前面一节已经对高精数控直驱回转工作台进行了误差建模，下面在此基础上对其进行精度分配优化，利用数学建模知识建立其精度分配目标函数，在满足设计精度要求的前提下，根据实际需要对各零部件的精度进行优化分配，使回转工作台的精度与经济性能够得到良好的统一。

2.1 设计变量

从之前的分析中可知，该高精数控直驱回转工作台共有6项几何误差参数，其中3项角位移误差与3项线位移误差之间并不是相互独立的，可以相互转换，因此可以对其进行简化，得到互相独立的参数，更加便于计算。角位移误差与线位移误差之间的转换公式为：

式中：D—电机转子的直径，279mm;

H—电机转子的厚度，63mm。

故直驱数控回转工作台精度优化模型仅以3项线位移误差为设计变量：

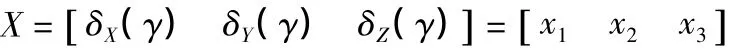
2.2 目标函数

以降低该高精数控直驱回转工作台的制造成本和满足X、Y、Z三个方向上的整体精度为目标，建立回转工作台的精度分配数学模型［11］为：

minf(x)=t·A+(1 －t)·B

式中：A—整体精度项;

B—成本项;

t—精度权数(0≤t≤1)，t的取值越大，则目标越倾向于提高整体精度，反之，则越倾向于降低生产成本;

ex、ey、ez—回转工作台在三个方向上的精度目标值，通过回转工作台设计变量及其误差模型求得;

ex0、ey0、ez0—回转工作台在三个方向上的精度经验值，通过回转工作台设计变量经验值及其误差模型求得;

ai—公差特征指数，取ai=2;n—设计变量数，取n=3;

xi—设计变量公差带的一半;

xi0—设计变量经验值公差带的一半;

ki—设计变量的成本权数。假设各几何误差参数对成本的影响程度相同，根据角位移误差与线位移误差的转换公式，εy(γ)与 δx(γ)相关，故有2个几何误差参数与设计变量x1相关，因此x1对该回转工作台的成本权数k1取为2/6=0.3333，同理可得k2和k3分别为 0.5和0.1667。

2.3 约束条件

(1)在进行精度分配优化之前，首先要确定回转工作台在X、Y、Z三个方向的总体精度均要满足预定的精度要求［ex］=0.05、［ey］=0.05、［ez］=0.008，即：

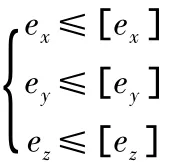
(2)另外，对于回转工作台的单个几何误差参数而言，比如δx(γ)，其精度要求也不能低于X方向上的整体预定的精度要求，δx(γ)≤［ex］。即：

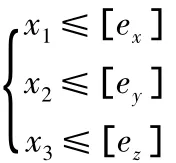
2.4 精度分配优化

根据之前的分析，在进行数控直驱回转工作台精度分配的时候，主要考虑其精度以及成本之间的关系处理。由于要想提高整体精度，就必须牺牲一定的成本，这两者之间存在一定的矛盾性，而在实际的生产中，这两者都是非常重要的，所以分别以侧重于提高精度和侧重于降低成本作为优化目标，借助Matlab软件及其遗传算法工具箱［12］对回转工作台精度分配进行优化，并与传统的设计经验值进行对比，验证优化效果。表3为两组目标的变量优化结果与传统经验值的对比，其中方案a侧重于提高精度，而方案b侧重于降低成本，设计变量经验值由某回转工作台制造厂商提供。

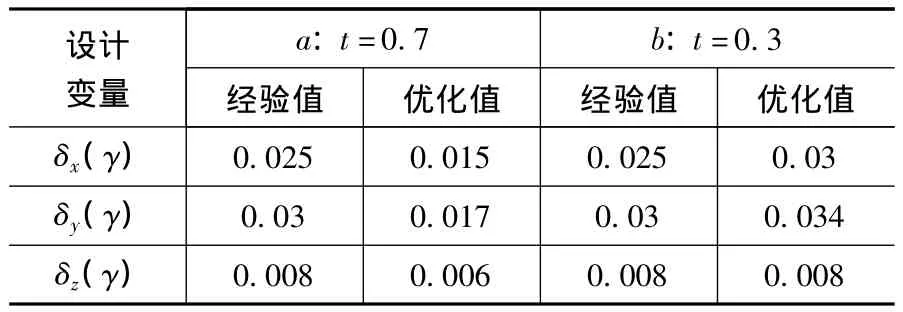
表3 变量优化结果(mm)

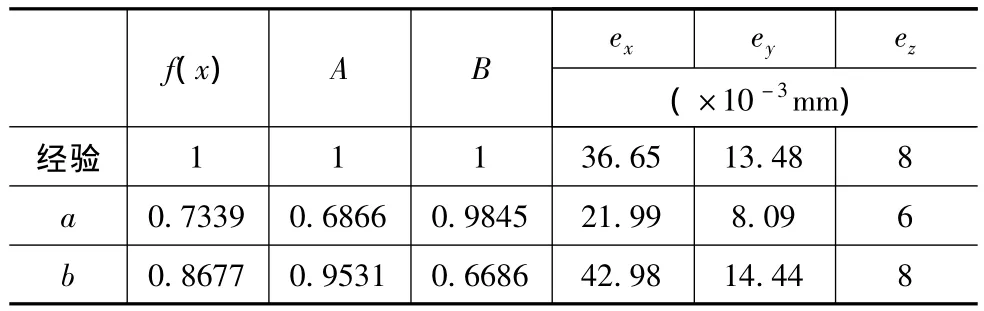
表4 优化前后回转工作台整体精度与成本比较

优化前后回转工作台的整体精度与成本比较见表4，其中A表示回转工作台的整体精度，B代表回转工作台的成本。从表3与表4中可以看出，传统的精度经验分配方法虽然能够满足回转工作台整体精度的预定要求，但是一些个体的精度分配不合理，对整体精度影响不大的方面精度过高，而对整体精度影响较大的方面精度反而不高，导致整体精度没有达到最佳水准而成本却相对较高。如表4所示方案a侧重于提高精度，优化后，工作台X方向精度值减小了：(36.65－21.99)/36.65=40%，Y方向精度值减小了：(13.48－8.09)/13.48=39.99%，Z方向精度值减少了：(8－6)/8=25%，整体精度项A也大幅度下降，说明回转工作台的整体精度得到很大提高，方案b侧重于降低成本，优化后，各方向的精度值均有不同程度的增加，而且在保证整体精度依然在要求范围内的情况下，成本项B减少了：(1－0.6686)/1=33.14%，说明回转工作台整体成本明显下降。

2.5 结果讨论

该回转工作台的6项几何误差与其零部件的对应关系如下：

(1)δx(γ)，δy(γ)对应转台面与电机的同轴度误差;

(2)δz(γ)，εx(γ)，εy(γ)对应底板接触面的平面度误差;

(3)εz(γ)对应电机定位精度的误差

通过上述分析找到的误差源主要是转台面、电机和底板，因此，转台面和底板的本身的制造装配误差以及电机的性能是影响回转工作台精度的主要因素。其中εz(γ)的变化对回转工作台精度影响最大，因此提高回转工作台精度应先从电机定位精度误差入手，这可通过选用高精度的电机以及角度测量反馈装置来实现。另外转台面与电机的同轴度以及底板基准面的平面度误差对整体的加工精度也有很大影响，所以应该通过磨削精加工接触表面，减小接触表面粗糙度，严格控制配合面的位置尺寸，并且在安装时借助垫片等工具保证各零部件的位置精度来实现整体精度的提高。

3 结论

本文首先利用多体系统动力学理论建立了高精数控直驱回转工作台的误差模型，然后通过数学建模方法借助Matlab软件及其遗传算法工具箱对其进行多目标参数优化，针对不同的要求实现回转工作台的精度优化分配，并将优化结果与实际精度指标相结合，提出改善回转工作台整体精度情况的方法。

通过多目标精度分配优化，发现该高精数控直驱回转工作台的经验精度分配方法不合理，有些方面经验值过于保守，造成了成本的浪费，而有些方面经验值却不够高，使整体精度还能进一步提升。优化之后，侧重于提高精度的方案使回转工作台三个方向的整体精度分别提高了40%、39.99%和25%;侧重于降低成本的方法使回转工作台的成本降低33.14%，满足了不同的场合需求，使回转工作台的整体性能得到很大改善。该空间几何误差模型和优化方法亦可应用于其它类似结构以及机床整机的精度分析和优化，有利于提高产品的加工精度、降低生产成本，乃至提升整个国家制造业的能力和水平。

［1］粟时平，李圣怡，王贵林.基于空间误差模型的加工中心几何误差辨识方法［J］.机械工程学报，2002(7)：121－125.

［2］朱赤洲，陈蔚芳，赵鹏，等.数控机床三维空间误差建模及补偿技术研究［J］.组合机床与自动化加工技术，2012(4)：16－19.

［3］刘又午.多体动力学的休斯敦方法及其发展［J］.中国机械工程，2000(6)：10－16.

［4］刘丽冰，王广彦，刘又午.复杂机械系统运动误差自动建模技术研究［J］.中国机械工程，2000(6)：51－55.

［5］赵学满，倪雁冰，徐淑静.并联机床关键零部件精度设计［J］.机床与液压，2004(5)：55－58.

［6］卢强，张友良.用蒙特卡洛法进行6腿并联机床精度综合［J］.中国机械工程，2002(6)：20－23.

［7］康方，范晋伟.数控机床制造精度的优化分配方法［J］.机械科学与技术，2008(5)：588－591.

［8］王禹林，陶丽佳，孙文钊，等.基于多体系统理论的螺杆转子磨床精度分析与优化［J］.南京理工大学学报，36(6)：1015－1020.

［9］粟时平，李圣怡.五轴数控机床综合空间误差的多体系统运动学建模［J］.组合机床与自动化加工技术，2003(5)：17－20.

［10］康方，范晋伟.用于精度分配的数控机床误差建模［J］.机械制造，2007(4)：9－12.

［11］Dong Z.Production cost－ tolerance models for tolerance synthesis［J］.Journal of Engineering for Industry，1994(116)：199－206.

［12］雷英杰.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.