刀库及机械手多态可靠性建模与分析*

葛玉华，韩 军，冯虎田

(南京理工大学机械工程学院，南京 210094)

0 引言

传统可靠性研究默认将系统作为二态来分析，即“正常”和“失效”，但大型复杂系统的易损零部件可更换、机械部件可维修，大部分部件的性能逐渐退化，这使得系统在工作时呈现出多种状态水平，如自动换刀过程，并不只有换刀成功与换刀失败两种状态，换刀能够勉强实现，但是效率下降、精度衰退或者平稳性变差等都是多态性的体现［1］。

1974年，Barton R M，Damon W W首次提出了多态系统(Multi-State System，MSS)可靠性的概念［2］，指的是系统不只具有“正常工作”和“完全失效”两种状态，还存在多种中间工作(或失效)状态，或存在多种中间性能水平。例如冗余系统、共载系统、可维修系统及性能退化系统等都属于多态系统的范畴。经过 Murchland J［3］、Ushako、Lisnianski等人的研究和发展，Markov随机过程理论、Monte Carlo法［4］、通用生成函数、模糊理论、二值决策理论等被陆续应用到多态系统可靠性分析中。

为定量评估刀库及机械手特定时刻的性能可靠度，掌握其在寿命阶段的性能衰退规律，采用多态系统可靠性理论对其进行研究具有较深远的意义。复杂系统由多个部件(或分系统)组成，各部件的功能不同、状态不同，因此需将部件及系统分开研究。Markov链是研究状态及状态转移随机过程非常有效的方法，但对于状态量较庞大的系统，计算极其复杂且容易犯错，因此采用Markov方法获得部件各性能状态值及其概率的对应关系，并采用特殊数学技巧——通用生成函数(UGF：Universal Generation Function)方法构建部件及系统的多态可靠性模型，大大降低了计算维度，提高了分析效率［5］。基于如上理论的多态系统可靠性建模的基本步骤如图1所示。

图1多态系统可靠性建模

1 刀库及机械手系统分析

刀库及机械手为自动换刀装置的一种，配置于大中型复合加工中心中，由刀库存储加工工序所用刀具，并在合适的时机将刀具准确送至换刀点，由机械手完成刀具在刀库与主轴之间传递交换的任务，能够缩短非加工时间、提高生产率及工件加工精度、减少机床占地面积，有助于实现加工中心的高效能、高精度、高集成。

刀库及机械手的可靠性是指其在一定的工况条件下，在规定的使用寿命内完成储刀选刀及换刀的能力。在以往的可靠性分析中，只是找出导致“换刀失败”的故障现象、原因及影响，但是在换刀成功的前提下，刀库及机械手完成换刀功能的完美度究竟是多少?如何评价呢?为解决上述问题，首先需确定最能反映刀库及机械手工作状态的性能参数，根据刀库及机械手的功能，要求换刀动作的及时性、准确性和平稳性，可知工作时间T、到位精度D和振动速度V是刀库及机械手的主要性能参数。随着换刀次数的增加，刀库及机械手的性能会逐渐衰退，在不发生重大故障或维修调整事件时，内部零部件的磨损、松动、疲劳等会使换刀时间逐渐延长、精度逐渐衰退、振动逐渐变大，表现为T、D和V的连续多态性，即刀库及机械手的性能可靠性。

刀库及机械手由储刀选刀分系统及机械手换刀分系统组成，为串联关系，两分系统的功能不同，各自性能评价指标如表1所示。

表1 系统及分系统性能评价指标

系统的结构函数指系统状态与分系统状态之间的关系，首先，利用系统与分系统性能参数之间的物理关系直接建立数学模型，如系统工作时间为选刀时间和换刀时间之和;其次，在没有明确关系时，根据刀库及机械手串联结构的特性［6］，系统状态为最差的部件状态，因此系统到位精度为分系统较差的精度，系统振动为分系统较大的振动。设系统状态为Y(n)，分系统状态为X(n)，n为换刀次数，建立刀库及机械手结构函数如式(1)、式(2)。

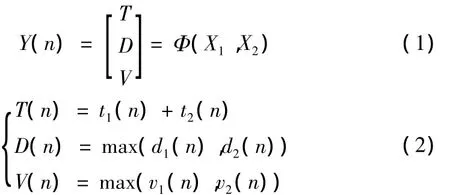
2 刀库及机械手多态分系统状态分析

2.1 多态分系统状态定义

储刀选刀分系统的性能参数为：时间t1、精度d1和振动v1，机械手换刀分系统的性能参数为：时间t2、精度d2和振动v2，不同换刀次数下的实际性能值可以通过可靠性试验配合综合性能测试获得。

设性能函数G(n)的分布范围是［gmin，gmax］，其中gmin是最好性能、gmax是最差性能：

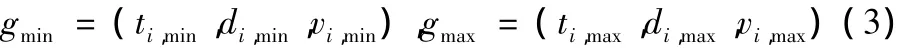
其中i=1，2，1为储刀换刀分系统、2为机械手换刀分系统。

将连续的性能函数离散化［7］，时间ti分成Mti个子区间 ［ti，max，ti，1)，［ti，1，ti，2)，…，［ti，Mti－1，ti，min］;精度di分成Mdi个子区间 ［di，max，di，1)，［di，1，di，2)，…，［di，Mti－1，di，min］;振动vi分成Mvi个子区间 ［vi，max，vi，1)，［vi，1，vi，2)，…，［vi，Mti－1，vi，min］，组成状态空间：

状态1工作时间最长、精度最差、振动最大，是最坏状态，表示性能失效，状态M表示最好、完备工作状态，状态M到状态1表示分系统性能逐渐退化的过程。

取各区间中值，可得分系统的各状态的性能值：Gi(n)={gi1，gi2，…，giM}

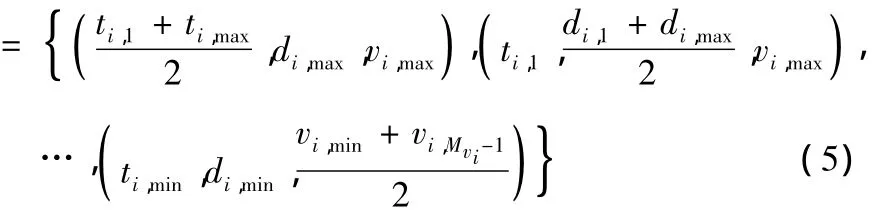
2.2 Markov方法的多态分系统状态概率计算

状态概率指在某一特定时刻系统处于各个状态的概率。通常定义为：

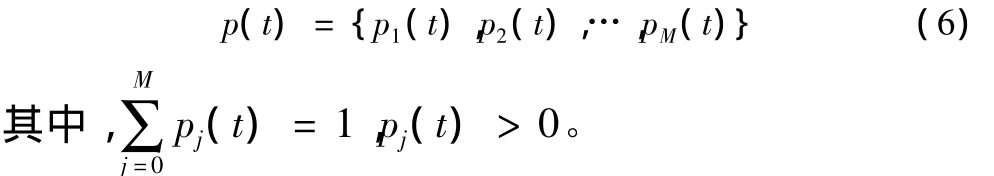
Markov链是Markov过程的一种，Markov过程主要是用于研究随机过程中状态与状态转移，是一种动态的描述，最基本的性质是无后效性［8］，简单表述为元部件或系统t时刻的性能状态仅仅与t－1时刻相关，与t－1之前都无关。对任意时刻t，状态x(t)取性能状态值gt的概率为：

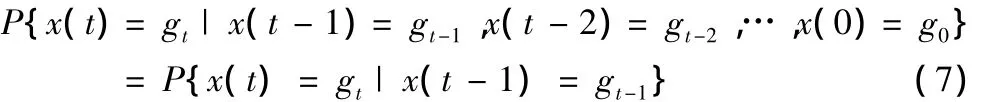
上述公式又可理解为在t－1时刻的性能状态值是gt－1的前提下，转移到时刻t时性能状态值为gt的概率。

分系统i的状态j的性能值为gi，j，其中i=1，2，j=1，2，…，Mi，对任意i，j，有gi，j+1≥gi，j，若分系统当前在状态j，故障事件使其从状态j转变为状态j－1，维修事件使其从状态j转变为状态j+1，Mi为最好状态，只能发生故障向状态Mi－1转变，1为最差状态，只能通过维修向状态2转变。失效时间及维修时间服从指数分布的分系统具有Markov随机过程特性，依据Markov转移概率的特点可以建立多态分系统i从性能状态ki到性能状态bi(ki，bi=1，…，Mi)之间的相关转移强度akjbj，并且这些转移都是由故障和维修引起的，若ki＜bi，akjbj=λkjbj，反之akjbj=μkjbj，一次转变只能在邻近状态之间发生，不考虑意外情况造成的突然失效，从而建立相关Markov模型，其中λkjbj为故障率，μkjbj为维修率，图2为刀库及机械手分系统i的Markov链模型。

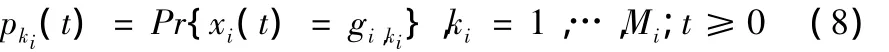
为求解该概率引用Trivedi提出的微分方程［9］：

初始条件为部件j处于最好状态，即pMj(0)=1，pMj－1(0)=…=p2j(0)=p1j(0)=0，由此微分方程组可求出pj(t)的解。

图2 分系统i的Markov链模型

采用上述方法可以建立刀库及机械手两分系统的Markov链模型并计算得出不同换刀次数下的状态概率pi1(n)，pi2(n)，…，piMi(n)，i=1，2。

3 UGF刀库及机械手多态系统可靠性建模

UGF通用生成函数法自上世纪八十年代提出以来，在多态系统可靠性分析上得到了广泛的应用。采用UGF进行可靠性分析时可以描述分系统i的性能状态分布［10］，即状态值gi，ki及其状态概率pki(t)，(i=1，2，ki=1，…，Mi)的关系，u1(z)为储刀选刀分系统的多态模型，u2(z)为机械手换刀分系统的多态模型：

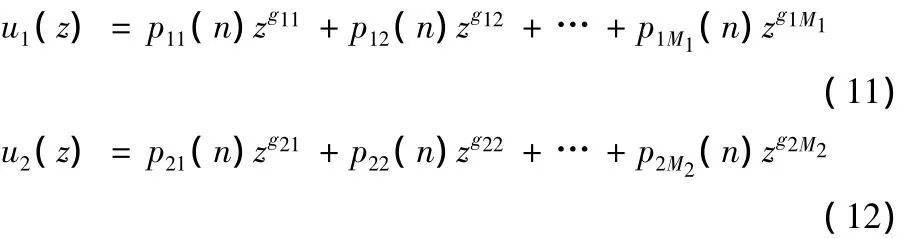
结合系统结构函数Φ可得刀库及机械手系统的通用生成函数为：

该式为刀库及机械手多态可靠性模型，表示系统各性能状态分布的情况，Z的指数为性能，Z的系数为各状态的概率，易于理解，计算时只需将分系统各个系数即状态概率分别相乘，Z的指数根据结构函数确定为性能状态向量第一项相加，第二、三项求最大值，注意利用：

合并同类项降低运算量。

4 刀库及机械手可靠性评估

若给定刀库及机械手可靠性性能指标的最小需求w=(T0，D0，V0)，便可估计出多态系统的性能可靠度为［11］：

式中，n为换刀次数，(Ts，Ds，Vs)为系统状态s的性能值，ps(t)为对应概率。刀库及机械手性能可靠度即取系统性能达到最小需求的状态的概率和。

5 实例分析

假设随着换刀次数的增加，储刀选刀分系统性能逐渐退化，根据测试数据，工作时间离散为7s、9s、11s，其中7s为最理想状态，11s超过技术指标需求;到位精度离散为3'、7'、41'，其中41'定义为精度超标失效;振动速度 2mm/s、3mm/s、4mm/s，其中 4mm/s振动太大失效，则状态定义为：

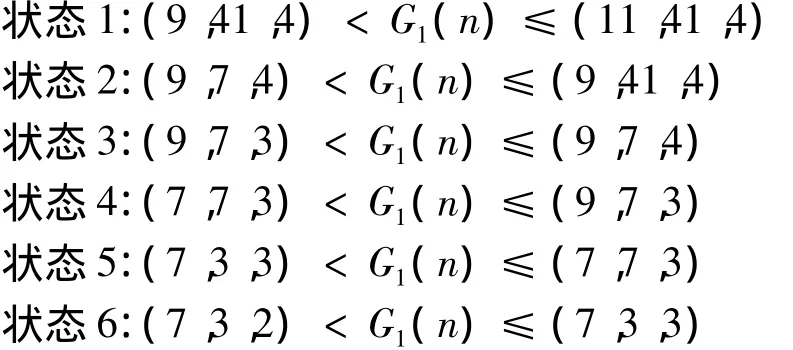
取区间中值，储刀换刀分系统的状态性能为：

其中初始条件为：

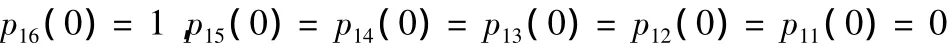
同理，可进行机械手换刀分系统的状态分析，综合可得系统Markov链模型如图3所示。

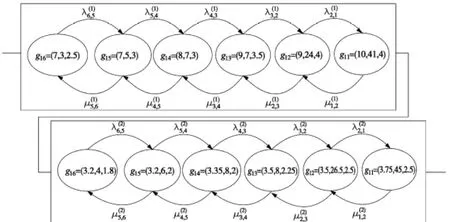
图3 系统的Markov链模型

用Matlab求微分方程数值解，取换刀次数为n=100000，可得：

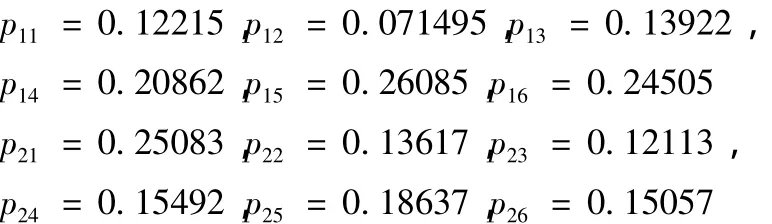
将状态及状态概率代入式(11)(12)，得系统换刀100000次时，分系统多态可靠性模型：

假设系统性能指标需求w=(12.5，24，4)，根据可靠度计算公式(14)得到刀库及机械手可靠度R(10000)=0.8978。

6 结束语

文中采用了Markov结合UGF的方法系统地给出了刀库及机械手的多态可靠性的建模及分析方法，真实地反映出效率、精度和平稳性性能的衰退对可靠性的影响，定量评估刀库及机械手在特定性能需求下的可靠性，弥补了传统二态可靠性分析的不足，部件与系统分开研究的方法更是降低了模型的复杂度和计算的繁复程度。

［1］张际良.多状态系统的性能可靠性［J］.自动化学报，1996，22(2)：246 －25.

［2］Barton R M，Damon W W.Reliability in a multi-state system.The Sixth Annual Southeastern Symposium on Systems Theory，Louisiana，USA，1974.

［3］Murchland J.Fundamental concepts and relations for reliability analysis of multi-state systems.Reliability and Fault Tree Analysis.Philadelphia：1975.

［4］杨建军，刘锋，黎放.多阶段任务多态系统可靠性建模与仿真［J］.火力与指挥控制，2011，36(2)：89－92.

［5］Lisnianski A.Extended block diagram method for a multistate system reliability assessment.Reliability Engineering＆System Safety，2007(92)：1601－1607.

［6］蒋仁言，左明健.可靠性模型与应用［M］.北京：机械工业出版社，1999.

［7］李春阳.基于多态系统理论的可靠性分析与优化设计方法研究［D］.长沙：国防科技大学，2010.

［8］马尔可夫链模型在空管自动化系统可靠性分析中的应用［J］.航空计算技术，2009(39)：15－21.

［9］Trivedi K.Probability and statistics with reliability，queuing and computer science applications.New York：Wiley;2002.

［10］安宗文.基于通用生成函数的离散化应力-强度干涉模型研究［D］.电子科技大学，2009.

［11］尚颜龙，蔡琦，赵新文，等.基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析［J］.核动力工程，2012，2，33(1)：117 －123.