联合整体和局部动态信息的空间桁架模型修正试验

侯吉林，欧进萍，2，Łukasz Jankowski

(1.大连理工大学 土木工程学院，大连 116024;2.哈尔滨工业大学 土木工程学院，哈尔滨 150090;3.波兰科学院基础技术研究所智能技术部，华沙 02-106，波兰)

结构健康监测是土木工程中的研究热点，模型修正是结构健康监测的重要理论基础部分，为结构的监测、预警和安全评定提供可靠的理论依据。随着土木工程中结构不断向大型化和复杂化发展，加上测试信息的有限性和不可避免的误差性，使得对复杂结构整体进行准确的模型修正越来越困难。因此如何对结构进行动力测试，并合理充分地利用实测信息，是进行准确模型修正的有效保证。

模态是结构最基本的动态信息，并且容易获取，在环境激励下也可以被识别，因此基于模态信息的损伤识别和模型修正方法被广泛应用于土木结构中。李辉等［1］对基于模态的结构动力模型修正方法进行了系统综述。赵建华等［2］通过计算结构损伤前后频率和振型的变化确定出构损伤位置和大小。韩东颖等［3］基于频率和当量损伤系数进行井架钢结构的损伤识别。施洲等［4］利用模态的摄动，在考虑边界条件变异的情况进行桥梁结构的损伤识别。模态是结构的基本参数，是不随激励而改变的。然而实际操作中能够识别出来的往往是少数几阶低阶模态，对局部的损伤也不敏感，一般用这些数据准确识别整体结构的所有参数还比较困难。

目前，子结构方法通过局部聚焦，对重要的局部构件，利用局部的动态响应进行修正，一定程度上避免了整体结构修正的困难。Reich和Park［5-6］把整体柔度分解成多个子结构的局部柔度或单元柔度，再由子结构柔度的变化定位损伤。Yang等［7］利用连续非线性最小二乘方法估计子结构的加速度、速度和位移以及刚度和阻尼等参数，同时估计整体结构对子结构边界的作用力，这种方法可以有效地追踪结构损伤随时间的变化。樊素英等［8］应用广义卡尔曼滤波，可得到两相邻单元的质量、刚度和阻尼等物理参数。Xing等［9］限定剪切模型中每个子结构的自由度数目后，通过交错子结构的方式由ARMAX方法识别结构损伤。Wang等［10］利用拟静力位移向量方法简化边界偶合力，然后由遗传算法识别子结构。欧进萍等［11］提出约束子结构方法，分别利用局部的响应构造独立的虚拟的约束子结构模型，实现将子结构从整体中分离出来，然后借用针对整体模型的经典方法进行子结构局部模型修正。子结构方法只能识别子结构的局部，而且一般需要监测或识别子结构的边界，当子结构的边界复杂时，方法应用会存在一定的困难。

综上，结构的整体试验一般不容易捕捉到局部误差信息，而局部动态测试也不能反应结构整体参数。特别是类似桁架这样的结构，桁架往往由成百上千个杆件组成，每个杆件的变化或者损伤对整体桁架结构的影响很小。为了同时修正结构整体参数和局部误差，本文联合所有结构整体和局部的动态信息，对桁架结构进行精细模型修正。

1 模型修正方法

结构模型修正方法是将实测的结构动态信息作为已知条件，选取合适的物理参数，然后将试验模型和理论有限元模型之间误差范数作为目标函数，对参数进行优化，使目标函数达到最小。实测动态信息的准确性及数据量是进行结构准确模型修正的关键。结构的模态(频率和振型)是模型修正中常利用的动态信息，频率识别精度高，但是频率一般对局部参数变化不敏感。虽然振型对局部变化相对敏感，但是振型识别的误差比较大。本文针对空间桁架结构的特点，为了获得结构全面的反映结构整体和局部的动态信息，分别对结构进行整体模态测试和大量的局部杆件动态测试，在保证整体低阶模态一致的情况下，尽量充分挖掘对局部杆件敏感的动态信息，联合整体和局部的动态信息建立的目标函数，见式(1)，然后目标函数(1)进行桁架结构的模型修正。因为振型识别的误差往往较大，所以式(1)中只利用结构的频率信息，详细的内容会在试验中介绍。

2 桁架试验

本节通过空间桁架模型的试验，介绍联合整体和局部动态信息的模型修正方法，并验证方法的有效性。

2.1 桁架模型

二十跨空间桁架，如图1所示，两端支座铰接，右端可滑动，总长8 m，高0.9 m，宽0.56 m，一共108个结点，312个杆件。钢材的弹性模量2.06 GPa，密度7 850 kg/m3。空间桁架由钢管通过球结点和螺栓组装而成，结点连接方式如图1右下角，球节点的直径为80 mm。杆件按照钢管的半径分为三种类型，见表1。

图1 桁架的试验模型Fig.1 A truss experimental model

表1 桁架结构中的三种杆件Tab.1 Three kinds of element in truss structure

2.2 桁架整体模态试验

在整体桁架底层的结点上布置加速度传感器［12］，如图2。采用多人用力锤在不同结点随机的敲击，敲击过程中结点位置不断随机地更换，这样做的目的是模拟环境激励。利用随机响应识别的振型和频率见图3和表2。

首先初步建立理论有限元模型，把每一个杆件简化为一个梁单元，则有限元模型包含108个节点，312个杆件，每个结点6个自由度，共638个自由度。单元截面面积和惯性矩由钢管的设计几何尺寸计算。有限元桁架模型的单元为刚接，并在模型的结点上考虑附加试验模型中球结点和螺栓的质量，结点质量初步估计为2.83 kg。图3和表2分别比较了试验模型和初步理论有限元模型(图3中理论模态为从图4中整体结构模态中提取的对应测点处模态)的振型和频率，可以看出，两者误差比较大，大约在30%左右。这说明初步建立的理论有限元模型误差较大，需要对其进行模型修正。

图2 整体加速度传感器布置图Fig.2 Accelerations placement

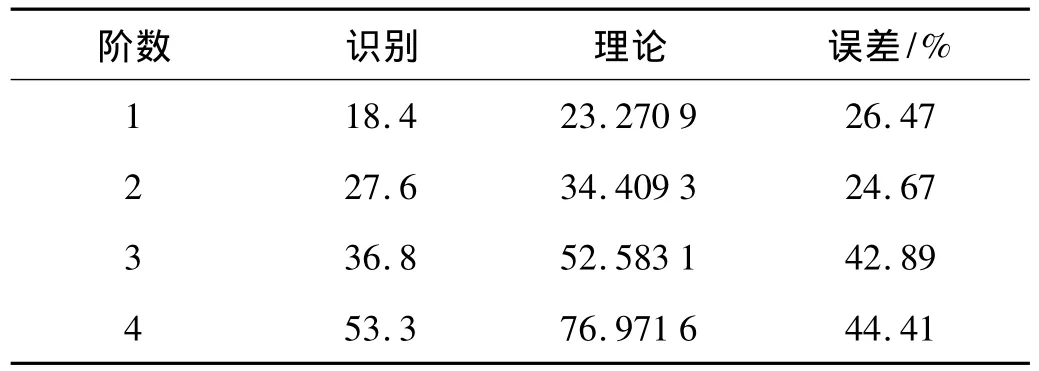
表2 整体的低阶频率Tab.2 The lower order natural frequencies of global structure

图3 整体模态比较Fig.3 The comparison of modes of global structure

图4 有限元模型的整体模态Fig.4 The global modes of FEM

2.3 局部动力测试

结构杆件的参数变化会引起结构动力特性(包括模态)的变化，模态的改变一般关于不同杆件的灵敏度是不同的。低阶模态一般关于整体结构中各个杆件的灵敏度都比较小，而且各个杆件的灵敏度往往相差不大;而高阶模态一般会对某个(或某些)局部杆件灵敏度比较大，并且各个杆件的灵敏度往往相差会比较大，换句话说，即这个高阶模态主要由某个(某些)局部杆件参数决定，其他杆件的参数的变化对这个高阶模态影响比较小。结构的测量响应或对应识别模态是反映整体信息，还是更多地反映局部动态信息，主要取决于激励和测试的位置。所以为了获得对局部灵敏度较高的高阶模态，进行局部测试试验，试验中在杆件中间附加质量，并激励其中间位置。

对桁架结构的主要杆件按照杆件的长度和位置分为4类，见图5，对这四类杆件进行局部动态测试。为了提高杆件的局部动态特性，在杆件的中间附加质量。由于加速度传感器和其连接件的质量为340 g，所以试验中通过在杆件上布置传感器可实现附件质量，并且能由所布传感器的数目调节附加质量的大小。对于较长的杆件，其相对局部刚度比较小，则附加一个质量即可;若杆件比较短，其相对局部刚度比较大，则需布置多个质量。四类杆件的传感器或附加质量的布置情况如图6所示。

图5 杆件的四种工况Fig.5 Four kinds of elements

图6 质量的布置情况Fig.6 The placements of additional masses

首先以一个竖面直杆为例，说明和试验验证附加质量可以提高桁架杆件的局部动态特性。在一个竖面直杆上分别布置两个、三个和四个质量块(传感器)，然后利用小锤敲击杆件的中间位置，测得其加速度时程，并对响应进行频谱分析，对应的三组功率谱如图7。由于是对杆件局部进行激励，因此必然会激励起杆件的局部模态。附加质量越大，则杆件的局部特性越明显。由图7可以看出，当布置两个或三个质量时，整体结构的响应功率谱含有多个峰值，很难判断出哪个频率属于杆件的局部频率，哪些反映结构的整体模态，因此局部动态特性不够明显;当布置4个质量时，其功率谱只有一个峰值，表明局部激励的能量绝大部分被局部杆件和附加质量所吸收，该振动为杆件按照局部频率振动。将这个频率定义为杆件的局部主频率，局部主频率主要与杆件的刚度有关。利用小锤在杆件上进行局部激励，当没有附加质量或者质量较少时，由于桁架杆件相对较轻，杆件振动能量相对较小，所以小锤激励的能量会分散到杆件的结点上，从而激励起更多整体模态的振动;当增加附加质量后(杆件的刚度是不变的)，附加质量会吸收激励的大部分质量，从而只有少量激励能量转移到结点。所以从能量的角度可以解释附加质量可以在一定程度上增加杆件的局部特性。

为比较实际杆件的局部主频率和理论模型的局部主频率，试验中分别在空间桁架结构的竖面斜杆中挑选14个杆件，在平面斜杆中挑选16个杆件，在平面直杆中挑选20个杆件，在竖面直杆中挑选8个杆件，对这58个杆件按照图6的方式布置传感器(质量)，并利用小锤进行局部激励，识别的杆件局部主频率如图8。为了方便比较，对每类杆件只需选取一个杆件进行比较，试验识别的局部主频率和理论计算的局部主频率分别见表3，可以看出两者误差较大，也说明相对于实际模型，初始理论有限元模型的误差较大，需要进行模型修正。

图7 功率谱Fig.7 The power spectrum

图8 局部主频率Fig.8 The local primary frequencies

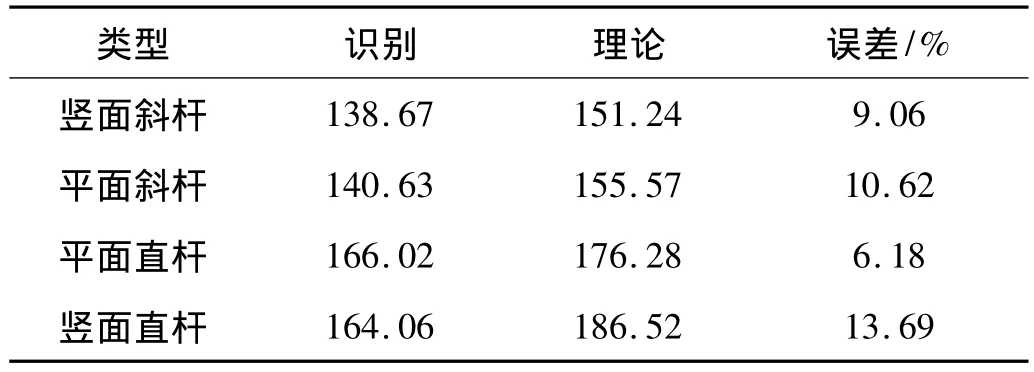
表3 杆件局部主频率的误差Tab.3 The errors of local primary frequencies of 4 kinds of elements

2.4 修正参数的选取

实际中，钢管的材料弹性模量、尺寸和密度的误差一般很小，故结点的误差是导致初步理论模型的结构低阶频率(表2)和局部主频率(表3)的误差的主要原因，因此模型修正中对结点进行修正。

首先针对试验桁架模型杆件结点连接的实际情况，同时考虑球结点、螺栓和钢管实际连接方式建立有限元模型。如图9所示，对杆件进行精细的建模，考虑球结点(半径r=4 cm)对杆件端部位置的局部加强，设强化刚度为k，参数k为球结点(r=4 cm)处刚度与钢管刚度的比值，具体k的大小需要进行优化;此外考虑螺栓连接引起的局部弱化，设弱化长度为l，螺栓弱化后刚度按照螺栓的实际尺寸进行计算，长度l需要进行优化。由于球结点打孔，并与各种螺栓和螺母相连接，其结点的实际质量m并不容易直接估计，故结点质量m需要修正。因此，模型修正中需要修正的参数有强化刚度k，弱化长度l和结点质量m。

图9 杆件的精细建模Fig.9 Fine modeling of the element

2.5 修正参数的选取

若根据图9所示对杆件进行精细建模，一个杆件划分为9个单元，包括两个球结点的强化单元，两个螺杆的弱化单元，中间钢管划分为5单元，则桁架重新建立模型后至少为2 606个结点，2 918个杆件，15 614个自由度，这显然使模型变得非常复杂，在模型计算分析中，大大增加计算量。因此，采用模型缩聚方法对杆件子结构缩聚建模。

首先按照图9，同时考虑杆件强化和弱化区域，建立杆件的刚度和质量矩阵，每个杆件含有9个单元，共60个自由度;然后将杆件的60个自由度，采用Guyan缩聚的方法缩聚到杆件两端结点的12个自由度上，缩聚后子结构的刚度矩阵和质量矩阵均为12维的方阵。最后再将缩聚后杆件的刚度和质量矩阵集装到整体结构。对于附加质量(传感器)的杆件，则直接将精细建模的杆件(60自由度)集装到整体有限元模型中，不进行模型缩聚。这样，在保证整体模型的自由度数的较少前提下，既能考虑杆件的实际连接方式，又能满足进行杆件局部动力分析的精度。

2.6 模型修正

利用图3中识别的4阶整体模态和图8中识别的58个局部主频率优化识别结点质量m，以及4类杆件的球结点强化刚度ki和螺栓连接长度为li(i=1，2，3，4)。利用目标函数(1)，由Matlab的fminsearch优化工具箱进行优化。

优化过程中涉及到实测模态匹配和理论局部主频率计算的问题。由于识别的图3中4阶整体模态不一定对应着结构有限元的前4阶模型，因此模态匹准确是准确模型修正的一个前提，本文利用振型的相关性(通过MAC值计算)判断实测4阶频率的归属。尽管图3中振型存在一定的误差，但是在优化的目标函数中(见式(1))并没有利用这4阶振型的数值信息，所以振型的少许误差不会影响模型修正的精度。关于理论局部主频率计算方法:一种方法是直接利用刚度和质量矩阵进行特征分解，分析各阶模态的局部特征来获得局部主频率，这种方法计算量大;第二种方法借鉴局部动力测试的试验方法，即在附加质量的桁架有限元模型的杆件中间施加脉冲响应，计算脉冲响应并进行傅里叶变换，然后利用峰值提取法由频率响应识别杆件的局部主频率。第二种方法快速直接，所以本文采用的第二种方法确定杆件的局部主频率。

可以获得球结点的优化质量为m=3.33 kg，球结点强化刚度和螺栓连接长度的优化参数见表4。将修正后的参数代入有限元模型中，理论有限元的整体结构频率和振型与试验识别值及二者间的误差分别见表5和图10。杆件的局部主频率的误差由于篇幅原因，这里不再一一列出，只挑选4个具有代表性的杆件的局部主频率，理论模型的频率和识别频率及其误差见表6。可以看出，所有误差中的最大值为5.55%，能满足精度要求，说明修正后的空间桁架模型与实际桁架结构无论是整体和局部都具有一致的动态特性，桁架模型得到有效和准确的修正。

表4 结点修正Tab.4 The model updating of the node parameters

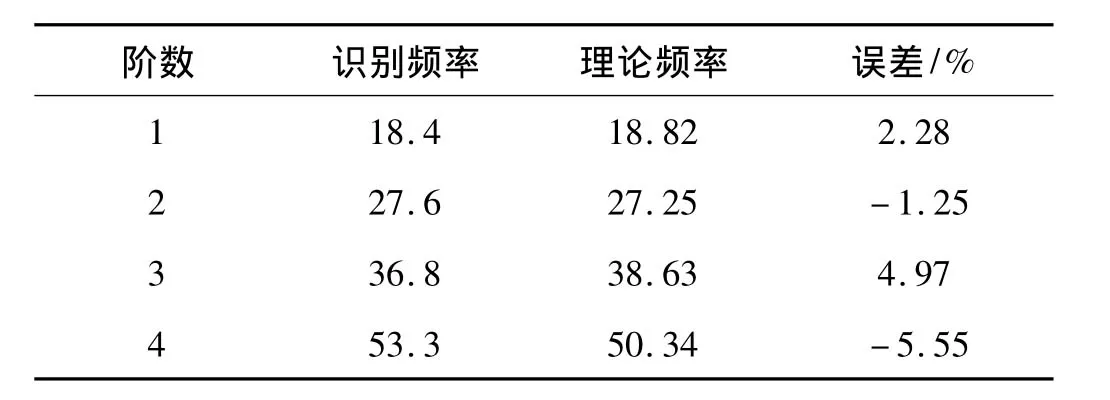
表5 整体低频频率Tab.5 The lower order natural frequencies of global structure

图10 整体模态比较Fig.10 The comparison of modes of global structure

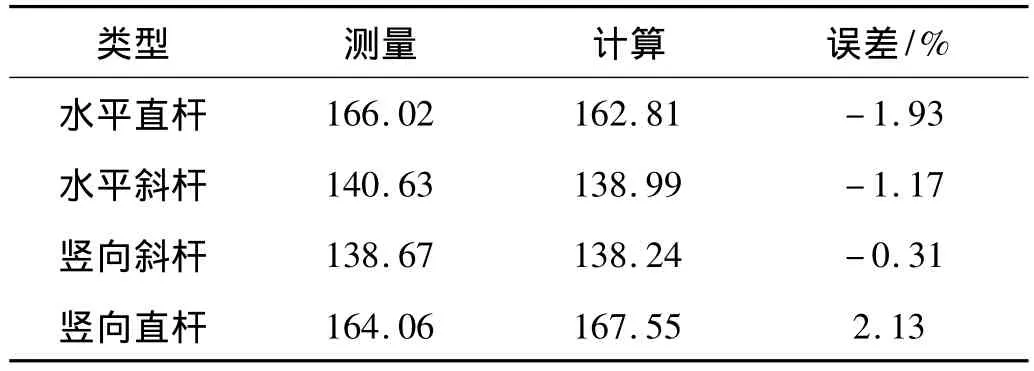
表6 杆件局部主频率的误差Tab.6 The errors of local primary frequencies

3 结论

本文有机地联合结构的整体和局部的动态信息，完成了空间桁架的模型修正试验，并得到了以下主要结论:

(1)针对空间桁架的特点，在局部杆件上附加质量可提高其局部的动态特性，使其在局部激励的作用下以局部主频率振动为主，有利于获得杆件的局部动态信息;

(2)局部主频率是主要反映局部特性的参数，低阶模态是主要反映整体结构特性的参数，因此联合二者，可充分的利用实测数据，有效实现结构的模型修正;

(3)先对局部杆件进行精细建模，使其满足局部动态特性的要求，然后对其进行模型缩聚，缩小自由度数目，使有限元模型在同时满足整体和局部动态特性的基础上，提高优化的计算效率。

［1］李 辉，丁 桦.结构动力模型修正方法研究进展［J］.力学进展，2005，35(2):170-180.

LI Hui，DING Hua.Progress in model updating for structural dynamics［J］.Advances In Mechanics，2005，35(2):170-180.

［2］赵建华，张 陵，相秉志，等.一种不完备测试数据下的结构损伤识别方法［J］.应用力学学报，2010(4):670-673.

ZHAO Jian-hua，ZHANG Ling，XIANG Bin-zhi，et al.A method for structural damage identification based on incomplete measured data［J］.Chinese Journal of Applied Mechanics，2010(4):670-673.

［3］韩东颖，时培明.基于频率和当量损伤系数的井架钢结构损伤识别［J］.工程力学，2011(9):109-114.

HAN Dong-yi， SHIPei-ming. Damageidentificationof derrick steel structures based on frequency and equivalent damage coefficient［J］.Engineering Mechanics，2011(9):109-114.

［4］施 洲，赵人达.基于模态参数考虑边界条件变异的桥梁结构损伤识别［J］.应用力学学报，2012(2):191-196.

SHI Zhou， ZHAO Ren-da. Damage detection of bridge structure accounting for boundary condition variation based on mode parameters［J］.Chinese Journal of Applied Mechanics，2012(2):191-196.

［5］Reich G W，Park K C.Experimental application of a structural health monitoring methodology［J］.S.C.Liu.Proceedings of SPIE，In Smart Structures and Materials，2000，(3988):143-153.

［6］Park K C，Reich G W，Alvin K F.Damage detection using localized flexibilities［M］.Structural Health Monitoring，Current Status and Perspectives，F.K.Chang，Technomic Publishers，1997:125-139.

［7］ Yang J，Huang H.Substructure damage identification using sequential nonlinear lse method，4th International Conference on Earthquake Engineering［C］.Taipei，Taiwan.October 12-13，2006，Paper No.119.

［8］樊素英，李忠献.桥梁结构物理参数识别的双单元子结构法［J］.工程力学，2007，24(6):68-72.

FAN Su-ying，LI Zhong-xian.A double-element substructure method for physicalparameter identification ofbridge structures［J］. Engineering Mechanics，2007，24(6):68-72.

［9］ Xing Z，Mita A.A substructure approach to local damage detection of shear structure［J］.Structural Control and Health Monitoring，2012，Doi:10.1002/stc.439.

［10］ Wang X J，Koh C G，Zhang Z.Damage identification based on strain and translational measurements with substructure approach［C］.First Middle East Conf.on Smart Monitoring，Assessment and Rehabilitation of Civil Structure，February 8-10，2011，Dubai，UAE.

［11］ Hou J，Jankowski L，Ou J.Experimental study of the substructure isolation method for local health monitoring［J］.Structural Control and Health Monitoring，2012，19(4):491-510.

［12］孙晓丹.结构健康监测的传感器测点优化与损伤识别［D］.哈尔滨:哈尔滨工业大学，2010.