冲击载荷下矿用移动式救生舱动态响应的数值模拟

李志强，白 博，谢青海，2，王志华，曹世昌

(1.太原理工大学 材料强度与结构冲击山西省重点实验室，太原 030024; 2.西山煤电(集团)有限责任公司，太原 030053;3.山西东昌实业有限公司，原平 034100)

矿用救生舱是煤矿发生矿难时为无法及时撤离的遇险矿工提供的避难场所，在国内外应用日趋广泛［1-2］。特别当煤矿井下发生瓦斯或煤尘爆炸时，会产生强大的冲击波作用在舱体上使其发生变形甚至失效，直接影响舱体内矿工的生命安全，因此舱体的抗爆炸冲击性能是设计救生舱时必须考虑的首要因素。只有舱体具有足够的强度和刚度抵抗爆炸时产生的强冲击波，才能确保其成为矿山遇险时矿工的“希望之舟”。

目前，关于救生舱的安全强度应遵照《煤矿井下紧急避险系统建设管理暂行规定》，规定中要求救生舱舱体抗冲击压力不低于2×0.3 MPa(2为安全系数)。评定救生舱的抗冲击性能主要采用实物试验和数值分析方法。至今，国内仅有重庆煤科总院能完成实体救生舱的模拟井下巷道瓦斯爆炸试验［3］，由于是实物破坏性试验，将会消耗大量的财力人力，因此数值模拟成为计算救生舱强度的有效方法。救生舱强度数值分析是一个复杂的流固耦合问题，涉及爆炸性气体的爆轰、爆炸冲击、固体结构的动态响应等学科，采用完全耦合方法来研究救生舱抗爆炸性能将变得更加困难。通常采用解耦法，基本思想是通过数值仿真模拟井下瓦斯煤尘爆炸在井巷中产生的爆炸冲击载荷，将该载荷作为救生舱结构动力响应分析的载荷条件。江丙友等［4］，穆勇［5］，王磊［6］，林柏泉等［7］，徐景德等［8］对井下巷道内瓦斯爆炸冲击波传播规律进行了缩比模型研究，研究表明爆炸冲击波超压随传播距离增加不断衰减，但衰减幅度较小，巷道壁面、障碍物存在增大了冲击波超压。王长江［9］，杨旭东等［10］，金亮亮等［11］采用不同作用载荷对救生舱的静强度、舱体单元的动强度以及加强肋进行了简要计算分析，给出了救生舱整体性能计算分析的基本步骤。事实上，救生舱的抗冲击性能与作用在舱体上的爆炸冲击波超压峰值和持续时间有直接关系，而超压峰值取决于瓦斯爆炸释放能量和爆距［12］。按照国家规定，本文对初始200 m3瓦斯-空气混合气体爆炸作用在距爆源100 m处的救生舱整体和局部动态响应进行数值模拟。

1 有限元模型的建立

1.1 三维几何模型的建立

救生舱采用组合分体式，由过渡舱、生存舱和设备舱三部分组成，舱体之间采用法兰连接。每节舱体为12 mm厚的梯形波纹板，宽1 450 mm，长800 mm，高1 850 mm。利用Solidworks 2010建立了救生舱的三维几何模型，如图1所示。

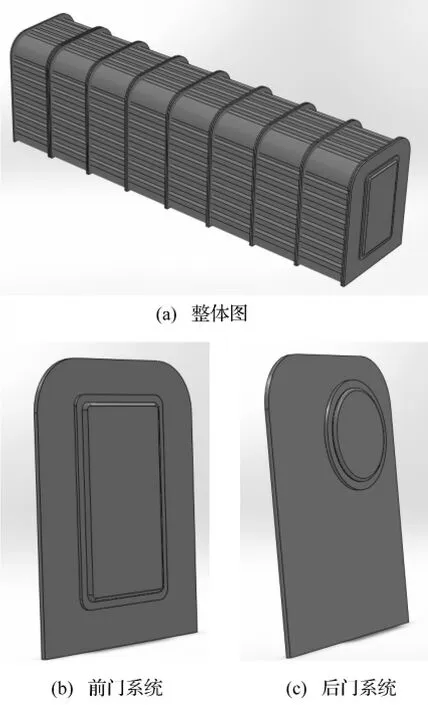
图1 救生舱三维模型Fig.1 3D model of chamber

1.2 有限元网格划分

网格划分的质量直接影响计算分析结果的精确性。由于救身舱结构比较复杂，部件繁多且尺寸相差较大，为了保证网格质量，对其进行以下简化:① 舱体外壳的厚度较其它两个方向尺寸相差很大，故将其简化为壳单元;② 认为连接法兰的螺栓强度足够，每节舱体的法兰采用理想接触，并忽略螺栓。

救生舱的三维几何模型导入ABAQUS软件CAE模块，根据上述有限元模型简化原则，对其进行网格划分，如图2所示。系统中各部件的单元类型、单元形状、几何特性、单元总数和节点总数列于表1。

图2 救生舱有限元网格Fig.2 Finite element mesh of chamber

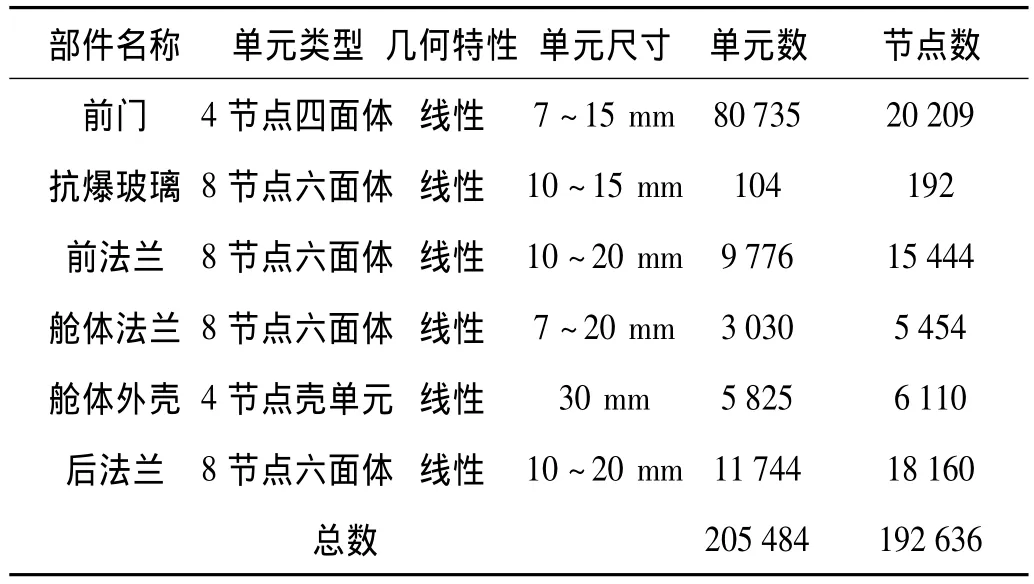
表1 各部件的有限元参数Tab.1 Finite element parameters of each part

1.3 材料模型

救生舱主体结构的材料为Q345，其中前后门为QT450-10，以及前门窗口为抗爆玻璃。其中，Q345和QT450-10选择非线性弹塑性本构模型，抗爆玻璃为脆性材料选择线弹性本构模型，主要力学参数列于表2。抗爆玻璃和未达到屈服强度的金属是线弹性的，为了描述材料的塑性特征，在ABAQUS中需要输入材料的强化曲线。强化曲线为真实应力-塑性应变曲线，可以通过名义应力-名义应变曲线转化得到。真实应变与名义应变的转化公式为:

真实应力与名义应力和应变的关系为:

塑性应变为:

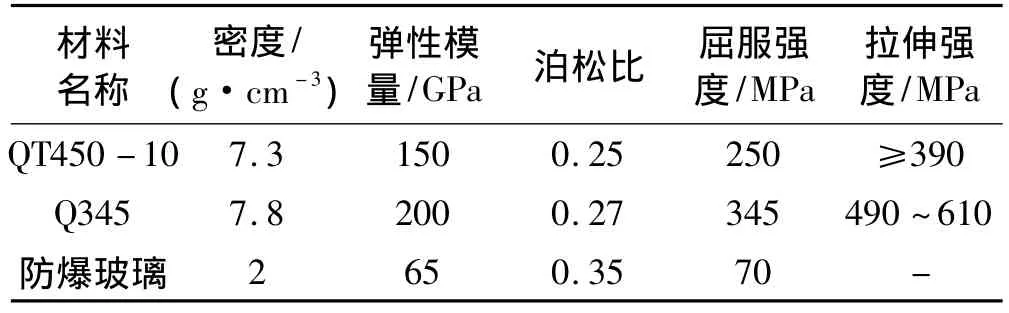
表2 材料的力学参数Tab.2 Material mechanics parameters

为了有足够的安全裕度，金属材料的破坏强度取其最小的拉伸强度，抗爆玻璃的破坏强度取其屈服强度。

1.4 边界条件与作用载荷

在数值模拟中，边界条件和作用载荷的确定是十分重要的，直接影响模拟结果的准确性。考虑到爆炸实际情况，舱体正面(门朝前)、后面、2个侧面和顶面受冲击载荷作用，底面为简支约束。由于压力峰值与爆炸冲击波作用的角度有关，在2个侧面和顶面作用的载荷强度是前后面的二分之一。本文首先按照国家对救生舱最低抗冲击波压力要求，采用峰值为0.6 MPa、历时600 ms的等效三角形压力波模拟冲击波对该舱的作用，如图3所示。然后保持载荷持续时间不变，增加峰值压力以期确定舱体的最大抗冲击载荷。

图3 等效三角形冲击波Fig.3 Equivalent triangular shock wave

2 计算结果与分析

采用ABAQUS动态显式算法，对上述工况进行计算，物理模拟时间为800 ms。国家暂行规定，舱体整体结构的最大等效应力不超过材料的破坏强度，最大变形不超过20 mm，同时要求舱体重点部位的最大等效应力不超过材料的屈服强度，最大变形不超过10 mm，这样才可以认为救生舱不会发生破坏和失效。下面重点给出和分析图3载荷下的计算结果。

2.1 救生舱整体结构响应计算结果及分析

2.1.1 应力结果

等效应力是衡量材料是否失效和破坏的重要依据，应力达到最大值时救生舱整体的等效应力云图，如图4所示。从图4可以看出，救生舱等效应力最大值出现在300 ms时，可达429 MPa。

图5给出等效应力最大处的应力-时间曲线。整个救生舱的最大等效应力出现在底面钢板和侧面法兰连接处，并且舱体中部侧面法兰应力值也较大，在这些部位可能出现屈服，进入塑性阶段，但不会发生破坏。

2.1.2 应变结果

图4 救生舱整体应力分布Fig.4 Overall stress distribution of chamber

图5 等效应力最大处的应力-时间曲线Fig.5 Stress history curve at the location of maximum effective stress

救生舱的最大等效塑性应变开始出现在320 ms时，此时的应变云图如图6所示。可以看出，整个结构有很少的单元发生屈服，应变最大值出现在侧面法兰和底面钢板的连接处，最大等效塑性应变可达0.0044。

图6 救生舱整体的等效塑性应变分布Fig.6 Overall effective plastic strain distribution of chamber

图7 应变最大处的应变-时间曲线Fig.7 Strain history curve at the location of maximum strain

图7给出等效塑性应变最大值处的应变-时间曲线，可以看出，在180 ms前没有塑性应变，即在弹性范围内;在320 ms时塑性应变达到最大值。

2.1.3 位移结果

在300 ms时刻整体结构变形最大，最大位移出现在中间一节舱体的侧面波纹板中央，最大位移为12.6 mm。此时，救生舱整体的变形分布如图8所示。同时，给出了位移最大处的位移时程曲线，如图9所示。可以看出，在300 ms时位移达到最大值，随后有明显的回弹。冲击波作用后(即600 ms后)，该位置的残余位移大约为2 mm。

图8 救生舱整体的变形分布Fig.8 Overall displacement distribution of chamber

图9 位移最大处的位移-时间曲线Fig.9 Displacement history curve at the location of maximum displacement

2.2 救生舱门系统的计算结果及分析

由于受冲击波正面作用，前后门系统所受载荷较大，为有限元分析的重点部位。门系统结构复杂(含门扇、门框、门闩、门轴、手柄或手轮等部件)，为了保证其密封性，需要有更高的刚度。在峰值为0.6 MPa的冲击波作用下，救生舱前后门系统的等效应力、塑性应变和位移的计算结果如图10～12所示。

图10 前后门系统的应力云图Fig.10 Stress contour of front and back door system

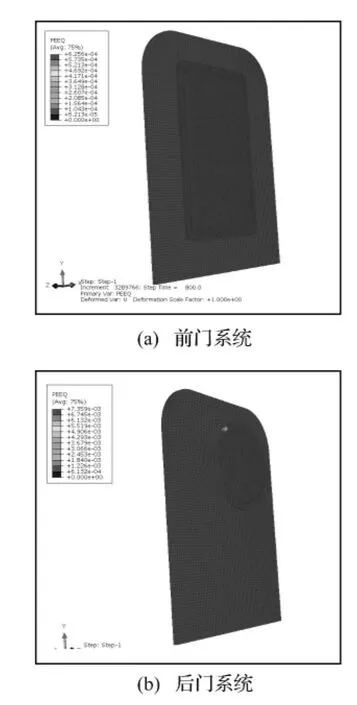
图11 前后门系统的塑性应变云图Fig.11 Plastic strain contour of front and back door system

图12 前后门系统的位移云图Fig.12 Displacement contour of front and back door system

在整个冲击过程中，前后门的最大应力值出现在300 ms时，如图10所示。可以看出，前后门的应力最大值分别为254 MPa和273 MPa，略高于屈服强度。但是，最大应力值出现在应力集中的部位，实际上，该应力集中对结构不造成破坏。

前后门系统最后时刻的等效塑性应变如图11所示。从图中可以看出，前后门系统的最大塑性应变值分别为0.000 6和0.007 4，并且仅仅出现在应力集中部位，而其它绝大部分区域在弹性范围内。

前后门系统的位移最大值也出现在300 ms时，如图12所示。前后门系统的最大位移分别为6.1 mm和8.5 mm，但是在最后时刻的最大残余位移仅仅为0.04 mm和0.22 mm，完全可以保证前后门系统的密封性要求。

2.3 救生舱的抗冲击性能研究

为了进一步研究救生舱的抗冲击性能，有限元计算了不同冲击强度下救生舱的结构响应。通过比较不同强度冲击波作用下的最大等效应力和位移，研究了救生舱在较大冲击载荷作用下的失效和变形程度。应力和位移的最大值通常出现在300 ms时，图13和14分别给出不同载荷作用下该时刻的最大应力和位移。可以看出，最大应力和位移随冲击波峰值压力的增大而近似线性增大。当超压峰值为0.72 MPa时，最大应力值接近材料的强度极限490 MPa，舱体不会发生破坏失效。此时，最大位移为18.8 mm，符合国家对舱体变形的要求。由此可知，该型号救生舱可确保在峰值为0.72 MPa冲击波的作用下舱体结构无破坏和变形失效。在更强冲击波作用下的计算结果为预测特大瓦斯爆炸中救生舱的损伤程度提供了依据。

图13 最大应力随超压峰值变化曲线Fig.13 Variation of maximum effective stress with peak overpressure

3 结论

图14 最大位移随超压峰值变化曲线Fig.14 Variation of maximum displacement with peak overpressure

应用Abaqus软件的动态显式算法分析了救生舱在不同强度冲击载荷作用下舱体的变形和应力分布情况。由于应力集中，最大应力和应变发生在法兰与底板的连接处，该位置容易出现屈服。最大位移出现在舱体侧面中心部位。该型号救生舱在峰值压力0.72 MPa的冲击载荷作用下保证舱体结构满足国家相关的破坏和失效要求，高于国家要求的最低抗爆压力(0.6 MPa)。

瓦斯爆炸产生的爆炸冲击波非常复杂，与救生舱外表面形状和约束方式有关，冲击波峰值和持续时间对舱体抗爆炸冲击性能影响很大，若将冲击持续时间减小到5 ms，舱体正面抗冲击峰值压力可达到2 MPa，但与煤矿井下瓦斯爆炸实际时间相差很大。为此，采用流固耦合方法计算作用在真实舱体上不同区域的爆炸冲击波，为舱体强度分析提供准确的载荷条件是非常必要的。

［1］汪 声，金龙哲，栗 婧.国外矿用应急救生舱技术现状［J］.中国安全生产科学技术，2010，6(4):119-123.

WANG Sheng，JIN Long-zhe LI Jing.The present status of overseas mine emergency refuge chamber technology［J］.Journal of Safety Science and Technology，2010，6(4):119-123.

［2］艾长波.矿用救生舱国内外发展概况［J］.舰船防化，2010，6:5-8.

AI Chang-bo.Research and application status of mine refuge chamber in china and abroad［J］.Chemical Defence on Ships，2010，6:5-8.

［3］樊小涛.矿用救生舱抗爆性能试验研究［J］.矿业安全与环保，2010，37(3):25-30.

FAN Xiao-tao.Experimental study of anti-explosion of movable mine rescue chamber［J］.Mining Safety and Environmental Protection，2010，37(3):25-30.

［4］江丙友，林柏泉，朱传杰，等.瓦斯爆炸冲击波在并联巷道中传播特性的数值模拟［J］.燃烧科学与技术，2011，17(3):250-254.

JIANG Bin-you，LIN Bai-quan，ZHU Chuan-jie，etal.Numerical simulation on shock wave propagation characteristics of gas explosion in parallel roadway［J］.Journal ofCombustion Scienceand Technology， 2011，17(3):250-254.

［5］穆 勇.瓦斯爆炸冲击波在掘进巷道传播的数值模拟［J］.煤炭技术，2008，27(6):92-94.

MU Yong.Numerical simulation of gas explosive shock wave in excavation roadway［J］.Coal Technology，2008，27(6):92-94.

［6］王 磊.瓦斯爆炸数值模拟研究［J］.矿业安全与环保，2009，36:23-25.

WANG Lei.Numerical simulation of gas explosion［J］.Mining Safety and Environmental Protection，2009，36:23-25.

［7］林柏泉，周世宁，张仁贵.障碍物对瓦斯爆炸过程中火焰和爆炸波的影响［J］.中国矿业大学学报，1999，28(2):104-107.

LIN Bai-quan，ZHOU Shi-ning，ZHANG Ren-gui.Influence of barriers on flame transmission and explosion wave in gas explosion［J］.Journal of China University of Mining ＆Technology，1999，28(2):104-107.

［8］徐景德.矿井瓦斯爆炸冲击波传播规律及影响因素的研究［D］.徐州:中国矿业大学，2002.

［9］王长江.基于LS-DYNA矿用救生舱抗爆性能的仿真分析［J］.科技视野，2012，1:46-47.

WANG Chang-jiang.Anti-explosion simulation and analysis of coal mine rescue capsule based on LS-DYNA［J］.Science ＆Technology View，2012，1:46-47.

［10］杨旭东，金亮亮，李家春.煤矿救生舱的爆炸模拟分析［J］.煤矿机械，2012，33(2):113-114.

YANG Xu-dong，JIN Liang-liang，LI Jia-chun.Explosion simulation and analysis of coal mine rescue capsule［J］.Coal Mine Machinery，2012，33(2):113-114.

［11］金亮亮，杨旭东，罗德刚.煤矿救生舱加强肋的设计与分析［J］.煤矿机械，2011，32(11):12-13.

JING Liang-liang，YANG Xu-dong，LUO De-gang.Design and analysis on stiffeners of coal mine rescue capsules［J］.Coal Mine Machinery，2011，32(11):12-13.

［12］李翼祺，马素贞.爆炸力学［M］.北京:科学出版社，1992.