一种提高平稳随机载荷识别精度的方法

廖 俊，蒋炳炎，时 伟

(1.中南大学 机电工程学院，长沙 410083;2.中南大学 航空航天学院，长沙 410083)

动态载荷识别是动力学中两大反问题之一，其中一类是系统辨识［1］，也就是已知响应和激励辨识出系统，对线性系统的辨识已经有了成熟的发展。而另一大类反问题就是载荷识别的问题，他是在已知系统特性和动态响应的情况下，对激励进行识别的方法。其解决方法大致可以分为频域方法和时域方法两类。本文介绍的加权平均算法是属于频域方法。动态载荷识别的频域法发展较早，是比较成熟的识别方法，并取得了很大进展。该方法的基本思想是在频域内建立系统的频率响应函数模型，再通过系统的输出识别出动态输入。由于振动系统在频域内其数学模型的输入输出关系为线性算子，因此、其线性算子的逆运算易处理。频域法的优点是其动态标定简单、识别精度较高。但存在频响函数矩阵H在共振区为病态，数值精度和稳定性等问题。

载荷识别最早因为航空领域飞机设计中为获得航空复合材料受力情况，以提高飞机飞行性能而被提出。Barlett等［2］对直升飞机的主轴所受到的动态力进行了识别，用的是频域方法，并采用的是加速度的响应数据进行识别，其识别效果一般。Giansante等［3］对 AH-1G直升机的尾部螺旋桨和主轴受到的随机外力进行了识别，他们用的也是加速度的响应数据，以及实测的传递矩阵在频域内进行辨识，验证了方法的正确性，并解决了识别过程中的轻度非线性问题，由于采用的实测频响函数，效果除了固有频率处有较大误差，其他地方精度尚可。Hillary等［4］用两个具有相同频率但是不同幅值的简谐力进行激励，对一个悬臂梁进行了载荷识别，发现影响识别精度的主要原因为响应的测量噪声，随后，他们系统的建立了载荷识别的频域方法，并在复杂的发动机叶片上进行了载荷识别，并指出因为加速度传感器对低频的不敏感，如果在低频采用应变计来测量响应效果要比用加速度计测量响应加速度的识别结果要好。孔炜等［5］用动态载荷识别频域法对火箭发动机推力偏心试验装置作研究。并对火箭发动机推力偏心载荷识别，其精度尚可，但只是一个自由度的识别。顾慧芝等［6］提出了一种用于识别未知作用位置的动态载荷方法——等效点动标定法，用频域法对飞机全动式平尾翼面抖振载荷的识别问题，他们的结论是恰当地选取标定点，这种方法可有效地识别出作用于结构上的外载荷的合力大小和作用位置。林家浩等［12-16］发展了逆虚拟激励法，提高了识别的效率。吴大宏等［7］用神经网络的方法对混泥土桥梁的载荷进行了识别，其计算效率不高，需要大量的样本。黄林等［8］利用小波分析在移动态载荷识别取得较好的效果。严刚等［9］对飞机上加筋复合材料结构的冲击载荷采用时域方法进行了识别研究工作，其识别结果非常好，但未对多点随机激励进行识别。朱斯岩等［10］用频域校正的方法对运载火箭动态载荷识别取得了较好的效果。姜金辉等［11］在基于谱分解的方法对随机载荷识别做了研究并进行了试验验证，对于改善病态有一定效果。近年来对载荷识别的研究逐渐开始热起来，如神经网络，小波变换等方法也引进来进行载荷识别的研究。

1 理论部分

1.1 假设条件

对于考虑到单自由度系统载荷识别仅需要进行简单标定即可以求出，本文所指载荷识别问题的研究都是在多自由度系统上进行，并采用多入多出的方式，同时识别多个点的激励载荷，且做出如下假设:① 载荷的位置是已知的且为固定不移动的;② 响应全部由待识别的载荷所产生，而不存在其他未知类型的激励形式作用于系统;③ 载荷作用的结构为线性结构。

1.2 矩阵直接求逆法

设线性结构在平稳随机激励作用下的运动方程为:

式中:M，C，K分别为线性系统结构的质量矩阵、阻尼矩阵和刚度矩阵，其维数为n×n，F为激励力，y为各自由度位移向量。

根据线性随机系统的响应功率谱求解公式:

由上式进行简单的矩阵变换可以得到:

上式就是在频域内进行载荷识别的基本算式。他由响应的功率谱密度函数和频率响应函数的广义逆求得激励的功率谱密度函数。其中上标“+”表示对指定矩阵求广义逆。“T”表示转置，“*”表示共轭。一般来说载荷识别中的频响函数H不为方阵，其求逆过程只能是求广义逆。且式(3)直接求解对于多自由度结构其求解过程计算量效果很差，识别结果容易受到噪声干扰而使得误差放大。

1.3 逆虚拟激励法［12－16］

设对于多点激励的响应功率谱矩阵为Syy，根据线性结构的特点，如果激励具有相干特性，那么响应也具有相干性。对响应功率谱矩阵可进行特征值分解:

其中:λ为响应功率谱矩阵Syy的特征值，ψ为响应功率谱矩阵Syy的特征向量，“H”表示共轭转置。其中的r为响应功率谱矩阵Syy的秩。

对于激励为完全相干情况［11］:其响应功率谱矩阵与激励的功率谱矩阵的秩为1;对于激励部分相干情况下其响应功率谱矩阵的秩1＜r＜m，其中m为激励响应功率谱矩阵的维数;对于激励为完全不相干情况下，其响应的功率谱矩阵的秩为m。

因此对于任意相干问题，上述特征值问题解答可以用QR正交分解的方法进行。具体的QR正交分法求矩阵特征值问题这里不做详述，可以从矩阵分析等基础教材［17］中得到。

由于实际系统的功率谱矩阵都应为非负定的，其所有的特征值也应当为非负的。即有λj＞0，(j=1，2，…，r)。

设:

则响应的功率谱矩阵可分解成如下的形式:

根据逆虚拟激励法［12］构造虚拟响应:

反演计算得到虚拟激励:

经过如下的演算即可得到所求的激励功率谱矩阵:

其中:

如果识别系统的自由度较小，在几10到几100之间，则可用上述方法进行载荷识别，如果自由度数更多的情况，可适当采用对识别系统进行振型叠加法以提高计算效率。

1.4 加权平均算法

矩阵条件数可以给出一种粗略的衡量尺度，反映方程组Ax=b中系数矩阵和常数项中的元素的误差对方程解x的影响程度。本文利用这一特点发展条件加权平均算法来提高载荷识别的精度。

矩阵条件数定义为:

根据逆虚拟激励法，虚拟激励由如下式子求得:

其中的H(m×l)为频率响应函数，要求m≥l。将上式中的频响函数写成行向量组成的矩阵［18］:

其中:r为 Syy的秩，Ri(i=1，2，…，m)为矩阵 H 的行向量。

将频响函数矩阵H中的任意l行组成l×l的阵Hi(i=1，2，…，k)，同时选取对应的l个虚拟响应构成新的虚拟响应向量(i=1，2，…，k)，求得其虚拟激:励

设方阵Hi的条件数为:

定义一个阈值b为:

定义权重为:

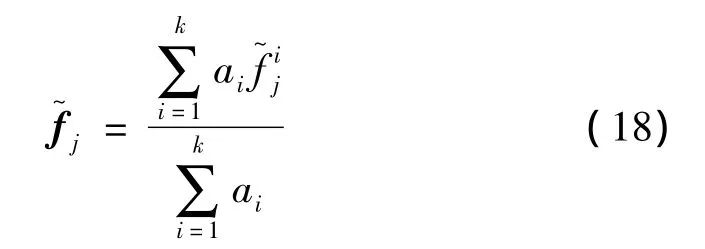
算法通过矩阵条件数的大小剔除引起病态的条件数较大的矩阵分量，达到抑制求逆过程中矩阵病态对识别精度的影响。

再将式(18)代入(8)即可以求得所需的激励功率谱密度函数。

2 仿真分析

建立如下图1所示的一个9自由度模型。设在m2和m4两处受到了平稳随机激励力的作用。

具体的激励力功率谱矩阵表达式为:

图1 9自由度剪切模型Fig.1 A 9 DOF shear type model

其中:S1为m2处的平稳随机水平激励力，其自功率谱密度函数为梯形曲线如图2中理论值所示曲线;S2为m4处的水平激励力的自功率谱密度函数，为梯形曲线如图3中理论值所示曲线;两个激励力的互相干系数为ρ，迟滞时间差为Δt。

设 ρ=0.7，Δt=0.08。阻尼比0.02，将频率范围设定为(18～1 000 rad/s)，设频率步长0.1 rad/s。1%的随机噪声加入到响应功率谱中用于模拟测量环境噪声。仿真过程选择测点(3，5，7)识别激励点(2，4)。先计算出响应的功率谱密度值，用本文提出的条件数加权算法进行载荷识别，并与直接求逆的常规方法进行对比，常规求广义逆的算法见公式(3)。仿真结果如图2到图9所示，其中图2、图3、图6、图7是分别为用条件数加权算法计算的S1自谱、S2自谱、互谱的实部和虚部;与之相比较，图4、图5、图8、图9则是用常规的矩阵直接求逆方法计算的对应的载荷功率谱值。表1为条件数加权算法与直接求逆方法的计算误差的比较。

表1 两种算法反演误差比较Tab.1 Comparison of error of two algorithms

图2 加权平均法识别自谱S1Fig.2 Identification result of S1 by weighted average method

图3 加权平均法识别自谱S2Fig.3 Identification result of S2 by weighted average method

图4 直接求逆识别自谱S1Fig.4 Identification result of S1 by direct inversion method

图5 直接求逆识别自谱S2Fig.5 Identification result of S2 by direct inversion method

图6 加权平均识别互谱实部(S12)Fig.6 Identification result of real part of S12 by weighted average method

图7 加权平均识别互谱虚部(S12)Fig.7 Identification result of imaginary part of S12 by weighted average method

图8 直接求逆识别加权平均识别互谱实部(S12)Fig.8 Identification result of real part of S12 by direct inversion method

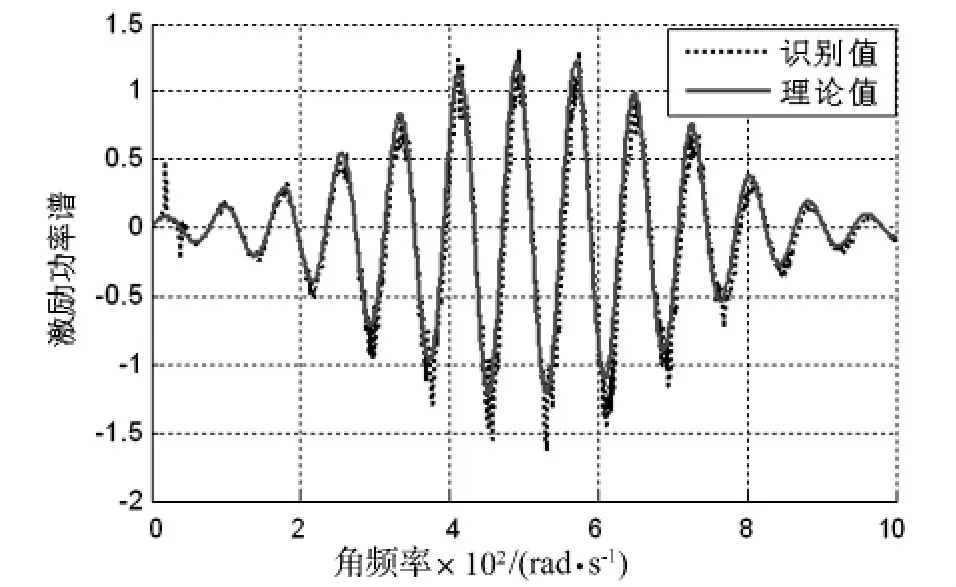
图9 直接求逆识别加权平均识别互谱虚部(S12)Fig.9 Identification result of imaginary part of S12 by direct inversion method

从图2到图9可看出，在共振频率(第3阶和第4阶)附近用直接求逆的方法计算的结果出现了较大的跳动，加权平均算法有效的改善了精度，识别结果明显要好于直接求逆方法。表格1同样说明本文提出的方法对于识别精度的提高有明显的作用。仿真表明方法在一定程度上能改善识别的精度。但算法并不能消除环境噪声，测量精度所带来的误差，尤其是在测点选择不当的情况下。且算法在反演过程中需多次求逆，会给计算带来负担，因此算法在提高精度的同时是以牺牲计算时间为低价的，但结合逆虚拟激励法的高效特点，对于一般载荷识别计算是可以接受的。

3 试验验证

试验在100 cm×60 cm×1.0 cm铝蜂窝板上进行，且将板的一端进行固定。在T1，T2处加载不相干的两个平稳随机激励力如图10所示。两个不同的信号发生器用来产生不相干的平稳随机激励信号，其中一个为DH1301信号发生器;另一个为Agilent 33250A信号发生器，他们都通过功率放大器DH5871驱动到两个JZQ-50电磁激振器，将力作用在T1，T2。并用BISEL力传感器记录力的时程数据。在A3～A8布置有前一个试验同类型的加速度传感器测量响应加速度，参数如表2所示。

图10 铝板与传感器布局Fig.10 Aluminum sheet and the sensor placement

表2 加速度传感器标度Tab.2 Scale of acceleration transducer

测得试验数据后，分别用(A5，A7，A8)和(A4，A7，A8)两组测点识别T1，T2两处激励力。两组测点组成的频响函数条件数随频率变化曲线如图11所示。

图11 测点组合(A5，A7，A8)与(A4，A7，A8)的条件数对比Fig.11 Comparison of condition number between(A5，A7，A8)and(A4，A7，A8)

测点组合(A5，A7，A8)条件数在各频道都明显小于测点组合(A4，A7，A8)，因此可以预测(A5，A7，A8)的识别结果将好于(A4，A7，A8)。

图12为用条件数加权方法与常规方法以响应测点组合(A5，A7，A8)识别激励力T1自谱的结果。图13为用条件数加权方法与常规方法以响应测点组合(A5，A7，A8)识别激励力T2自谱的结果。图14为用条件数加权方法与常规方法以响应测点组合(A4，A7，A8)识别激励力T1自谱的结果。图15为用条件数加权方法与常规方法以响应测点组合(A4，A7，A8)识别激励力T2自谱的结果。

图12～图15表明测点组合(A5，A7，A8)识别结果优于组合(A4，A7，A8)，验证了预测;同时，两组组合情况条件加权方法计算结果均优于常规算法，显示出算法对于改善识别结果的有效性。

图12 用响应点(A5，A7，A8)识别T1自谱Fig.12 Identification of T1 Auto-PSD using(A5，A7，A8)

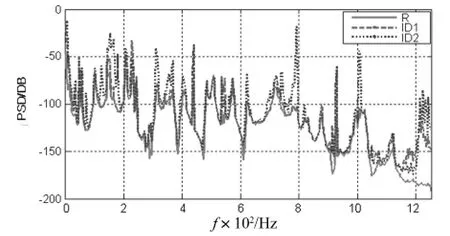
图13 用响应点(A5，A7，A8)识别的T2自谱Fig.13 Identification of T2 Auto-PSD at(A5，A7，A8)

图14 用响应点(A4，A7，A8)识别T1自谱Fig.14 Identification of T1 Auto-PSD at(A4，A7，A8)

图12～图15中“R”表示实际测量的真实值;“ID1”用条件数加权平均算法识别结果;“ID2”代表用常规的直接求逆法算出的结果。

图15 用响应点(A4，A7，A8)识别T2自谱Fig.15 Identification of T2 Auto-PSD at(A4，A7，A8)

总体上，条件加权算法较常规算法能有效提高识别精度。但由本组试验同样可看出，算法只能在一定程度上对误差进行改善，测点选择是载荷识别成败的关键。频响函数矩阵的条件数可以作为测点选择的依据，在实际反演之前，可将选定的测点组合的频响函数条件数曲线列出(如图11)，根据关心的载荷识别频段条件数较小原则挑选测点组合进行反演。如果希望整个频段平均误差最小，则求每组条件数各频段内平均值，取平均值最小的组合进行反演。另外根据笔者的经验，测点的选择还应当遵循如下一些原则:①响应测点应当避开模态振型节点处，应尽量分布在振型的峰谷处;②同方向测点不应当布置太近;③尽量布置在响应大的地方，提高信噪比;④如条件允许，增大系统阻尼能有效提高识别精度。

4 结论

针对随机载荷识别结果在固有频率附近出现误差较大的问题基于逆虚拟激励法提出了频响函数条件数的加权平均方法，它将频响函数与响应力进行重新组合，利用权值对条件数大的量少参与到虚拟激励力的平均计算中，能在一定程度上改善载荷识别精度。仿真和试验的误差比较验证了这一点。同时说明用不同响应组合频响函数条件数大小来选择参与计算的响应测点可大大提高识别精度和效率，两者结合起来将进一步减少误差。

方法由于涉及到多次求逆，如果测点数目很多势必增加一些计算的复杂度，因此，精度的获得是以牺牲计算时间为代价的，结合逆虚拟激励法的高效性，对于一般工程载荷识别问题，计算效率是可以接受的。

［1］任伟新.环境振动系统识别方法的比较分析［J］.福州大学学报 (自然科学版)，2001，29(6):80-86.

REN Wei-xin.Comparison of system identification methods using ambientvibration measurements［J］. JournalofFuzhou University(Natural Science Edition)，2001，29(6):80-86.

［2］ Barlett Jr F D，Flannelly W G.Model verification of force determination for measuring vibration loads［J］.Journal of the American Helicopter Society，1979，19(4):10-8.

［3］Giansante N，Jones R，Galapodas N J.Determination of inflight helicopterloads［J］. Journalofthe American Helicopter Society，1982，27(3):58-64.

［4］ Hillary B，Ewins D J.The use of strain gages in force determination and frequency response measurements［C］.Proceedings of 2th International Modal Analysis Conference 1984:627-634.

［5］孔 炜，冯顺山，朱春梅.载荷识别技术在火箭推力偏心测试中的应用［J］.北京理工大学学报，1999，19(5):68-75.

KONG Wei，FENG Shun-shan，ZHU Chun-mei.Measuring rocketthrustmisalignmentby using load identification technique［J］.Journal of Beijing Institute of Technology，1999，19(5):68-75.

［6］顾慧芝，聂君剑.载荷识别的等效点动标定法［J］.振动工程学报，1997，10(3):329-34.

GU Hui-zhi，NIE Jun-jian，DING Xi-hong.An equivalent point calibration method for dynamic load identifications［J］.Journal of Vibration Engineering，1997，10(3):329-334.

［7］吴大宏，赵人达.基于神经网络的混凝土桥梁荷载识别方法研究［J］.中国铁道科学，2002，23(1):25-38.

WU Da-hong，ZHAO Ren-da.Research on the method of load identification for concrete bridge based on neural network［J］.China Railway Science，2002，23(1):25-38.

［8］黄 林，袁向荣.小波分析在桥上移动荷载识别中的应用［J］.铁道学报，2003，25(4):97-101.

HUNG Lin，YUAN Xiang-rong.Application of wavelet analysis in identification of moving loads on a bridge［J］.Journal of The China Railway Society，2003，25(4):97-101.

［9］严 刚，周 丽.加筋复合材料结构的冲击载荷识别［J］.航空学报，2008，29(5):1150-1156.

YAN Gang，ZHOU Li.Impact load identification for stiffened composite structure［J］.Acta Aeronautica et Astronautica Sinica，2008，29(5):1150-1156.

［10］朱斯岩，朱礼文.运载火箭动态载荷识别研究［J］.振动工程学报，2008，21(2):135-149.

ZHU Si-yan，ZHU Li-wen.Dynamic load Identification on launch vehicle［J］.Journal of Vibration Engineering，2008，21(2):135-149.

［11］姜金辉，陈国平，张 方.多点平稳随机载荷识别方法研究［J］.振动工程学报，2009，22(2):162-167.

JIANG Jin-hui，CHEN Guo-ping，ZHANG Fang.Identification method of multi-point stationary random load［J］.Journal of Vibration Engineering，2009，22(2):162-167.

［12］林家浩，智 浩，郭杏林.平稳随机振动载荷识别逆虚拟激励法(一)［J］.计算力学学报，1998，15(2):127-36.

LIN Jia-hao， ZHI Hao， GUO Xin-lin. Inverse pseudo excitation method for loading identification ofstationary random vibration(1)［J］.Chinese Journal of Computational Mechanics，1998，15(2):127-36.

［13］Zhi H，Lin J H.Random loading identification of multi-Input-Multi-Output structure ［J］.Structural Engineering and Mechanics，2000，10(4):359-369.

［14］ Lin J H，Guo X L，Zhi H，et al.Computer simulation of structural random loading identification［J］.Computers and Structures，2001，79(4):375-387.

［15］Dongsheng L，Xinglin G，Shibin X.Loading identification of random excitations［C］.IMAC-XXI:A Conference ＆Exposition on Structural Dynamics，2003，

［16］ Guo X L，Li D S.Experiment study of structural random loading identification by the inverse pseudo excitation method［J］.Structural Engineering and Mechanics，2004，18(6):791-806.

［17］史荣昌.矩阵分析［M］.北京:北京理工大学出版社，1996.

［18］ Kong X，Liao J，Xu D.An improved method of structural random loading identification［C］.Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics(ISSCAA 2010)，Harbin，China，F 8-10 June］.IEEE.