基于多重多级动力子结构的Lanczos算法

张 盛，方 杰， 张洪武， 陈飙松

(1.大连理工大学 工业装备结构分析国家重点实验室，大连 116024;2.大连理工大学 运载工程与力学学部工程力学系，大连 116024)

随着工程技术的飞速发展，结构系统越来越庞大，越来越复杂，如飞机、大型轮船、高层建筑、大型机械和各种航天器。在分析计算大型复杂结构的动力特性和动力响应时，有限元离散化所得到的系统自由度是成千上万阶，有时甚至高达几十万阶、几百万阶。对于这种庞大的多自由度系统，用传统的求解特征值方法求解是十分困难的，甚至是不可能的。子结构方法是计算大型复杂结构动态特性十分有效的方法。

对于广义特征值问题［K］{φ}=λ［M］{φ}的求解，经典的子结构方法如模态综合法［1］，计算精度的好坏直接由选取的位移表达式即假设模态决定。界面位移凝聚法［2］是通过对子结构刚度阵和质量阵凝聚处理，达到降阶目的。胡海昌［3］利用解析的模态分析方法构造了约束界面模态综合法。邱吉宝等［4］采用半解析法提出了三类精确动态子结构方法。而对于一般广义特征值问题的求解，里兹向量法、子空间迭代法［5］、Lanczos算法［6］都是很实用的近似解法。喻永声等［7］提出利用动态子结构周游技术实现子空间迭代，求解大型结构的广义特征值方程，并取得较好的计算精度，但其需要迭代收敛判断;文献［8］提出利用子结构凝聚实现Lanczos算法的反迭代过程，实际上其求解仍然是在整体结构中进行。

Lanczos算法被认为是求解大型矩阵特征值问题的一种最有效的算法，由截断 Lanczos过程产生的Lanczos矢量空间能有效地逼近结构离散化模型的低维状态空间［9］，从而利用Lanczos矢量矩阵对数学模型进行降阶，求解结构低阶特征值。本文提出一种将多重多级子结构技术和Lanczos算法结合的方法。在子结构Lanczos迭代过程中，分别对每个子结构求解正交化系数和归一化系数，然后累加形成总体正交化系数和归一化系数，形成最终的三对角矩阵。数值算例结果表明该方法具有很高的计算效率和精度。

本文提出的基于多重多级子结构动力特征值分析的Lanczos算法已在具有自主版权的CAE软件JIGFEX中实现。

1 多重多级子结构的Lanczos方法

对于广义特征值方程:

其中［K］和［M］分别为结构的刚度矩阵和质量矩阵。文献［7］提出了一种基于多重子结构的子空间迭代法，利用子结构周游树技术实现子空间迭代。本文利用文献中提到的子结构方法，实现基于多重子结构的Lanczos方法，计算效率较之于前者取得很大的进步。

Lanczos算法本质与子空间迭代法类似，都属于向量反迭代法和Rayleigh-Ritz法相结合的一种方法，但它结合得巧妙，使计算过程大大简化。其基本思想主要包括三步:反迭代、正交化和模归一化处理。本文主要是利用多重多级子结构周游树技术实现这三部分，并求解方程(1)。

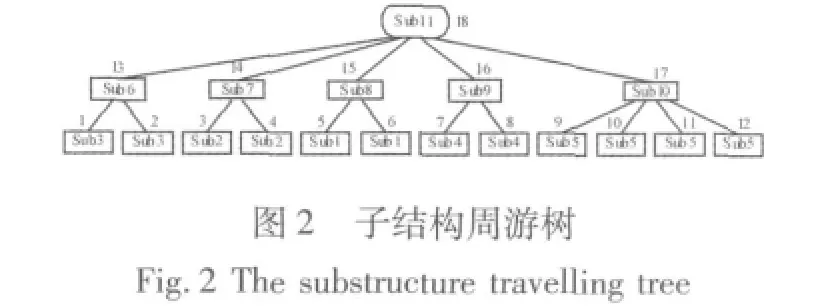
考虑图1所示的子结构模式划分，整体结构为一平板，被离散成为一系列子结构模式，其中1、2、3、4、5为基本子结构模式，通过组装调用形成6、7、8、9、10及11子结构模式，其中Sub11为顶层子结构模式。子结构周游树总节点数为18，子结构周游树中子结构调用关系见图2所示。

方程(1)右端可看成广义外力向量{F}，对于k≥1，Lanczos反迭代可依下式进行:

其中，

利用多重子结构静力分析方法可以很方便求解式(2)中的位移向量}k+1。设子结构成员数为comp，s为子结构成员号。首先对子结构成员序列中的每一个子结构成员，利用式(3)形成广义外力向量{F}k+1，并将方程(2)写成如下形式:

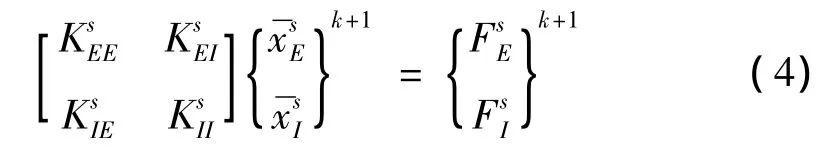
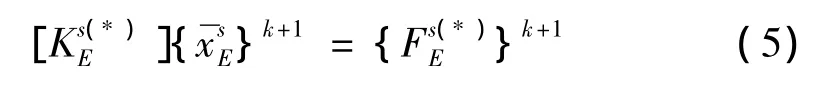
其中，

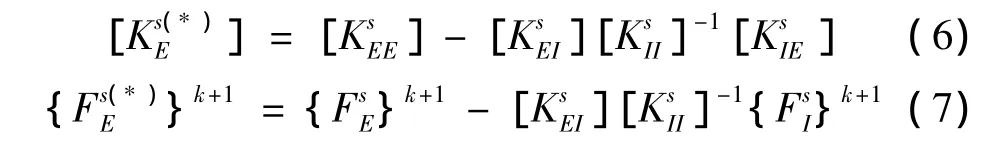
求解顶层子结构静力方程:

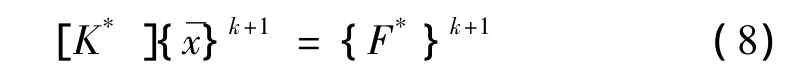
通过子结构前序周游回代求解下层每个子结构的内部位移向量:

图2 中的子结构前序周游顺序是 18，13，1，2，14，3，4，15，5，6，16，7，8，17，9，10，11，12。于是所有子结构位移自由度即可求出，完成式(2)中的反迭代。

Lancozs算法正交化由下式进行:

其中αk、βk是正交化系数，由下式确定:

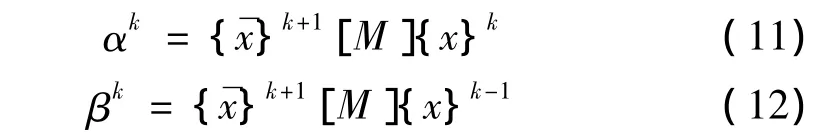
式(10)中的位移向量都为整体结构下的位移向量，也是全体子结构位移向量的组合，显然式(10)可以转化为对每个子结构的正交化:

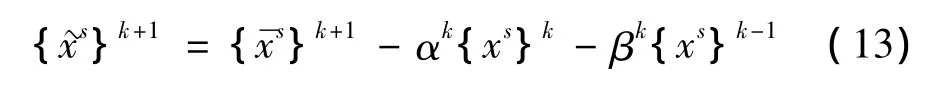
［Ms］为质量阵，且对于集中和协调质量阵同样有效，于是可以得到:

计算中，为避免式(10)中的正交化不彻底，往往需要加入重正交化步骤，用上述的步骤同样可以完成重正交化:

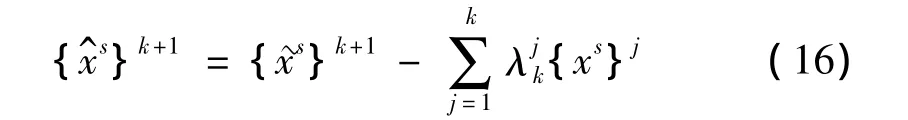
Lanczos向量的归一化系数也可以利用类似的步骤完成。先考虑下式:

其中:

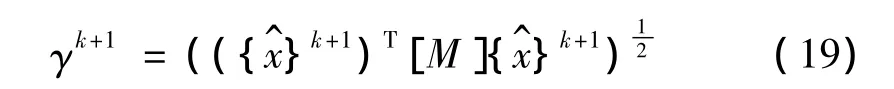
类似于式(14)、(15)，分别计算每个子结构位移向量的归一化系数，并累加得:

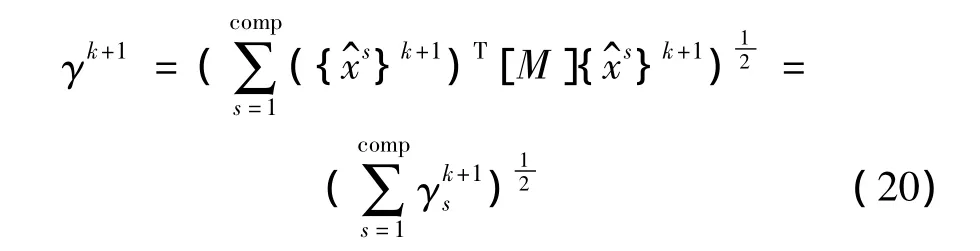
分别对每个子结构归一化:

对每个子结构进行模归一化即可完成对整体结构的归一化处理。事实上，上述的正交化和归一化中，所有子结构位移自由度都参与了计算，这与整体结构参加计算完全相同，计算精度并不受子结构划分的影响，计算量却大大降低。

设求解特征值个数为n，特征子空间阶数为m(一般取m=n×2)，k是迭代次数。程序流程如图3所示，多重子结构Lanczos方法计算可按如下步骤进行:

(1)迭代次数k取0，对每个子结构s，随机选取初始矢量{xs}0。

(2)迭代次数k进1。

(3)对每个子结构形成式(3)中的广义外力向量{Fs}k。

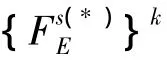
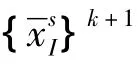
(6)利用式(14)、(15)求解每个子结构的正交化系数并累加得到全局正交化系数。

(7)利用式(13)对每个子结构进行正交化。

(8)利用式(16)、(17)对每个子结构进行重正交化。

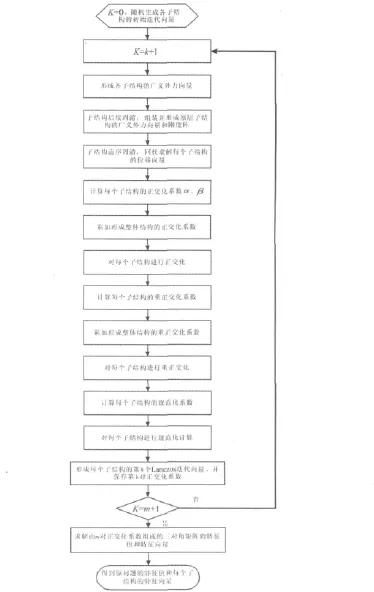
图3 本文方法主要程序流程Fig.3 The main program flowchart of the proposed method

(9)利用式(20)求得每个子结构成员的归一化系数，并累加得到全局归一化系数。

(10)利用式(21)对每个子结构成员进行归一化计算，并得到第k个Lanczos向量。

(11)返回步骤(2)，进行下一步迭代，直至k=m+1。

(12)形成由正交化系数组成的三对角阵。

对m×m阶三对角阵的特征值方程:

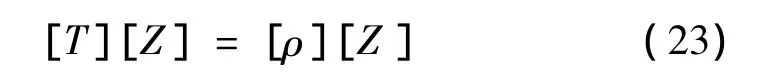
求解得:

则方程(1)的解为:

选择将随机向量{xs}0进行一次反迭代和模归一化后作为第一个Lanczos向量{xs}1。

本文算法与全结构算法计算效率的对比与静力分析情况类似。算法的关键公式为平衡方程式(2)求解、式(10)正交化及式(18)归一化，因此处未引入近似，故算法迭代次数以及式(10)、式(18)的计算复杂度与全结构Lanczos算法一致。在计算效率方面，主要考察式(2)，设全结构共有n个自由度，则全结构模型求解式(2)的计算复杂约为O(n3);若利用本文算法将结构等分为两个子结构，子结构自由度为n/2，子结构的出口节点自由度为w，则按多重多级子结构求解式(2)的计算复杂度约为O((n/2)3+(n/2)3+w3)=O(n3/4+w3);一般w远小于n，因此采用本文算法计算效率有优势。对于复杂结构若子结构划分得当，优势将更显著。

本文工作是在基于我国自主开发的CAE软件系统JIGFEX 中实现的［10-11］。

2 计算实例

算例一 考虑图1所示的矩形板，几何尺寸10 m×20 m×0.05 m，边界条件为:平面内位移固定，即dx=dy=θz=0;沿x=0 和x=10，dz=θy=0;沿x=0 和x=10，dz=θx=0;弹性模量 200 GPa，泊松比 0.3，密度8.0 ×103kg/m3。

采用图1中的子结构模式划分，利用本文方法求解前10阶模态，同时对整体结构用MSC.Nastran求解，两者都采用大小相同的三角形壳单元，总单元个数相等，前十阶自振频率计算结果如表1所示。计算结果表明本文子结构求解的计算精度与整体结构求解相当，显示了本文方法具有很好的计算精度。图4为平板结构的前4阶振型。

表1 平板前10阶频率Tab.1 The free vibration frequencies of the flat

图4 平板前四阶振型Fig.4 The first four vibration model of plate

算例二 图5所示为某型号运载火箭整体结构。箭体主体为圆筒加锥段组成，并附有夹筋梁，分为一子级、二子级、整流罩等几个部分。模型的几何尺寸为:一子级直径为3.2 m，长度为16 m;二子级直径3.2 m，长度8 m;三子级直径为2.8 m，长度为6 m;整流罩直径为4 m，长度为4 m。选用的材料为铝合金:弹性模量 69 GPa，泊松比 0.3，密度 2.7 ×103kg/m3，梁截面尺寸为0.02 m×0.02 m。图5(a)中整体结构有限元网格划分共有节点7 037个，梁单元4 184个，三角形板单元13 840个。

图5 三级火箭体子结构模式Fig.5 The substructure models of the three-leval rocket

按子结构方式划分火箭，将整体火箭分为一子级、二子级、三子级、前锥段、后椎段，整流罩筒体段和整流罩锥段7段，根据结构圆周对称的特点再将这7段沿圆周分为4部分，对这7个1/4火箭段进行建模，利用子结构的组装调用最后形成图5(b)中的整体结构。整个结构分为15个子结构模式，其中7个基本子结构模式，共有36个超级单元。图5(b)中为火箭体的子结构模式序列。利用多重多级子结构Lanczos方法求解子结构模型前10阶模态，并在MSC.Nastran中计算整体结构前10阶自振频率。

表2 火箭前10阶自振频率Tab.2 The free vibration frequencies of the rocket

表2为分别利用子结构模型与整体结构模型计算的前10阶自振频率，二者相对差值均不到0.5%，表现了多重多级子结构Lanczos方法良好的计算精度。

3 结论

本文方法在求解大型结构动力特性时具有较高的计算精度和效率。数值算例表明利用本文方法求解与整体结构计算结果相对差值皆在1%以下;较之多重子结构子空间迭代［7］，本文方法不需要迭代收敛判断，每次迭代仅一个向量参与计算，效率更高。

［1］Hurty W C.Dynamic analysis of structural systems using component modes［J］.AIAA Journal，1965，3(4):678-685.

［2］ Guyen R J.Reduction of stiffness and mass matrice［J］.AIAA Journal，1965，3(2):380-380.

［3］胡海昌.多自由度结构固有振动理论［M］.北京:科学出版社，1987.

［4］邱吉宝，向树红，张正平.计算结构动力学［M］.合肥:中国科学技术大学出版社，2009.

［5］Bathe K J，Wilson E L.Solution methods for eigenva lue problems in structural mechanics［J］.International Journal for Numerical Methods in Engineering， 1973， 6(2):213-226.

［6］徐稼轩，郑铁生.结构动力分析的数值方法［M］.西安:西安交通大学出版社，1993.

［7］喻永声，林家浩.超大型结构特征值问题求解的多重子结构子空间迭代［J］.工程力学，2003，20(6):149-156.

［8］张汝清，胡 宁.大型结构特征值问题的Lanczos子结构并行算法［J］.计算结构力学及其应用，1991，8(4):359-364.

［9］刘 豫，孙 秦.大型结构动力特性的Lanczos数值计算方法及程序设计［J］.科学技术与工程，2008，8(4):2010-1015.

［10］钟万勰，李锡夔.JIGFEX系统及其在大型结构分析中的应用［J］.土木工程学报.1982，15(3):20-28.

［11］ 张洪武，喻永声，纪 峥，等.结构分析有限元程序JIGFEX和它的新发展［J］.计算结构力学及其应用，1995，12(3):292-297.