重载列车过桥时桥梁的垂向动力分析

龙卫国，蒋丽忠，陈令坤

(1.中南大学土木建筑学院，湖南长沙，410075;2.南华大学数理学院，湖南衡阳，421001)

列车通过桥梁时将引起桥梁结构的振动，而桥梁的振动又反过来影响车辆的振动，这种复杂的相互作用就是车辆与桥梁之间耦合振动，车桥系统是一个复杂的时变系统。吴定俊等［1］研究了高速铁路桥梁梁墩基础体系列车过桥动力分析;王少钦，苏木标，王解军等［2-4］研究了变速移动荷载作用下简支梁桥的动力响应及共振分析;彭献等［5］研究了车-桥系统的振动分析及控制;还有许多学者研究了轨道不平顺［6-9］等等。总体看来建立车桥系统运动方程常用以下两种方法:①将车辆与桥梁的所有自由度耦联在一起，建立统一的方程组，进行同步求解;②将车桥系统以轮轨接触处为界，分为车辆与桥梁两个子系统，分别建立车辆与桥梁的运动方程，两者之间通过轮轨接触处的位移协调条件与轮轨相互作用力的平衡关系相联系，采用迭代法求解系统响应。目前对重载列车过桥时的车-桥系统的动力分析很少见文献报道，且车辆计算模型的自由度也过于简单(二个自由度:沉浮和点头)。

本文将提出6个自由度的车辆振动分析模型和空间梁段单元动力分析模型，采用第二种方法来建立车桥系统耦合振动方程，对重载列车作用下的简支梁桥的竖向动力响应进行分析。

1 车－桥系统动力计算模型

列车过桥时，列车对桥梁的相互作用包括机车和车辆对桥梁的相互作用，然而机车(指内燃机车或电力机车)对桥梁的作用，主要包括:机车的静轴重移动荷载及其簧承部分的振动和簧下质量及悬挂弹簧刚度、阻尼等。虽然这些因素对桥梁的竖向振动都有一定的影响。在较高速度情况下，因为机车在桥上作用的时间非常短暂，不会激起桥梁较大的振动，因此在以下的计算中不考虑机车的作用。车辆的计算模型如图1所示。

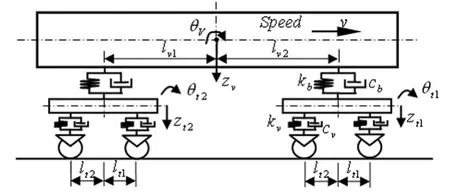
图1 车辆模型Fig.1 A vehicle model

设列车过桥时(在t时刻)桥上有第K到第M个轮对，车辆与桥梁在同一竖直平面内相互作用(如图2所示)。列车的每一辆车的车体和转向架均理想化为具有二个自由度(沉浮和点头)的刚体;车辆的竖向两系悬挂弹簧被认为是串联线性弹簧，其刚度用等效弹簧刚度代替;相邻车辆之间的联接器假定为铰接，各轮对与轨道之间始终保持接触。

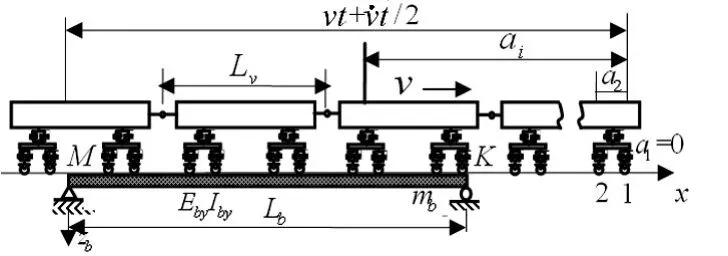
图2 车-桥系统模型Fig.2 Vehicle-bridge system model

2 车－桥系统运动方程

2.1 车辆运动方程

根据车辆的计算模型，由达朗伯原理可推导出每一辆车的运动方程，

车体:

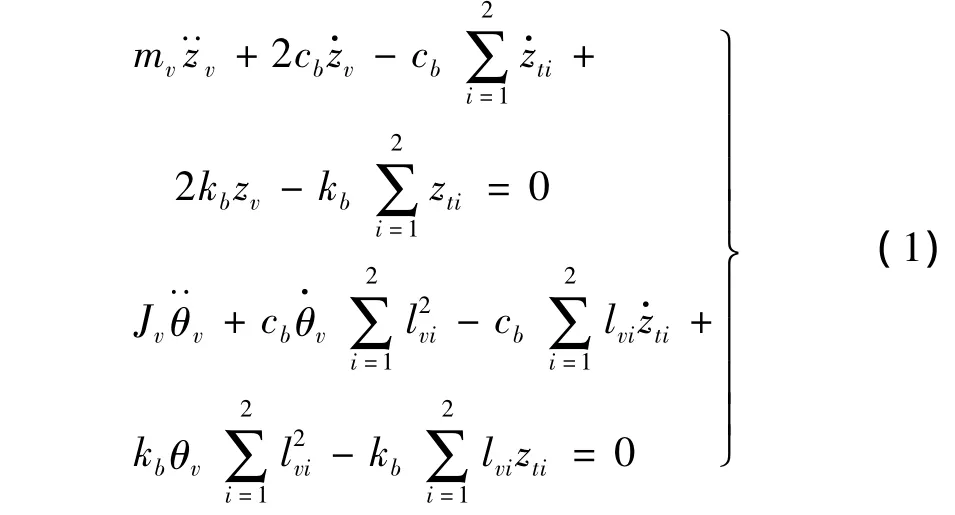
转向架:(i=1，2)

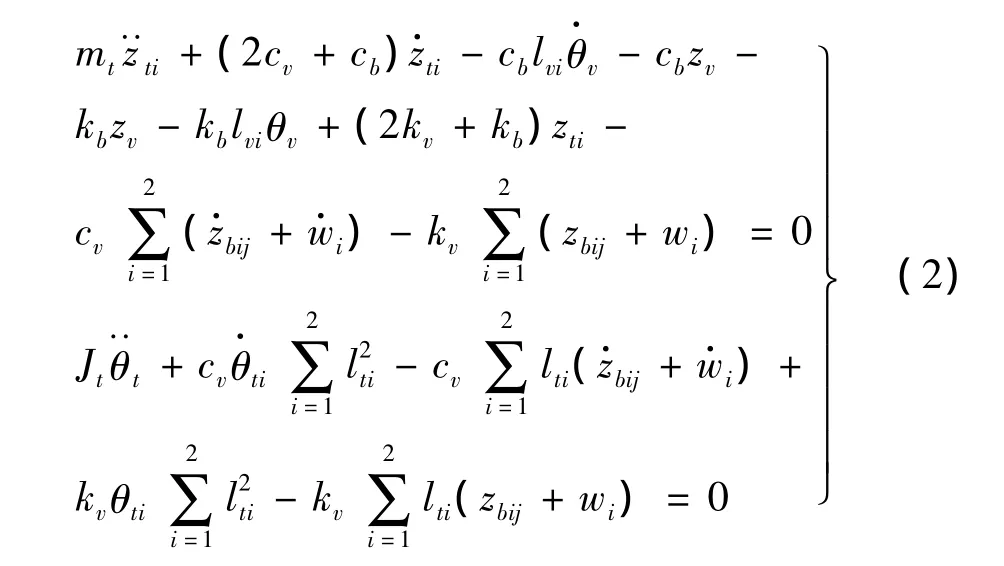
其中:zv和θv分别为车体的竖向和点头位移;zti和θti分别为第i个转向架的竖向和点头位移;zb(x，t)为桥梁的竖向位移;w为竖向轨道不平顺;kv、kt和cv、ct分别为车辆一、二系悬挂弹簧的阻尼系数和刚度系数;mv和Jv分别为车体的质量和点头惯性矩;mt和Jt分别为转向架的质量和点头惯性矩;l、lvi、lti的意义见图1。

2.2 桥梁运动方程

考虑轨道不平顺，则桥梁的运动方程为:

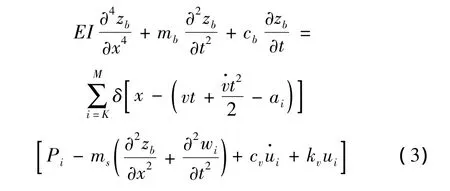
式中:EI、mb和cb分别为桥梁的竖向抗弯刚度、单位长度质量和阻尼系数;ms为列车第i轮对的簧下质量;Pi为列车第i轮对的静轴重;ai为列车第i轮对距第1轮对的水平距离(列车最前端的轮对为第1轮对，依没向后分别为第2，3，…，N轮对);ui为列车第i轮对悬挂弹簧的变形(见式(6));v为列车运行速度;δ(ξ)为Dirac函数。

对于式(3)，考虑前L阶振型，用振型分解方法可得桥梁竖向振动位移:

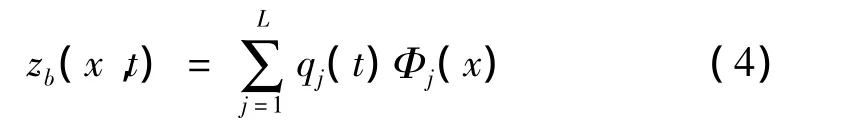
其中:Φj(x)=sin(jπx/Lb)为桥梁的第j阶振型;Lb为桥梁的跨度。将式(4)代入式(3)并利用振型的正交性，整理后可得桥梁第j阶振型的运动方程:

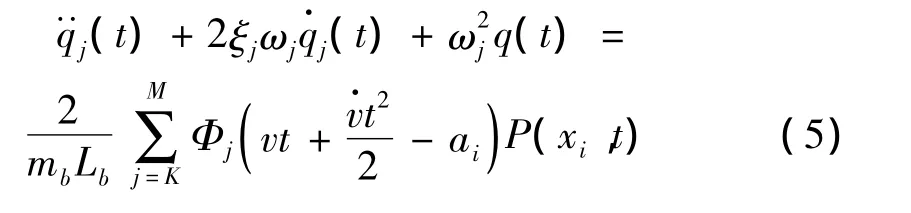
其中，

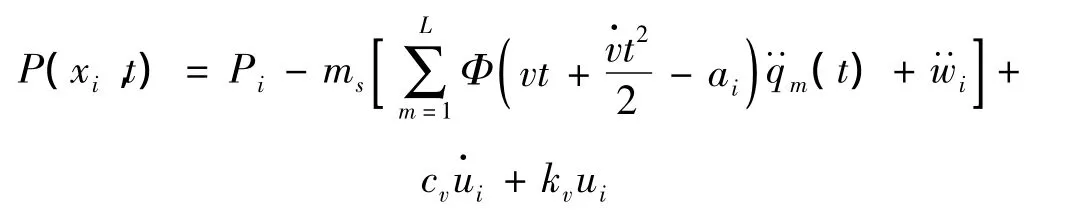
式中的ui和的计算式可表示为:

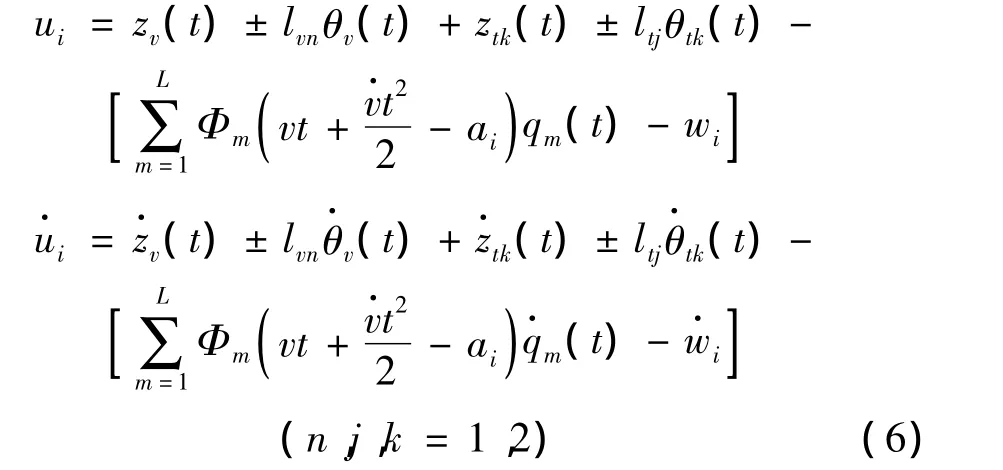
其中:wi为列车第i轮对下轨道不平顺;zv和θv分别为第i轮对所对应的车体(车辆)的竖向位移和点头位移;zik和θik分别为第i轮对所对应的车体的第k个转向架的竖向位移和点头位移。

联立式(1)、(2)和(5)可得车-桥系统运动方程。

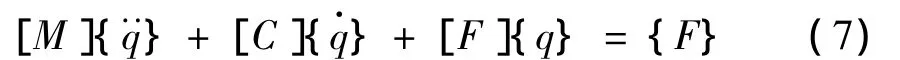
3 车－桥系统的动力分析

本文采用跨度为Lb=32 m的某重载铁路桥梁，其截面由4个T字型截面构成，其弹性模量E=35.5 GPa，惯性矩Iz=5.38 m4，单位长度的质量mb=93 000 kg/m。重载列车采用轴重增大轴距不变的计算荷载图式，车辆长度均为lv=12 m，lv1=lv2=4.1 m，lt1=lt2=1.25 m，轮对的质量mw=250 kg，转动惯量Jw=5 400 kg·m2。kv=kb=300 kN/m，cv=cb=60 kN·s/m。

考察变速车辆与轨道不平顺桥梁系统，根据德国高干扰线路(普通铁路)轨道不平顺时域样本，如图3所示，其幅值为A。

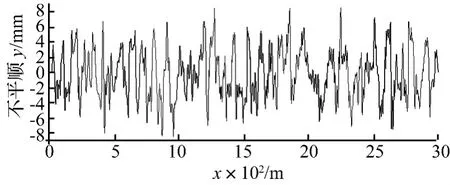
图3 德国普通铁路轨道不平顺时域样本Fig.3 Time domain samples of track irregularity of German general railway

3.1 列车速度对车－桥系统的影响

列车以初速度v=25、50、75、100 km/h的速度运行，A=2 mm，列车的静轴重均为Pt=250 kN，转动惯量Jv=27×105kg·m2，计算结果如图4、5所示。

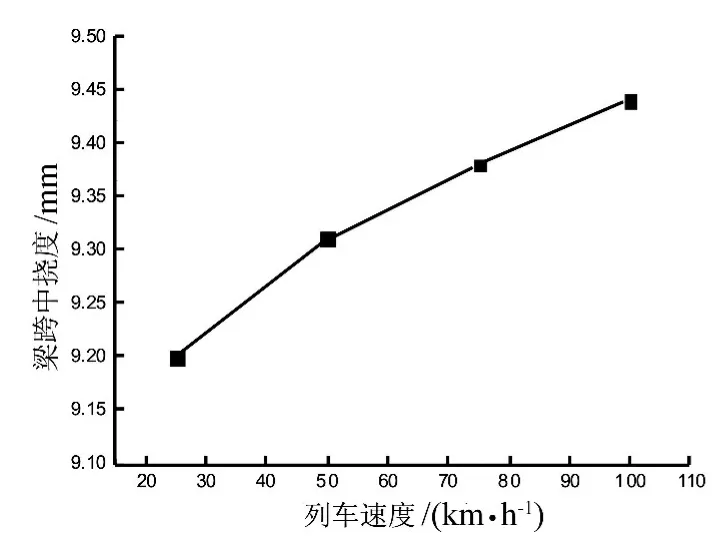
图4 列车速度与挠度的关系曲线Fig.4 Curve of deflection and train speed

图5 列车速度与竖向加速度的关系曲线Fig.5 Curve of vertical acceleration and train speed

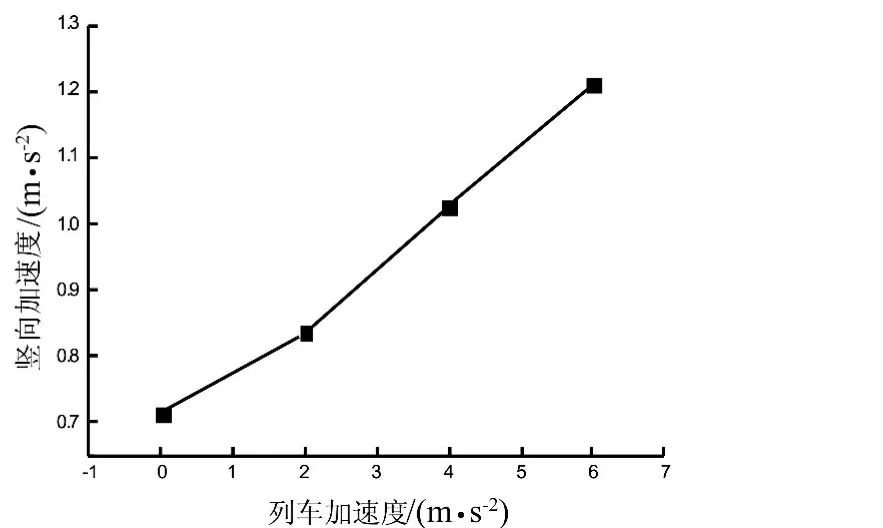
图6 列车加速度与挠度的关系曲线Fig.6 Curve of deflection and train acceleration

图7 列车加速度与竖向加速度的关系曲线Fig.7 Curve of vertical acceleration and train acceleration

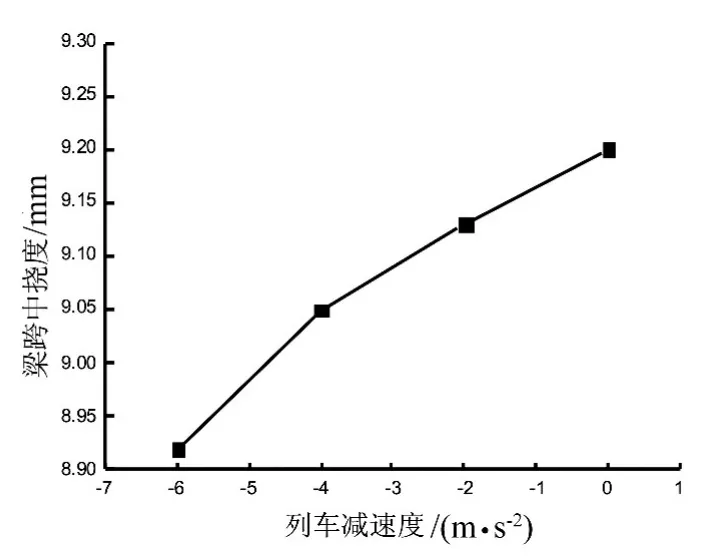
图8 列车减速度与挠度的关系曲线Fig.8 Curve of deflection and train deceleration

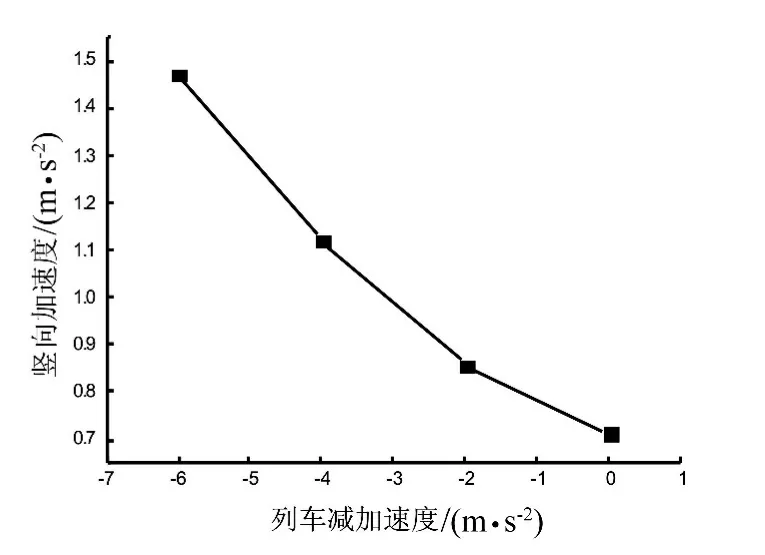
图9 列车减速度与竖向加速度的关系曲线Fig.9 Curve of vertical acceleration and train deceleration

从图4、5可知，随列车速度的增加桥梁的跨中挠度和竖向加速度都有增加，但竖向加速度增幅更大。

3.2 列车加速运动对车－桥系统的影响

列车的初速度v=70 km/h，加速度=0、2、4、6 m/s2，A=2 mm。列车的静轴重为Pt=250 kN，转动惯量Jv=27×105kg·m2，计算结果如图6、7所示。

从图6、7可知，随列车的加速度的增加桥梁跨中的挠度和竖向加速度都有增加，但挠度增加幅度较小，但竖向加速度增幅较大。

3.3 列车减速运动对车－桥系统的影响

列车的初速度v=70 km/h，加速度=0、-2、-4、-6 m/s2，A=2 mm。列车的静轴重为Pt=250 kN，转动惯量Jv=27×105kg·m2，计算结果如图8、9所示。

从图8、9可知，桥梁跨中的挠度随减速度的绝对值增大而减小，但桥梁跨中的竖向加速度随列车的减速度的绝对值增加而增加，且增加幅度越来越大。

3.4 列车轴重对车－桥系统的影响

列车的初速度v=70 km/h，加速度=0，A=2 mm。列车的静轴重分别为Pt=250、280、300、330 kN，转动惯量分别为Jv=27 ×105、30.24×105、32.4 ×105、35.64 ×105kg·m2，计算结果如图 10、11 所示。

从图10、11可知，随列车轴重的增加桥梁跨中的挠度和竖向加速度都有增加，且挠度和竖向加速度的增幅均较大，且竖向加速度的增幅不是一般线性增加。

3.5 轨道不平顺幅值对车－桥系统的影响

列车的初速度v=70 km/h，加速度=0，A=2、4、6、8 mm。列车的静轴重均为Pt=250 kN，转动惯量Jv=27 ×105kg·m2，计算结果如图12、13 所示。

从图12、13可知，随轨道不平顺的幅值增加桥梁跨中的挠度和竖向加速度都有增加，但桥梁挠度增加幅度不大，但竖向加速度增幅较大。

图10 列车轴重与挠度的关系曲线Fig.10 Curve of deflection and axle weight of train

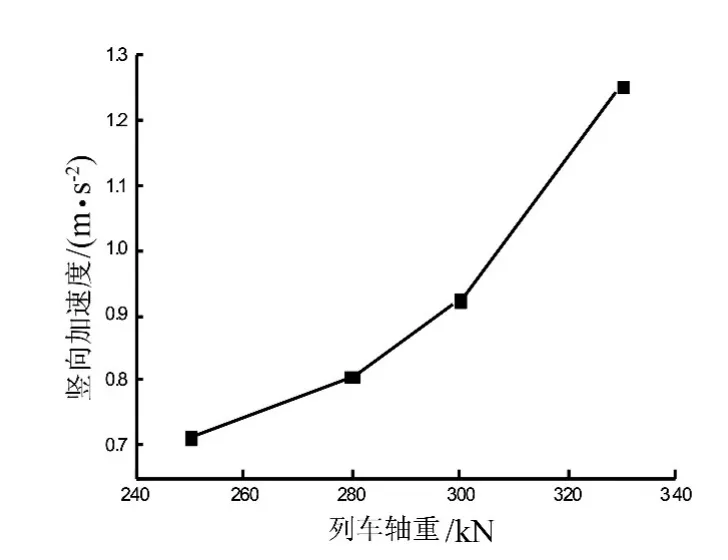
图11 列车轴重与竖向加速度的关系曲线Fig.11 Curve between vertical acceleration and axle weight of train

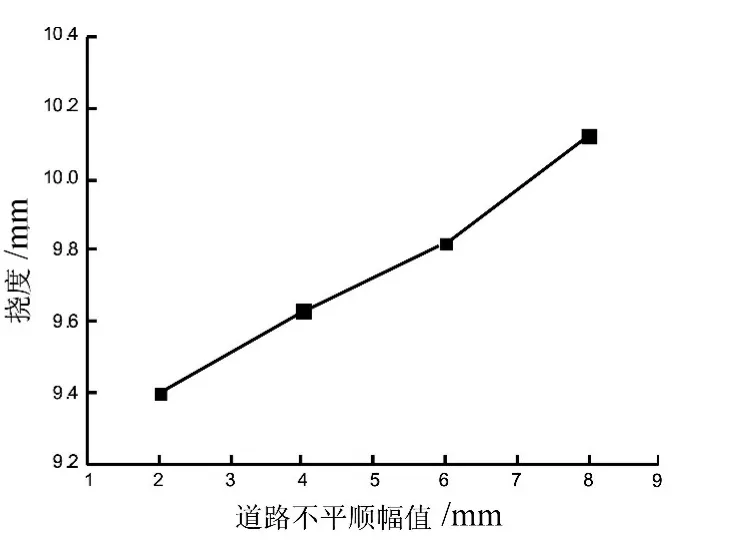
图12 轨道不平顺幅值与挠度的关系曲线Fig.12 Curve of deflection and amplitude of rail irregularity

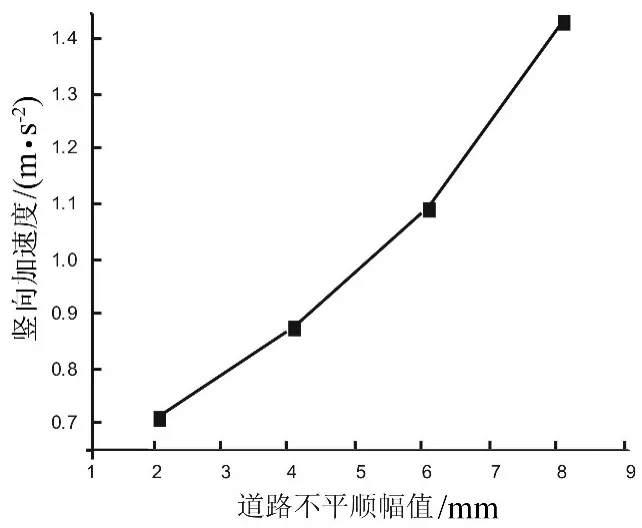
图13 轨道不平顺幅值与竖向加速度的关系曲线Fig.13 Curve of vertical acceleration and amplitude of rail irregularity

4 结论

建立了重载铁路车-桥系统的动力相互作用模型，推导出其动力学方程，编制程序求解了列车过桥时桥梁的动力响应。通过数值计算及分析，可以得到如下结论:

(1)重载铁路桥梁的跨中挠度和竖向加速度随列车的轴重增大而增大，且增幅较大，因此，在既有铁路线上增大营运列车的轴重时，必须要对桥梁重新进行检定;

(2)重载铁路桥梁的跨中挠度和竖向加速度随列车的速度、加速度及轨道不平顺幅值的增大而增大，它们引起挠度的增幅较小，但加速度增幅均较大，直接影响列车过桥时的平稳性;

(3)重载铁路桥梁的跨中挠度随列车的减速度的绝对值增大而减小。说明列车在桥梁上减速运行，一般不影响桥梁的挠度指标但同样会影响列车过桥时的平稳性。

［1］吴定俊，周建民，余 华.高速铁路桥梁梁墩基础体系列车过桥动力分析［J］.上海铁道大学学报，2000，21(10):44-49.

WU Ding-jun，ZHOU Jian-min，YU Hua.Dynamic analysis of vehicle-bridge system including pier and foundation［J］.Journal of Shanghai Tiedao University，2000，21(10):44-49.

［2］王少钦，夏 禾，郭薇薇，等.变速移动荷载作用下简支梁桥的动力响应及共振分析［J］.振动与冲击，2010，29(2):26-30.

WANG Shao-qin，XIA He，GUO Wei-wei.et al.Dynamic response and resonance analyses for a simply-supported bridge under speed-varying loads［J］.Journal of Shanghai Tiedao University，2010 ，29(2):26-30.

［3］苏木标，李建中，邹振祝，等.高速铁路简支梁桥有载动力特性分析［J］.工程力学，2002，19(3):137-142.

SU Mu-biao，LI Jian-zhong，ZOU Zhen-zhu，et al.Analysis of loaded dynamic characteristics of simply supported beam bridges on high speed railway［J］.Engineering Mechanics，2002，19(3):137-142.

［4］王解军，张 伟，吴卫祥.重载汽车荷载作用下简支梁桥的动力反应分析［J］.中南公路工程，2005，30(2):55-67.

WANG Jie-jun，ZHANG Wei，WU Wei-xiang.Analysis of dynamics responses of simply supported girder bridge under heavy moving vehicles［J］. Central South Highway Engineering，2005，30(2):55-67.

［5］彭 献，殷新锋，茆秋华.车-桥系统的振动分析及控制［J］.动力学与控制学报，2006，4(3):253-258.

PENG Xian，YIN Xin-feng，MAO Qiu-hua.Vibration analysis and control on vehicle-bridge system［J］.Journal of Dynamics and Control，2006，4(3):253-258.

［6］陈宪麦，王 澜，陶夏新，等.基于小波分析理论的轨道不平顺分析［J］.铁道工程学报，2008，112(1):57-61.

CHEN Xian-mai，WANG Lan，TAO Xia-xin，et al.Analysis of track irregularity with wavelets analysis theory［J］.Journal of Railway Engineering Society，2008，112(1):57-61.

［7］黄俊飞，练松良，宗德明，等.轨道随机不平顺与车辆动力响应的相干分析［J］.同济大学学报(自然科学版)，2003，31(1):16-20.

HUANG Jun-fei，LIAN Song-liang ZONG De-ming，et al.Analysis of coherence between track random irregularity and vehicle dynamic response［J］.Journal of Tongji University(Natural Science)，2003，31(1):16-20.

［8］张 昕，蒋 通.考虑轨道不平顺的车-桥动力分析［J］.力学季刊，2003，24(1):15-22.

ZHANG Xin，JIANG Tong.Dynamic analysis of train-bridge system considering rail irregularity［J］.Chinese Quarterly of Mechanics，2003，24(1):15-22.

［9］曲 名，许玉德.基于小波的列车加速度和轨道不平顺分析［J］.华东交通大学学报，2008，25(5):36-41.

QU Ming， XU Yude.An analysis of the relationship of acceleration and track irregularity based on wavelet［J］.Journal of East China Jiaotong University，2008，25(5):36-41.