天线转台倾斜状态下雷达测高精度优化方法*

徐绵起，王斌，徐瀚智

(中国人民解放军94981部队，江西南昌 330200)

0 引言

实际工作中，三坐标相控阵雷达提供的高度数据往往存在较大偏差，这一状况普遍存在，影响了预警探测雷达情报质量，是困扰预警探测雷达情报工作的一大难题。本文分析了天线转台倾斜对三坐标雷达测高精度的影响，通过对测高误差进行量化分析，研究提出了针对天线转台倾斜引起的三坐标雷达测高误差的修正方案。

1 三坐标雷达测高误差的数学表征［1－3］

三坐标相控阵地面情报雷达，水平方向采用机械扫描，垂直方向采用波束电扫描，目标的高度信息是由目标测距和波束仰角计算出来的。根据物理意义，利用几何方法，可以推导出目标高度的计算公式为

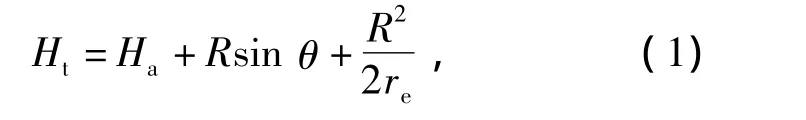
式中:Ht为目标高度;Ha为雷达天线中心的高度;R为目标至雷达天线中心的距离;θ为波束指向目标的仰角;re为考虑大气折射效应后的等效地球半径，

式中:r0为地球真实半径，r0=6 370 km;k为一个系数，在标准大气折射状况下，

于是，re=kr0=8 490 km。

这里要顺便提醒的是，R为目标斜距，它通过雷达波在空中的来去传播时间便可计算得知。而目标的雷达情报距离为

由式(1)可知，测高误差是由天线高度标定误差、测距误差和仰角误差共同决定的。由于引起测距误差和仰角误差的因素很多，而且有些因素具有随机性，从而使得测高误差具有随机性。根据误差理论，测量误差常用误差的均方根值来表征。

设测距误差的均方根值为σR，测仰角误差的均方根值为σθ，测高误差的均方根值为σH，天线高度标定误差后面再讨论。根据误差理论，由式(1)可推导出［4］:

对于对空情报雷达，式(5)等式右边的第2项常常被省略掉，理由是测距误差很小，第2项相对第1项可省略不计。于是，便有以下表征测高误差的简化公式［5］:

需要注意的是，式(6)中，σθ的单位是 rad，σH和R取同一量纲。

从式(6)可以看出，三坐标雷达的测高误差主要由波束仰角误差引起。

2 天线转台倾斜引起的波束仰角指向误差量化分析［6－8］

天线转台倾斜，或称天线转台水平误差，会引起天线波束仰角误差。

天线转台水平误差是由于天线转台水平度发生偏差，使得天线波束仰角发生偏移，而根据这个仰角来计算高度，肯定会产生高度误差。

天线转台的水平调整，受到水平传感器精度、调平控制软件设置的精度门限和调平机构执行能力的制约。针对2种型号的三坐标雷达，通过计算发现，水平调整结束后，天线转台的水平精度难以满足高精度测高的要求。

当天线水平旋转时，天线转台水平误差所引起的波束仰角偏移是大小和方向都在变化的，也就是说测高误差是随天线水平旋转而变化的。考虑到天线遭遇过大风、调平机构失修、阵地下沉、雷达机动等因素，天线转台的水平度是很容易发生变化的，它的微小变化，引来的是大的测高误差。

现以某高机动三坐标雷达为例。调平精度σ主要由主水平传感器的测量精度σ1和调平软件设定的门限σ2决定。在其技术说明书中介绍，水平传感器精度 σ1≤1'，调平软件设定的门限 σ2≤2'，所以调平精度σSB=σ1+σ2≤3'。先不论这个值是否合理，就以这个理想的值来分析调平精度σSB引起的测高误差。以观测300 km处、10 km高的目标为例，此时波束仰角在2°附近，天线转台水平误差所引起测高误差为260 m，如图1所示。

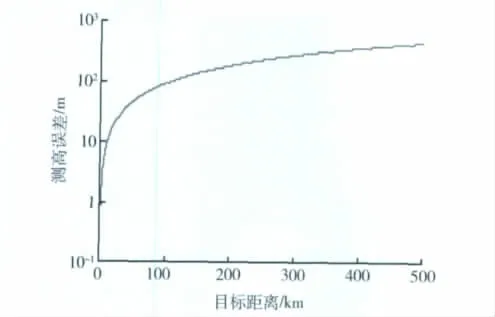
图1 波束偏差3'所引起的测高误差Fig.1 Altimetry definition error for 3'beam elevation angle

仍以某高机动三坐标雷达为例。天线阵面平坦度误差理论值为σXM=0.02°。综合考虑天线阵面平坦度误差和天线转台水平误差，则天线波束最大偏差可达4.2'。仍以观测300 km处、10 km高的目标为例，此时天线波束偏差所引起测高误差为366 m，如图2所示。

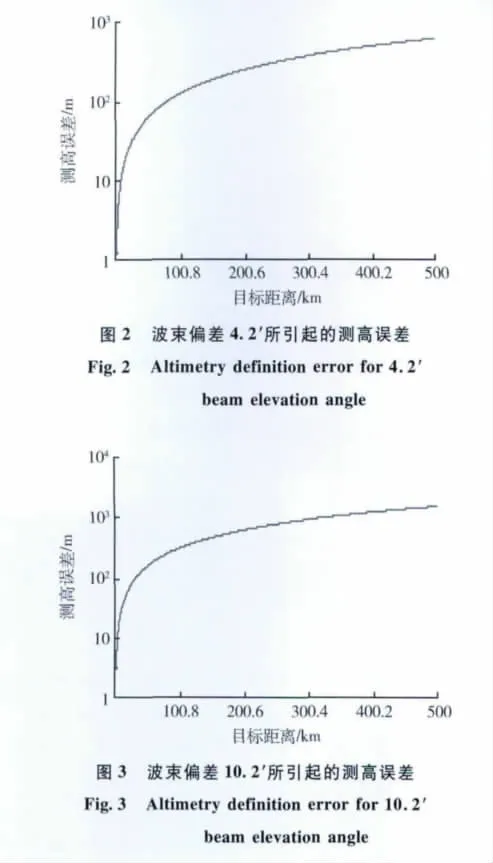
再考虑天线阵面升降定位容差，理论值为σSJ=0.1°。综合以上3项，则天线波束仰角最大偏差可达10.2'。仍以观测300 km处、10 km高的目标为例，此时天线波束偏差所引起测高误差为890 m，如图3所示。

查阅了国内外水平传感器产品相关资料，最好的测量精度性能是3＇，没查到精度1＇的水平传感器，但若以弧度表示则为0.01 rad。还有一种表示方法为1 mm/m，即1 m之内偏差1 mm，这与0.01 rad，0.05°或3＇是同一个精度、不同的表示方法。所以，本文作者认为，水平传感器测量精度为1＇的表述是值得商榷的。现以水平传感器测量精度为3＇进行分析，则此雷达的调平精度为5＇。以上讨论中，天线阵面平坦度误差是以0.02°即1.2＇计算的。事实上，本文作者查阅了国内外水平检测仪产品相关资料，最好的测量精度性能是3＇。这种情况下，综合以上3项，则天线波束仰角最大偏差可达14＇。

仍以观测300 km处、10 km高的目标为例，此时天线波束偏差所引起测高误差为1 222 m，如图4所示。

若天线遭遇大风、调平机构失修、阵地下沉、雷达机动到低标准阵地等因素，天线转台水平误差有可能超过20＇。仍以观测300 km处、10 km高的目标为例，此时天线标定误差所引起测高误差为1 841 m，如图5所示。

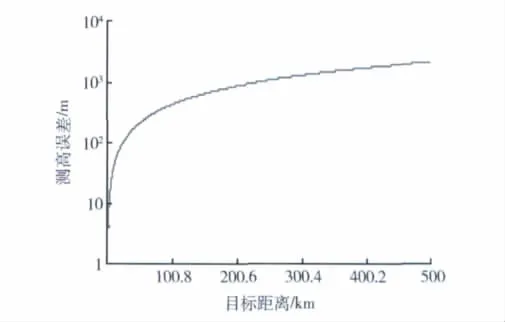
图4 波束偏差14'所引起的测高误差Fig.4 Altimetry definition error for 14'beam elevation angle

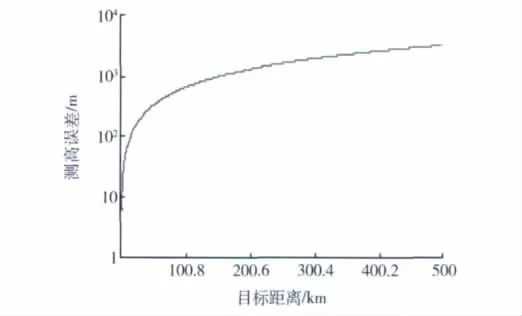
图5 天线转台水平误差20'所引起的测高误差Fig.5 Altimetry definition error for 20'beam elevation angle

由以上分析可以看出，天线存在的水平误差足以引起很大的测高误差。然而，天线的水平误差，修正起来有一定的难度，必须设计一种技术方案，对天线转台的水平度进行实时跟踪检测，以此为依据，通过对数据终端的高度数据进行实时修正，或通过改变波束仰角指向的方法，达到对测高误差实时修正的目的。

3 天线转台水平误差大小的判定［9－10］

天线转台水平误差所引起的波束仰角偏差是随着天线水平旋转而动态变化的。阵地条件下，实时发现测高误差的简单易行的办法是将一次雷达的测定高度值与二次雷达的高度数据进行比对。由于飞机高度表测高精度在30 m以内，对于地面情报雷达而言，可以将二次雷达的高度数据作为参考标准。

设天线转至方位为β角的位置时，发现一架飞机，一次雷达测定的飞行高度值为H1(β)，二次雷达反馈的高度数据为H2(β)，飞机与雷达天线的斜距为R，则可计算出波束指向仰角偏差值 σθ(β)，即［11］

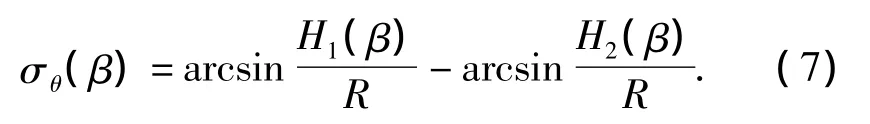
天线转台水平误差引起的波束指向偏差，在以天线为中心的对角线方位上是大小相等、方向相反的。为此要选取若干组对称目标，根据一次雷达测定的高度值和二次雷达反馈的高度数据，利用式(7)计算出波束指向仰角偏差值数据。

例如，计算出 σθ(0°)，σθ(45°)，σθ(90°)，σθ(135°)，σθ(180°)，σθ(225°)，σθ(270°)，σθ(315°)，再计算出这些数据的绝对平均值和对称差值的绝对平均值，令:

若α≈0，说明不存在天线转台水平误差;若α≪1，说明天线转台水平误差比较小。

天线转台水平精度的值也可以初步计算，即

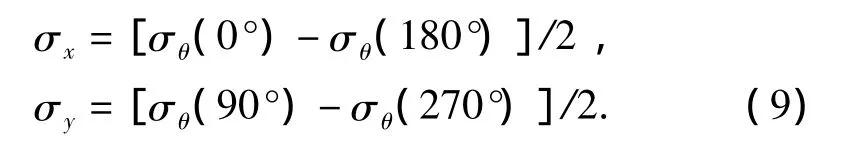
精确的计算要去除阵地反射误差和云雨气象误差的影响。去除阵地反射误差影响的一种方法是参考阵地遮蔽角图，去除云雨气象误差影响的一种方法是选择在阵地周边大范围晴朗天气时实施测定。

4 天线转台水平误差自动修正方案［12］

天线转台水平误差引起波束仰角偏差，由波束仰角偏差引起的测高误差，可通过调整波束仰角指向来消除。调整波束指向在工程上实现起来就是要重新计算一组移相码。技术方案如图6所示。

天线转台水平误差数据σx，σy从天线车调平控制柜中取出，汇流环有空余线路时用有线传输至雷达工作车数据终端。汇流环没空余线路时，设计无线电路，再转用有线传输至雷达工作车数据终端。

5 结束语

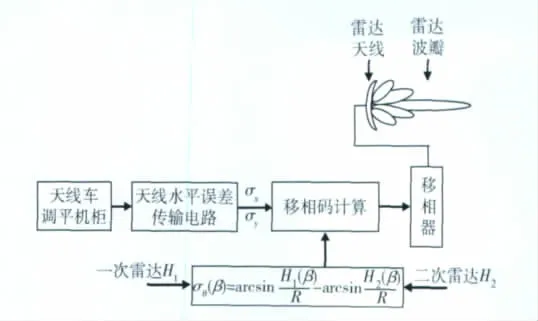
图6 三坐标雷达测高误差自动修正系统Fig.6 3D-radar altimetry definition majorization system

本文对三坐标雷达天线转台倾斜所引起的测高误差所作的分析以及研究提出的修正方法，对于指导部队实施三坐标雷达测高精度阵地优化工作具有现实意义，将对预警探测部队雷达情报质量的提高产生积极影响。同时，对于三坐标雷达生产制造厂家在实施雷达产品性能改进、升级和可靠性增长改造过程中，也具有借鉴意义。

［1］ BARTON D K，WARD H R.Handbook of Radar Measurement［M］.IRE Trans.Artech House，1984:368-369.

［2］ 郦能敬.对空情报雷达的测量精度分析［J］.雷达科学与技术，2005(1):1-10.LI Neng-jing.Measuring Accuracy Analysis of the Air Intelligence Radar［J］.Radar Science and Technology，2005(1):1-10.

［3］ MERRILLS.RadarHandbook［M］.New York:McGRAW-HTLL Publishing Company，1990:215-218.

［4］ 孙国强，田芳宁.雷达测高误差因素分析与修正［J］.理论与方法，2011，30(5):26-28.SUN Guo-qiang，TIAN Fang-ning.Radar Altimeter Error Analysis and Correction Factors［J］.Journal of Theory and Method，2011，30(5):26-28.

［5］ 陈荣虎，黄强辉.相控阵雷达测高误差的修正［J］.电子工程，2007(1):1-9.CHEN Rong-hu，HUANG Qiang-hui.Phased Array Radar Altimeter Error Correction［J］.Journal of Electrical Engineering，2007(1):1-9.

［6］ 陈曦，张中兆，韩帅.大气折射对跟踪天线指向的影响及修正方法［J］.电子测量与仪器学报，2009，23(8):61-66.CHEN Xi，ZHANG Zhong-zhao，HAN Shuai.The Effect of Atmospheric Refraction on Tracking Antenna Pointing and Correction Method［J］.Journal of Electronic Meas-urement and Instrument，2009，23(8):61-66.

［7］ 张光义.相控阵雷达系统［M］.北京:国防工业出版社，1994:221-229.ZHANG Guang-yi.Phased Array Radar System［M］.Beijing:National Defense Industry Press，1994:221-229.

［8］ 束咸荣，何炳发，高铁.相控阵雷达天线［M］.北京:国防工业出版社，2007:176-183.SHU Xian-rong，HE Bing-fa，GAO Tei.Phased Array Radar Antenna［M］.Beijing:National Defense Industry Press，2007:176-183.

［9］ 肖艳姣，刘黎平，杨洪平.区域雷达网同步观测对比分析［J］.气象学报，2007，65(6):920-927.XIAO Yan-jiao，LIU Li-ping，YANG Hong-ping.Synchronous Observation Comparative Analysis of Regional Radar Network［J］.Journal of Climate，2007，65(6):920-927.

［10］ 邵余峰.高机动三坐标雷达比幅测高误差分析及修正［J］.现代雷达，2007，29(4):79-81.SHAO Yu-feng.High Mobile 3D Radar is Higher than Amplitude Measurement Error Analysis and Correction［J］.Modern Radar，2007，29(4):79-81.

［11］ 杨春海.比幅测高误差的自动补偿［J］.现代电子，2002(2):1-5.YANG Chun-hai.Higher than Amplitude Measurement Error Automatic Compensation ［J］.Journal of Modern Electronics，2002(2):1-5.

［12］ 高世超，毕红葵，万洋.探析三坐标雷达测高误差分析及精度提高方法［J］.现代雷达，2009，31(10):25-25.GAO Shi-chao，BI Hong-kui，WAN Yang.Radar Altimeter Error Analysis and the Analysis of Three Coordinates Accuracy Improving Method［J］.Modern Radar，2009，31(10):25-25.