一种新的基于网格聚类的雷达信号预分选算法*

邱磊，杨承志，何佃伟

(空军航空大学，吉林长春 130022)

0 引言

雷达信号分选是电子对抗情报侦察系统的重要组成部分，在当今战场中起着重要作用。近几年，随着雷达信号环境日益复杂，许多学者将数据挖掘技术中的聚类分析方法引入到雷达信号分选领域［1-4］。聚类分选算法可以分为基于划分的聚类算法、基于层次的聚类算法、基于密度的聚类算法、基于网格的聚类以及基于模型的算法等［5-6］。基于网格的聚类算法具有处理速度快、对输入数据顺序不敏感，可以发现任意形状类的优点［7］，是一种有效的信号预分选算法。

现有的基于网格聚类的预分选算法存在的主要问题有:①网格划分数和密度阈值需要人为设定，②聚类边界被当作噪声点丢弃导致聚类精度不高。针对这2个问题，很多学者对算法进行了改进。其中文献［8］提出了先移除孤立点和噪声再进行聚类的方法，但它要计算所有脉冲之间的距离，算法复杂度高，难以满足实时性要求;文献［9］提出了一种动态网格聚类预分选算法，算法复杂度较低，但边界处理效果较差。本文提出了一种新的基于网格聚类的预分选算法。提出了网格数据压缩率概念，首先根据雷达脉冲数和网格数据压缩率，自适应确定网格划分和密度阈值，减少了人为因素的影响;其次利用密度阈值去除孤立点和噪声，对低密度网格进行边界提取，提高聚类精度。

1 一种新的网格聚类预分选算法

1.1 网格聚类概念

给定d维空间D中的一个点，其属性(D1，D2，…，Dd)都是有界的，设第 i维的值在区间［li，hi］中，其中 i=1，2，…，d。则 D=［l1，h1］×［l2，h2］× … ×［ld，hd］。将D的每一维平均分成K个长度相等的区间段。这样将空间D划分为Kd个子空间。若2个网格单元有相邻的边界或顶点，则称这2个网格相交。相交的2个网格互称为邻居。网格单元所包含的数据点的个数称为该网格单元的网格密度。一个网格单元的网格密度大于或等于给定密度阈值MinPts时，称该单元为高密度网格，否则称为低密网格。如果一个低密度网格单元的所有邻居都是低密度单元，那么该单元中的点为噪声。一个聚类是相邻的高密度网格单元的集合。

1.2 算法基本步骤

输入:3维数据集D，数据个数N.

输出:带标号的聚类，噪声点。

(1)读入数据并归一化，归一化公式为x～=(x-xmin)/(xmax-xmin)。xmin表示参数集的最小值，xmax表示参数集的最大值。

(2)自适应计算网格划分数K和网格边长。

(3)将数据映射到的网格，计算网格密度和密度阈值MinPts。

(4)根据MinPts，找出高密度网格和低密度网格，去除空网格;

(5)把每个低密度网格划分成3d个子网格，把有高密度邻居子网格的数据点归为对应的高密度单元，无高密度邻居子网格的数据点作为噪声舍去。

(6)任取一个高密度网格，按照广度优先原则将与之相邻的高密度网格进行合并，重复这个过程直到所有的高密度网格单元处理完毕。

(7)输出聚类结果。

算法流程图如图1所示。

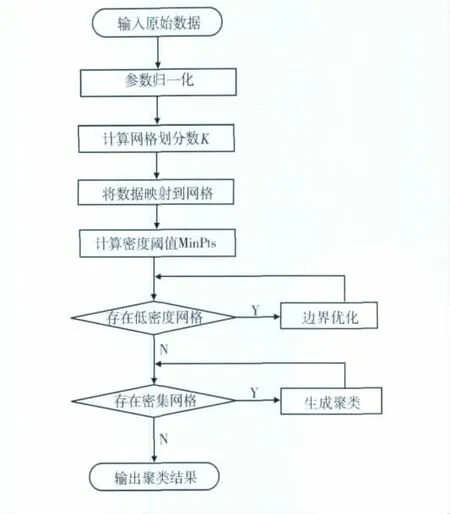
图1 网格聚类算法流程图Fig.1 Flow chart of grid clustering algorithm

1.3 确定网格划分数K

网格划分决定了网格尺寸，对聚类结果有着重要影响。如果网格的尺寸太大，算法会将本属于不同聚类中的点划分到同一个聚类中;如果网格的尺寸太小，网格单元数就多，计算复杂度提高。采用网格划分的方式处理数据本质上是数据压缩，每一维划分数K就代表了数据压缩的程度，本文通过网格数据压缩率来设置参数K，网格数据压缩率α定义为

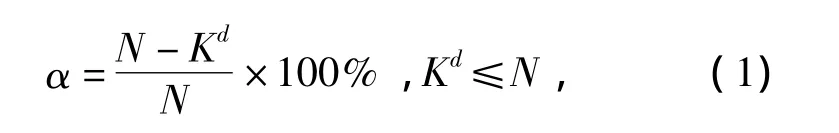
式中:N为输入数据个数;K为网格划分数;d为数据维数。

由式(1)得到网格划分:

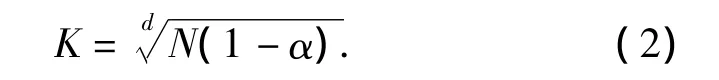
设雷达信号预分选时1 000个脉冲为一帧，α取70%，则

1.4 确定密度阈值MinPts

雷达信号预分选中，密度阈值的作用是滤除混杂在雷达脉冲信号中的噪声脉冲，它的取值与侦察环境中噪声脉冲的数量有关。现有的网格聚类算法要求用户输入密度阈值MinPts来判定网格是否为高密度单元，输入参数的不同可能会导致差别很大的聚类结果［10］。本文根据输入数据和网格划分自动确定密度阈值。依次扫描每个网格单元，得到非空网格的数GridNum，网格的最大密度Max_Grid。N是输入数据个数，则网格密度阈值定义为

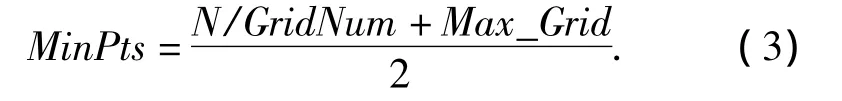
1.5 边界优化

网格聚类预分选中，低密度网格内可能是噪声点或边界点。现有的网格聚类算法直接移除低密度网格，这样低密度网格内的有用信息会被当作噪声点移除，聚类的边界将受到影响。如果把低密度网格中的数据全部归到相邻的高密度网格单元，则又引入了大量的噪声脉冲，还有可能把多部雷达归为一类［11］。本文对低密度网格进行边界提取。首先将低密度网格每一维再等分为3个区间，形成3d子网格单元。把与高密度网格相邻的子网格合并到高密度网格，否则子网格作为孤立点舍去。下面以二维空间为例进行说明。

图2中，数据映射到网格1到网格9。密度阈值MinPts为7，网格4，6，7是高密度网格，其余是低密度网格。可以直观地看出图中存在2部辐射源。记左侧数据点属于辐射源A，右侧数据点属于辐射源B。网格5中包含2部辐射源的边界和噪声脉冲。边界优化时，将网格5每一维三等分，与高密度网格有公共界面的单元归于高密度网格，点a和点b归为网格4，属于辐射源A;点d和点e归为网格6，属于辐射源B;点c是噪声点被移除。可以看出，边界优化处理在正确处理边界点的同时，去除了噪声脉冲，提高了聚类精度。

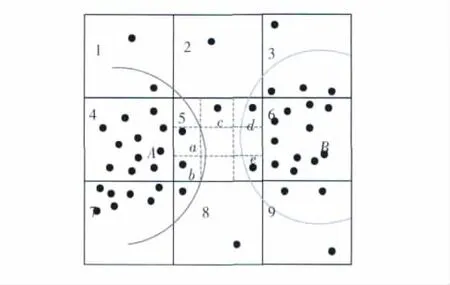
图2 边界优化示例图Fig.2 Edges optimization

2 实验结果及分析

2.1 聚类结果的对比

为了验证本文提出的网格聚类算法用于雷达信号预分选的性能，构造表1的全脉冲数据为进行仿真实验。仿真实验环境为:Windows XP SP3，Intel CPU Q8200@2.33 GHz，3.73 GB内存，编程工具为Matlab R2008a。

表1中的7部雷达按照到达时间顺序混叠在一起，考虑到实际信号产生时的参数与预设总有一定误差，以及传输信道影响和接收机的测量误差，对每个参数都加上了一个随抖动，其中到达方向(direction of arrival，DOA)的偏差是 2°，载频(radio frequency，RF)和脉宽(pulse width，PW)的偏差都在1%以内。同时加入了10%的环境噪声［12］。从图3可以看出，噪声与7部雷达信号在到时域空域和载频域都是严重交叠的。基本满足复杂电磁环境的要求。

输入脉冲总数为 870个，α =0.7，K=7，MinPts=3。仿真结果的二维分布如图4所示。由图4可以看出，网格聚类算法将含有噪声的全脉冲数据正确聚为7类，且较好地去除了散落在真实脉冲参数值范围之外的脉冲，即去除了大部分噪声脉冲，实验结果验证了网格聚类算法的有效性。表2给出了分选结果统计。

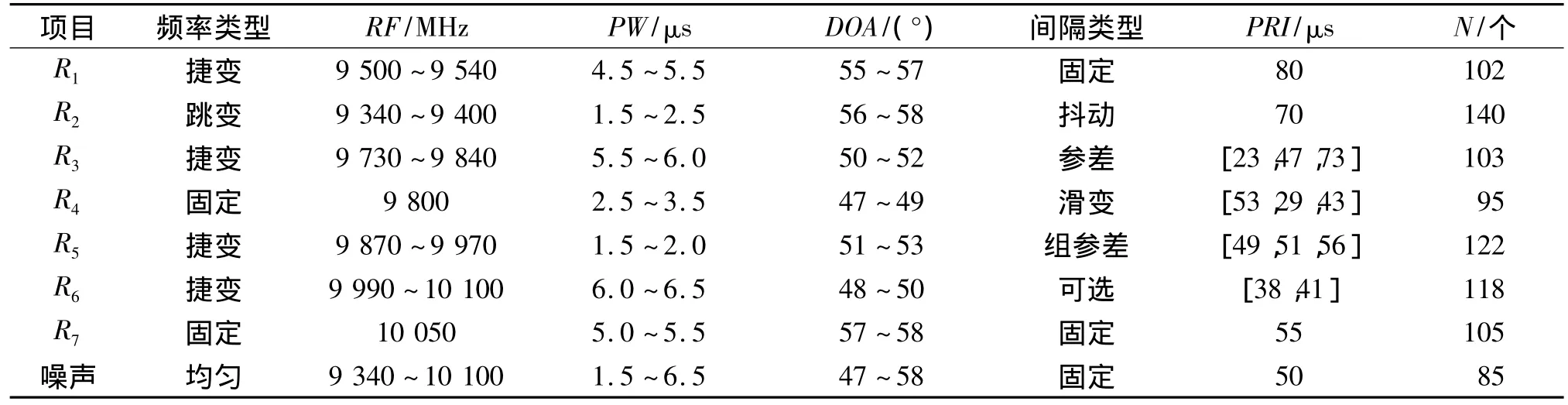
表1 雷达参数仿真数据Table 1 Simulation data of radar parameters

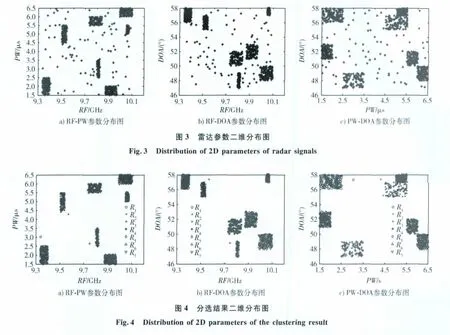
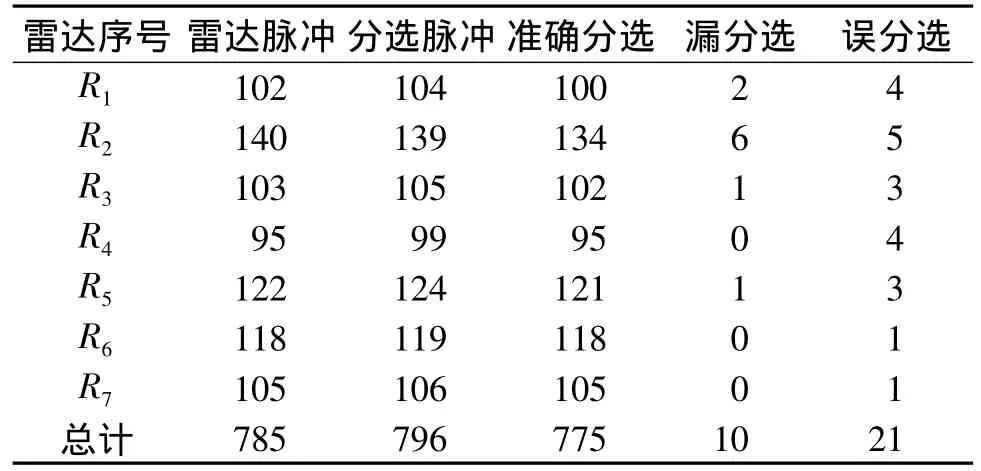
表2 分选结果信息表Table 2 Information of sorting result

误分选是把本不属于此雷达的脉冲归到该雷达中，漏分选是指本属于该雷达的脉冲没有被划分到该类中。对于雷达信号预分选而言，漏分选比误分选严重得多。

表2中参与分选的全脉冲总数为870个，其中包括噪声脉冲85个，真实脉冲785个。从表2得到，网格聚类分选得到脉冲796个，其中准确分选775个，漏分选10个，误分选21个。

表3给出了相同实验条件下，α取不同值时的仿真结果，其中α＇是实际的压缩率。

表3 不同网格数据压缩率下的分选结果信息表Table 3 Information of sorting result with different grid data compression ratios

网格数据压缩率决定了网格划分，α=0.3即压缩率是30%时，由于网格划分只能取整数，K=9，总的网格数为729。平均每个网格内有870/729=1.193 4个数据点，因此实际的压缩率只有16.21%。

从表3可以看出，压缩率为70%时，噪声条件下分选结果和运行时间明显优于其他2个压缩率条件下的结果。这是由于随着α的增大，网格划分数减少，运行时间减少，每个网格内包含的数据点增多，同一部辐射源信号容易落入同一个网格，使得大部分信号都包含在网格中。同时算法对网格边界进行优化处理，减少了漏脉冲数。在某些网格划分下，同一个聚类中的数据可能分散到多个相邻的网格中，而这些网格不一定都是高密度网格，边界优化使得一部分有效数据被舍弃。这也是α=0.5时的分选结果差于α=0.3时的原因。因此，在本实验条件下，α=0.7时，算法运行时间短，分选准确率高，网格聚类的优势得以体现。而当α取值较小时，划分的网格数与输入数据点数相当，体现不出网格聚类的优势。

将本文提出的方法与文献［8］的网格密度聚类和文献［9］的移动网格聚类进行对比，α=0.7。相同实验条件下，算法的分选结果如表4所示。

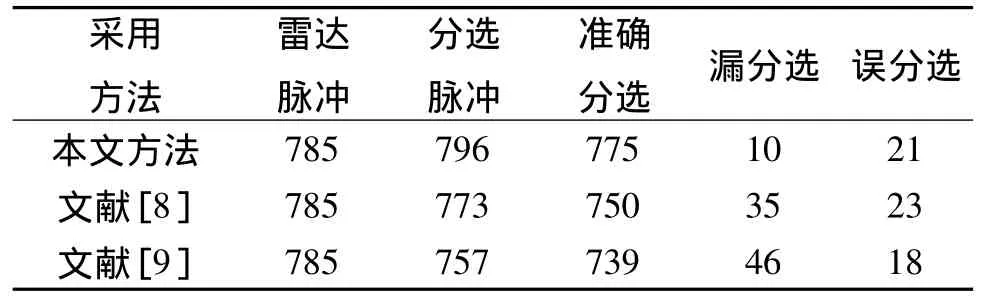
表4 3种聚类方法预分选结果比较Table 4 Comparison of pre-sorting results by three clustering algorithms

从表4的分选结果可看出，在相同数据源和仿真条件下，采用本文得到的漏脉冲数目明显小于另外2种方法。这是由于本文对边界进行了处理，误分选脉冲数和另外2种方法相似，略优于文献［9］中的方法。在噪声脉冲较多时，误分选数增大，但是漏分选数较小。实验结果说明，本文的网格聚类算法比现有的聚类算法有较高的性能，对噪声脉冲有良好的识别能力。

2.2 算法复杂度分析

网格聚类算法的计算复杂度为O(N+Kd+3d)［11］，其中，d为数据空间的维数，N为雷达脉冲总数，Kd为划分的网格数。对于雷达信号预分选，采用了RF，PW，DOA 3位参数，因此 d=3，且 Kd＜N。由此可知，网格聚类算法在处理三维数据时，算法的计算复杂度在数据对象总数较大的情况下趋近于O(n)。因此，网格聚类算法能够较好地满足雷达信号预分选实时性的需要。

3 结束语

本文提出了一种新的网格聚类算法，并将该算法应用于雷达信号预分选领域。算法复杂度低，可扩展性好，可以发现任意形状的聚类，适合大规模的侦察数据集，对噪声脉冲也有很好的识别能力，较好地满足雷达信号预分选的要求。

［1］ 叶菲，罗景青.基于BFSN聚类的雷达信号分选与特征提取算法［J］.舰船电子对抗，2005，28(3):29-34 YE Fei，LUO Jing-qing.Radar Signal Sorting and Feature Extraction Algorithm Based on BFSN Clustering［J］.Shipboard Electronic Countermeasure，2005，28(3):29-34.

［2］ 郭杰，陈军文.一种处理未知雷达信号的聚类分选方法［J］. 系统工程与电子技术，2006，28(6):853-856.GUO Jie，CHEN Jun-wen.Clustering Approach for Deinterleaving Unknown Radar Signals［J］.Systems Engineering and Electronics，2006，28(6):853-856.

［3］ 张红昌，阮怀林，龚亮亮，等.一种新的未知雷达辐射源聚类分选方法［J］.计算机工程与应用，2008，44(27):200-202.ZHANG Hong-chang，RUAN Huai-lin，GONG Liang-liang，et al.New Clustering Approach for Sorting Unknown Radar Emitter Signal［J］.Computer Engineering and Applicaitons，2008，44(27):200-202.

［4］ 岳宏伟，罗景青，吕久明，等.雷达信号非均匀粒度聚类分选方法［J］.火力与指挥控制，2008，33(8):23-26.YUE Hong-wei，LUO Jing-qing，LÜ Jiu-ming，et al.Research on Radar Signal Sorting Method Based on Uneven Granules Clustering［J］.Fire Control and Command Control，2008，33(8):23-26.

［5］ 赵慧，刘希玉，崔海青.网格聚类算法［J］.计算机技术与发展，2010，20(9):83-85.ZHAO Hui，LIU Xi-yu，CUI Hai-qing.Grid-Based Clustering Algorithm［J］.Computer Technology and Development，2010，20(9):83-85.

［6］ 程伟想.网格聚类算法的研究［D］.保定:华北电力大学，2008:9-11.CHENG Wei-xiang.Research of Grid-Based Clustering Algorithm［D］.Baoding:North China Elertic Power U-niversity，2008:9-11.

［7］ 邱保志，郑智杰.基于局部密度和动态生成网格的聚类算法［J］.计算机工程与设计，2010，31(2):385-387.QIU Bao-zhi，ZHENG Zhi-jie.Grid Clustering Algorithm Based on Local Density and Dynamic Creating Grids［J］.Computer Engineering and Design，2010，31(2):385-387.

［8］ 向娴，汤建龙.一种基于网格密度聚类的雷达信号分选［J］.火控雷达技术，2010，39(4):67-72.XIANG Xian，TANG Jian-long.A Method of Radar Signal Sorting Based on Grid Density Clustering［J］.Frie Control Radar Technology，2010，39(4):67-72.

［9］ 何佃伟，杨承志，张荣，等.一种基于改进网格聚类的雷达信号分选算法［J］.雷达与对抗，2011，31(2):43-49.HE Dian-wei，YANG Cheng-zhi，ZHANG Rong，et al.A Radar Signal Sorting Algorithm Based on Improved Grid Clustering［J］.Radar ＆ ECM，2011，31(2):43-49.

［10］ 邱保志，刘洋，陈本华.基于网格熵的边界点检测算法［J］. 计算机应用，2008，28(3):21-24.QIU Bao-zhi，LIU Yang，CHEN Ben-hua.Grid-Entropy Based Boundary Points Detecting Algorithm ［J］.Computer Applications，2008，28(3):21-24.

［11］ 邱保志，沈钧毅.基于网格技术的高精度聚类算法［J］.计算机工程，2006，32(3):12-13.QIU Bao-zhi，SHEN Jun-yi.A Grid-Based Improving Clustering Quality Algorithm［J］.Computer Engineering，2006，32(3):12-13.

［12］ 孙连宝，刘治国.雷达侦察信号环境描述与建模［J］.舰船电子工程，2009，29(11):93-95.SUN Lian-bao，LIU Zhi-guo.Description and Modeling of the Radar Reconnaissance Signals Environment［J］.Ship Electronic Engineering，2009，29(11):93-95.