基于突防网格模型的动态航迹规划*

孙利军

(光电信息控制和安全技术重点实验室，河北三河 065201)

0 引言

随着现代科技的快速发展，低空飞行受到越来越多的重视。为了提高低空飞行的生存概率和作战效果，需要制定一个综合的规划系统进行任务规划、资源协调和确定飞行航路［1］。其中航迹规划为重要组成部分，它的目的就是在最短的时间内，面对复杂的地形、地貌、障碍、威胁等因素进行快速、有效地规划，实现安全航行，到达目标［2-3］。对于航迹规划的具体方法本文查阅了许多资料，分析比较了动态规划法、梯度法、神经网络、专家系统和遗传算法等［4-5］，由于动态规划算法最适合解决动态全局最优问题，在具体的程序实现中并没有发现“维数爆炸”的问题［6］，所以最终方案是将动态规划算法用于节点间的分段航迹规划，继而进行航迹合并、航迹选择与评估，并给出了最优的规划结果，经仿真验证了该方法能够快速、有效地完成低空航迹规划任务。

1 动态航迹规划方法

1.1 突防网格模型

以数字地形高程模型为基础，将该数字地图划分为具有离散梯度值的网格单元［1］，形成分区网格，每个网格的成本值即为该网格内的平均地形梯度值。

在分区网格的基础上，一方面考虑地形的山峰障碍威胁，将山峰的高程值大于一定值的区域设为禁飞区，即该处的网格概率值设为1。另一方面考虑攻击威胁，根据攻击区中心坐标和区域半径所对应的网格区域中，将杀伤力指标合并到对应的网格概率值中［7］。经过这两方面的处理，将山峰障碍威胁、攻击威胁一并数字化在分区网格上，这样就形成了突防网格模型，每个网格的成本值即为该处的飞行突防概率值。这样建立的突防网格模型是综合了地形、攻击威胁、山峰障碍等因素为一体的飞行模型，以此为基础规划的飞行航迹能够绕过山峰障碍和威胁区以最低的坠毁概率安全飞行。因此突防网格模型是航迹规划系统的环境数据基础。

1.2 基本航迹区、导航点的选择以及匹配导航

基本航迹区通常是包括目标点在内的一片导航基准地图，常用的有地形匹配区［8］和景象匹配区［8］。导航点是导航基准地图上的一些小区域，导航点相应地有地形匹配点和景象匹配点。地形匹配点的选择依据地形的高度和梯度，在导航区基准图上，计算选择高度在一定高度以下，绵延起伏的丘陵地区中的特征点作为地形匹配点。景象匹配点常常选定那些特征明显，独立像元数较大的区域作为景象匹配点。

在低空飞行中地形匹配区通常采用地形断线扫描匹配，通过高度及梯度计算找到导航基准图中的地形匹配点，以进行地形导航的实时修正。飞行器在景象匹配区采用图像方差匹配方法，在拍摄到的实时景象图片后，通过与库存的基准图的统计方差计算找到相应的景象匹配点，以完成景象匹配导航的实时修正。

1.3 动态规划算法原理

在航迹规划中，用节点的概念来涵盖包括起始点、各个地形匹配点、各个景象匹配点、目标点在内的航迹必须经过的所有约束点。在2个相邻节点之间进行的航迹规划方法是整个航迹规划的基础，本文选用动态规划算法［9-10］用于节点间的航迹规划。

在由穷举法求A0至Am之间最短路径的问题上，对于任一节点 Pk(i，j)，i与 j之间有多条路径，如图1所示。

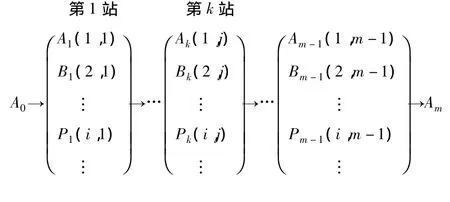
图1 A0至Am之间最短路径问题Fig.1 Shortest path problem of A0and Am

可以得出最短路径问题的这样一个特性:如果A0至Am之间最短路径的第k站通过Pk，则这一最短路径在由Pk出发到达终点Am的那一部分路径，对于始点为Pk到达终点的所有可能的路径来说，必定也是距离最短的。根据这一特性，可以把一个最短路径问题转化为多段判决问题来解决。

设 d(i，j，k)为从 i与 j的最短路径，k 为最短路径经过的第k站，得到递归公式如下:

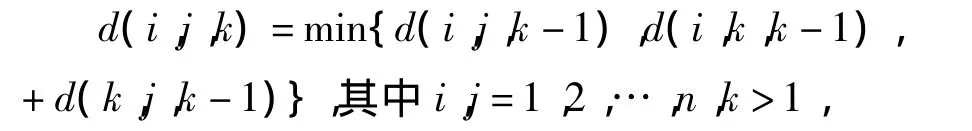
算法如下:

以上为动态规划的算法原理，在运用该方法解决具体问题的时候，将最短距离替换以具体的目标要素，即可解决具体的各种实际问题，本文用该算法解决航迹规划问题的原理如下所述。

1.4 基于动态规划的航迹规划方法

图2中的表格为某一区域建立的突防网格模型图中的一部分，表格中数值为各点的突防概率初始值，由终止节点到起始节点逆向搜索［11］，根据动态规划算法计算图上各点所走航路的突防概率过程值见图3。根据图3的计算结果，确定出航迹路线，如图3中箭头线所示。在航迹规划之后，即可得出2节点间的总的飞越成本，也就是这2个节点之间所经航路的突防概率过程值的总和，将其保存以备作进一步的处理。

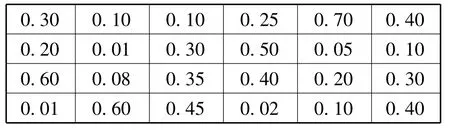
图2 突防概率初始值Fig.2 Initial probability of penetration

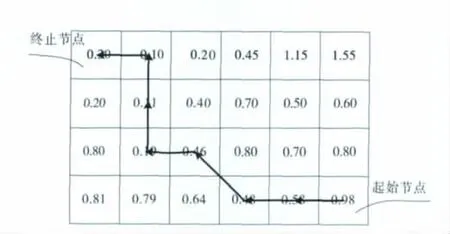
图3 突防概率过程值及航迹规划结果Fig.3 Process probability of penetration＆the result of trajectory planning

1.5 航迹合并

这一过程是将相应的分段航迹连接成一条近似完整的航迹线。每一个起始点可以到达许多导航点，最终到达目标点，这样产生的航迹表现为树形，称为航迹树。这棵航迹树包括了起始点和它所能到达的每个匹配点经规划后的航迹路线，将这棵航迹树每条航迹线的飞越成本计算得出并存储以备使用。

为了作简洁说明和减少航线的数目，暂不考虑起始点和目标点，在突防网格模型图4中，选定的第1地形匹配区的匹配点为M1与M2，第2地形匹配区的匹配点为M3与M4，第3地形匹配区的匹配点为M5与M6，第1景象匹配区的匹配点为V1与V2，第2景象匹配区的匹配点为V3与V4，第3景象匹配区的匹配点为V5与V6。

从图中可清楚地看出，经过每个匹配节点的航迹线均为32条，从起始节点M1与M2开始计算出连接目标点的节点V5与V6的每条航线的飞越成本，并储存以备下一步使用。

1.6 航迹评估

航迹选择实质上就是在每个匹配区选择最佳匹配点的过程，在上面航迹合并的基础上，计算连接起始点到航迹树的每条航迹路线，再由每条航迹路线到达目标点的总的飞越成本，选择具有最低飞越成本值的路径，即为最佳航迹路线。

图4 航迹合并Fig.4 Trajectory merge

在图4中，从目标点开始反向搜索，分别计算到达景象匹配节点V5和V6的飞越成本，选择两者中具有最低飞越成本的节点，如图4中加粗航线所经的V5，然后根据上述航迹合并中所计算储存好的经过V5的每条航线的飞越成本中，选择具有最低飞越成本的航迹，图4中V5至M2之间加粗的航线，也就是其间的最佳航迹。从M2开始至起始点之间仍然是动态规划反向搜索，直至起始点为止，这样规划完成的一条完整航迹线即为从起始点到目标点之间最终选择出的最优航迹，如图4中所示的加粗线即为最优的参考航迹。

由一系列具体的规划方法生成一条最优的参考航迹，但是在实际的飞行中并非一定严格按照参考航迹来飞，它还要受到自身约束条件(例如:飞行高度、飞行速度、最小转弯半径、滚转角等)的限制。因此生成参考航迹后还要根据飞行器自身的性能指标对参考航迹进行局部优化［12］，最后生成最优航迹。

2 仿真结果及分析

2.1 突防网格模型的建立

根据上面介绍的低空动态规划方法，本文以某一区域数字地图为基础数据，形成了突防网格模型，然后选择地形匹配区和景象匹配区及相应的地形匹配点和景象匹配点，建立了基于动态规划算法为分段航迹规划的应用程序，并通过航迹段合并及航迹选择和评估，最后得到最优的参考航迹路线结果。

在本航迹规划系统中，可随时根据攻击区变化的情况，将最新的内容读入程序，在程序执行之中，即将攻击威胁数字转化在突防网格模型图上，如图5所示为突防网格模型图，其中A，B，C为3个攻击区，其具体内容如下:

A区:攻击武器为导弹，

攻击半径在内圆范围内杀伤力为70%，

攻击半径在外圆范围内杀伤力为30%;

B区:攻击武器为高炮，

攻击半径在内圆范围内杀伤力为70%，

攻击半径在外圆范围内杀伤力为30%;

C区:攻击武器为导弹，

攻击半径在内圆范围内杀伤力为70%，

攻击半径在外圆范围内杀伤力为30%。

根据上述匹配区及匹配点的选择原则，最终的选择结果如图5所示，靠近起始点Start为3个地形匹配区，每个地形匹配区内有2个地形匹配点(图中标以M的点)，在靠近目标点Target为3个景象匹配区，每个景象匹配区内有2个景象匹配点(图中标以V的点)。

2.2 最优参考航迹结果及分析

由任务规划系统选定的起始点、3个地形匹配区、3个景象匹配区、目标点等信息，根据本文建立的航迹规划系统经过分段航迹规划、航迹合并、航迹选择与评估得出最终的航迹规划结果。图5为在突防网格模型基础上的航迹规划系统完成的最优参考航迹结果，以红色线表示。

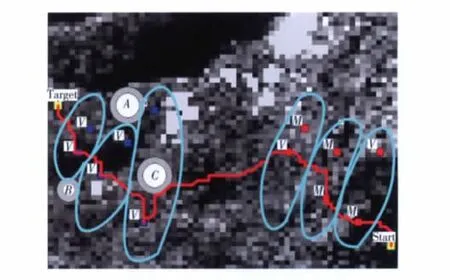
图5 最优参考航迹结果Fig.5 Optimal result of trajectory planning

可以看到，在突防网格模型图上从起始点开始最优航迹线基本走突防概率低的网格(深色)，并能安全地绕过山峰障碍以及攻击威胁区，安全到达目的地。经过改变包括起始点和目标点在内的节点坐标反复试验，验证了本文建立的航迹规划方法能够快速、有效地实现低空航行任务，具有很好的实用性。

3 结束语

本文建立了基于突防网格模型的航迹规划系统，将动态规划算法应用于分段航迹规划方法中，然后通过航迹合并及航迹评估，最后得到最优的参考航迹路线结果。经仿真试验证明该系统不仅能够回避已知的威胁、山峰障碍，而且能够实时接收指控系统的指令，根据实际情况重新规划航迹，回避突然来袭的威胁，最终安全完成低空飞行任务。

［1］ 叶文，廉华耕，漆云海，等.无人机航路算法研究［J］.电光与控制，2011，18(2):8-13.YE Wen，LIAN Hua-geng，QI Yun-hai，et al.Path Planning Algorithm for UAV［J］.Electronics Optics＆ Control，2011，18(2):8-12.

［2］ Myron Hura，Gary Mcleod.低可观测性飞机和巡航导弹的航迹规划问题［J］.徐海江，编译.飞航导弹，1997(5):17-23 Myron Hura，Gary Mcleod.Trajectory Planning of Low Observable Aircraft and Cruise Missile［J］.XU Haijiang，Translated.Winged Missiles Journal，1997(5):17-23.

［3］ Myron Hura，Gary Mcleod.低可观测性飞机和巡航导弹的航迹规划问题(续)［J］.徐海江，编译.飞航导弹，1997(6):3-9.Myron Hura，Gary Mcleod.Trajectory Planning of Low Observable Aircraft and Cruise Missile［J］.XU Haijiang，Translated.Winged Missiles Journal，1997(6):3-9.

［4］ 袁卫东.一种新的综合TF/TA最优航迹算法［J］.南京航空航天大学学报，1996，28(4):481-486.YUAN Wei-dong.A New Optimal Trajectory Planning of Comprehensive TF/TA［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，1996，28(4):481-486.

［5］ 赵锋，杨伟，王伟，等.基于组合优化算法的无人机航迹规划方法研究［J］.弹箭与制导学报，2009，29(2):282-285.ZHAO Feng，YANG Wei，WANG Wei，et al.A Study of UAV Trajectory Planning Approach Based on Combined Optimization Method［J］.Journal of Projectiles，Rockets，Missile ＆ Guidance，2009，29(2):282-285.

［6］ 高晖，陈欣，夏云程.无人机航路规划研究［J］.南京航空航天大学学报，2001，33(2):135-138.GAO Hui，CHEN Xin，XIA Yun-cheng.Study on Trajectory Plan for Unmanned Aircraft Vehicle［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2001，33(2):135-138.

［7］ 徐克虎，贺也平，沈春林.一种改进的地形轮廓预测匹配辅助导航算法［J］.航空计算技术，2000，30(1):9-11.XU Ke-hu，HE Ye-ping，SHEN Chun-lin.A Improved Algorithmic of Terrain Contour Forecast Matching Aided Navigation［J］.Aeronautical Computing Technique，2000，30(1):9-11.

［8］ 李跃.导航与定位［M］.北京:国防工业出版社，2008:433-446.LI Yue.Navigation and Positioning［M］.Beijing:National Defense Industry Press，2008:433-446.

［9］ 卢开澄.单目标、多目标与整数规划［M］.北京:清华大学出版社，1999.LU Kai-cheng.Single Objective and Multiple Objectives Programming［M］.Beijing:Tsinghua University Press，1999.

［10］ 罗伯特约翰.动态规划原理［M］.陈伟基，译.北京:清华大学出版社，1984.Robert John.The Principle of Dynamic Programming［M］.CHEN Wei-ji，Translated.Beijing:Tsinghua University Press，1984.

［11］ 吴剑，喻玉华，周继强，等.无人机航路规划中的变步长 A*算法［J］.电光与控制，2011，18(5):1-6.WU Jian，YU Yu-hua，ZHOU Ji-qiang，et al.Path Planning Algorithm of the Variable Step A*for UAV［J］.E-lectronics Optics ＆ Control，2011，18(5):1-6.

［12］ 闵昌万，袁建平.航迹规划中安全走廊及参考轨迹的确定［J］.飞行力学，1999，17(2):12-16.MIN Chang-wan，YUAN Jian-ping.The Determination of Safe Corridor and Reference Path in Route Planning［J］.Flight Dynamics，1999，17(2):12-16.