要地防空作战雷达干扰任务分配模型研究*

傅从义，何俊，王斌

(电子工程学院，安徽合肥 230037)

0 引言

信息化条件下的要地防空作战中，来袭目标较多，我方的干扰站数量有限，干扰站分配是否合理，已成为直接影响雷达干扰效果的重要因素之一。因此，如何合理为干扰站分配干扰目标，以取得最佳或满意的整体干扰效果是急需解决的问题。这是一个典型的组合优化问题，并且是一个非确定多项式(non deterministic polynomical，NP)难题，其可能的组合方案与待分配的干扰站数目是成指数型增长的，所以一般很难精确求其最优解。而遗传算法［1-2］通过模拟自然进化过程搜索最优解，能有效解决该问题。同时，对干扰效果的评估也很难精确得到。因此，本文尝试采用模糊综合评判和改进的遗传算法对要地防空作战雷达干扰任务分配问题进行研究。

1 要地防空作战雷达干扰任务分配的典型情况分析及处理

要地防空作战中的雷达干扰任务分配一般分为3种情况:干扰站数量与雷达数量相等;干扰站数量大于雷达数量;干扰站数量小于雷达数量。针对这3种情况，本文提出了对目标雷达进行整合和增加虚拟干扰站及虚拟雷达的方式进行处理。具体情况如下:

(1)干扰站数量等于雷达数量

当干扰站的数量与雷达的数量相等时，可直接进行任务分配，确保一部干扰站干扰一部雷达，这是典型的一对一分配。

(2)干扰站数量多于雷达数量

当干扰站数量多于雷达数量时，可先增加一定数量的虚拟雷达，使雷达和干扰站的数量相等，形成典型的一对一分配问题再进行求解。此时，规定各干扰站对增加的虚拟雷达的干扰效益为0。任务分配结束以后，可视情况将分配给虚拟雷达的干扰站重新分配，加强对雷达的干扰效果。

(3)干扰站数量少于雷达数量

当干扰站数量少于雷达数量时，先从时域、空域和频域三维角度出发，对来袭飞机的雷达进行整合，得到能同时干扰的雷达集合。若整合后雷达数量仍大于干扰站数量，则增加一定数量的虚拟干扰站，对雷达和干扰站进行一对一的分配。

目标雷达整合需要用到大量专家知识和经验。一般是基于以下3个原则进行整合［3］:

(1)时间一致

时间一致是目标雷达整合的前提，只有威胁时间相同时，才可能用一部干扰站同时对其进行干扰。

(2)空间一致

若2部雷达位置相距甚远，不在一部干扰站作用范围之内，或者雷达的辐射空间、方向不一致，则不能用一部干扰站同时进行主瓣干扰。

(3)频段一致

对于时间和空间都大致重合的2部雷达，若它们的工作频段不一致，或者其并集已超过一部雷达干扰站的频段范围，则无法用一部干扰站进行有效干扰。

2 要地防空作战雷达干扰任务分配战术计算模型

2.1 雷达干扰效果评估矩阵

干扰站对雷达的干扰效益是进行干扰任务分配的主要依据。干扰效益是由干扰效果和目标雷达的威胁度共同决定的。这里主要给出雷达干扰效果的详细计算过程，目标雷达威胁度的计算另行讨论。

雷达干扰任务分配是一个复杂的过程，这里采用模糊综合评判法对干扰效果进行评估。

2.1.1 雷达干扰效果评估指标

为了准确地评估干扰站对目标雷达的干扰效果，评估指标的选取至关重要。一般情况下，在评估干扰站对雷达的干扰效果时，主要考虑以下4个因素［4-6］:

(1)干扰频率

干扰站要在频率、方向和极化上都对准敌方雷达，才能使施放的干扰有效。频率对准、方向对准和极化对准是干扰信号进入敌方雷达接收机的必要条件［7］。

(2)干扰功率

干扰站的干扰功率要足够大，即雷达接收到的干扰功率与回波功率之比应大于雷达正常接收信号时必需的干扰信号与回波信号的最小功率之比，干扰才能有效。

(3)干扰时机

干扰时间要合适，要在雷达的威胁时间里进行有效干扰。

(4)干扰样式

干扰站的干扰样式要和雷达的技术体制相匹配。雷达的技术体制不同，其接收信号的处理方法和雷达的工作方式也不同。因此，要提高干扰效果，应针对不同技术体制的雷达，选用不同的干扰样式［8］。

本文选取干扰频率、干扰功率、干扰时机、干扰样式4个因素作为评估指标。

2.1.2 评估指标的隶属度函数

(1)干扰频率的隶属度函数

对于干扰频率，可以用频率瞄准效益函数Ef来评估。频率瞄准效益函数表示干扰站对雷达的频率瞄准程度对干扰效果的影响。Ef的计算有2种情况:

1)干扰单部雷达

假设干扰站的工作频率范围为［fJmin，fJmax］，单部雷达的工作频率范围为［fRmin，fRmax］，则可得到频率瞄准效益函数Ef的计算公式:

2)干扰单个雷达组

干扰单个雷达组时，记单个雷达组中雷达数为lR部，因此，整个雷达组的工作频率范围［f'Rmin，f'Rmax］是该雷达组中所有雷达工作频率的并集，即有:

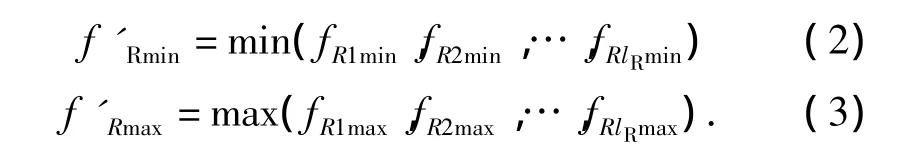
得到单个雷达组的工作频率范围后，用其替换单部雷达的工作频率范围，可得到类似式(1)的频率瞄准效益函数。频率瞄准效益函数值越大，进入雷达接收机的干扰能量相对较多，干扰效果就越好。

(2)干扰功率的隶属度函数

对于干扰功率，可用功率压制效益函数Ep来评估干扰站对雷达的干扰效果。功率压制效益函数表示干扰站对雷达的功率压制程度对干扰效果的影响。Ep的计算有2种情况:

1)干扰单部雷达

干扰单部雷达时，Ep可用下式进行计算:

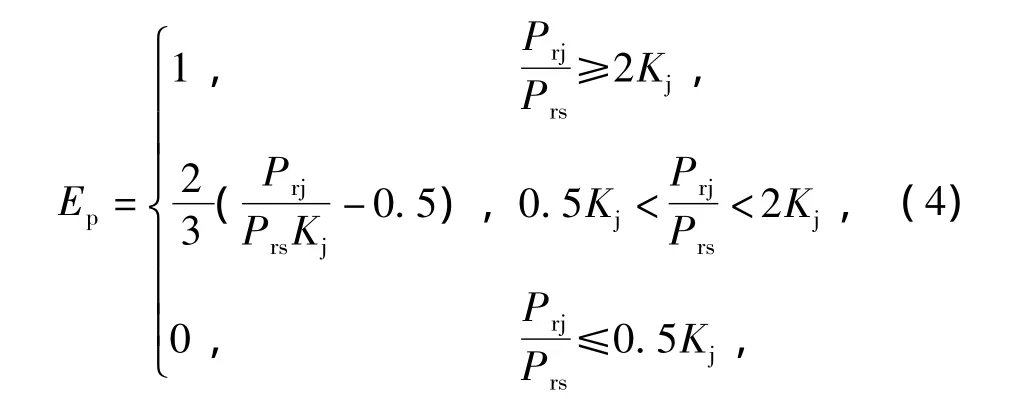
式中:Prj为单部雷达接收到的干扰功率;Prs为单部雷达接收到的目标回波信号功率;Kj为单部雷达正常工作所必需的最小干信比。

2)干扰单个雷达组

干扰单个雷达组时，Ep可用式(5)进行计算:

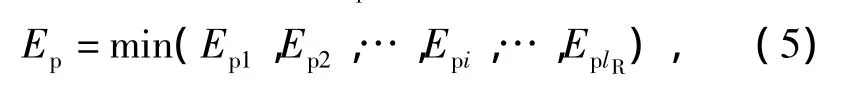
式中:Epi为干扰单个雷达组中第i部雷达时的功率压制效益函数，i∈［1，lR］;

类似式(4)，可得Epi的计算公式:

式中:Prji为单个雷达组中的第i部雷达接收到的干扰功率;Prsi为单个雷达组中的第i部雷达接收到的目标回波信号功率;Kji为单个雷达组中的第i部雷达正常工作所必需的最小干信比。

(3)干扰时机的隶属度函数

对于干扰时机，可用压制时间效益函数Et来评估干扰效果。压制时间效益函数表示在雷达的威胁时间里，干扰站对雷达能有效压制的时间段对整体干扰效果的影响程度。Et的计算有2种情况:

1)干扰单部雷达

假设雷达的威胁时间段为［tRmin，tRmax］，实施有效干扰的时间段为［tJ1，tJ2］。在不同时刻，干扰站对雷达的干扰压制情况对整体干扰效果影响程度不一样。于是，可以用一个非线性分段函数来进行拟合。根据实际情况，将整个雷达威胁时间段［tRmin，tRmax］分成N段。首先，确定各段的压制时间效益值Eti，然后综合各段的效益值来确定压制时间效益值Et。即:

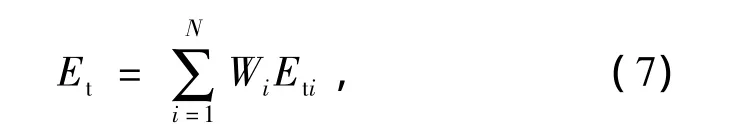
式中:Wi为第i段的权重，且满足归一化要求，即:

2)干扰单个雷达组

干扰单个雷达组时，整个雷达组的威胁时间段［t'Rmin，t'Rmax］是该雷达组中所有雷达威胁时间的并集，即有:

在得到单个雷达组的威胁时间段后，将该时间段分成若干段，再利用式(7)，可计算得出Et。

(4)干扰样式的隶属度函数

对于干扰样式，可用干扰样式效益因子Eg来评估干扰效果。干扰样式效益因子表示干扰站选择的干扰样式对干扰效果的影响程度。

干扰样式必须与雷达技术体制相匹配，才能取得较好的干扰效果。不同干扰样式对不同技术体制雷达的干扰效益因子，由雷达对抗专家确定。Eg的值可以用0，1之间的数表示。Eg取值越大，说明所选的干扰样式对当前雷达的干扰效果越好。

2.1.3 雷达干扰效果评估矩阵

设有m部干扰站，n部目标雷达，根据隶属度函数分别计算出m部干扰站分别对第j部雷达Rj的干扰效果，相应的隶属度矩阵记为

式中:矩阵Ej中每一行的向量为各部干扰站对第j部雷达在该指标下的干扰效果评估值;每一列向量为第i部干扰站对第j部雷达在各个评估指标下的干扰效果评估值。

这里用层次分析法(analytic hierarchy process，AHP)确定各指标的权重，其具体步骤可参考文献［9］的有关内容。记权重为

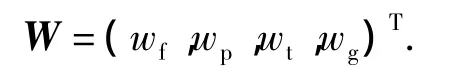
进行模糊综合评判时，需要综合考虑所有指标对模型的影响，故采用加权平均型模型M(·，+)。

计算第i部干扰站对第j部雷达的综合干扰效果评估向量:

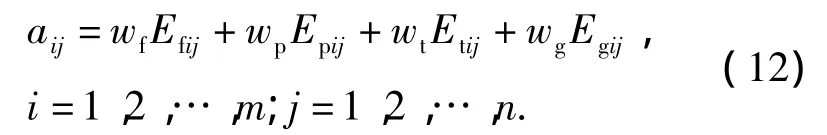
得到雷达干扰效果评估矩阵

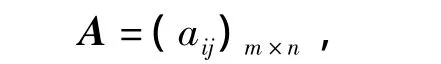
式中:aij为干扰站Ji对雷达Rj的综合干扰效果评估值。

2.2 雷达干扰任务分配模型

假定现有m部干扰站，n部雷达目标(包括雷达组)。根据2.1的雷达干扰效果评估矩阵，可建立要地防空作战雷达干扰任务分配模型，进行干扰站与雷达的任务分配，以使总干扰效益值达到最大。

雷达干扰任务分配的目标函数为

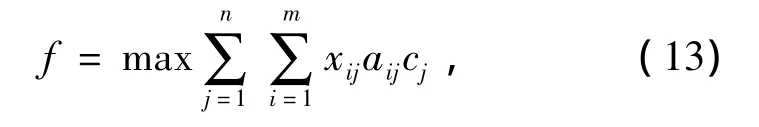
约束条件为

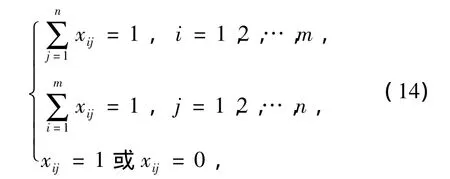
式中:xij为决策变量，xij=1，表示第i部干扰站Ji对第j部雷达Rj进行干扰;xij=0，表示第i部干扰站Ji不对第j部雷达Rj进行干扰。aij为雷达干扰效果评估矩阵A中第i部干扰站Ji对第j部雷达Rj的干扰效果值;cj为第 j(j=1，2，…，n)部雷达 Rj的威胁度评估值(此处不讨论其具体计算方法)。

3 基于遗传算法的模型求解

本文对遗传算法进行改进，并采用改进的遗传算法对所建的要地防空作战雷达干扰任务分配模型进行求解［10-12］。

改进遗传算法的具体情况如下:

(1)编码方法

对于要地防空作战雷达干扰任务分配问题而言，采用二进制编码时，虽然染色体的长度随着干扰站和雷达的增多急剧增长，但计算染色体适应度时可省去解码的麻烦，而且对于最优染色体，只需将其转换为m×n的矩阵。因此，决策变量采用二进制编码方式。

(2)适应度函数

染色体的适应度函数为

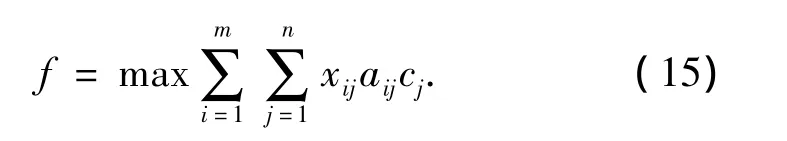
同时，要满足约束条件的限制。否则施加惩罚，令染色体适应值为0(或一个极小数)。

(3)选择

这里采用最佳保留方法。

(4)交叉

交叉操作是遗传算法中最主要的遗传操作。鉴于任务分配的编码设计，采用均匀交叉的策略。

(5)变异

这里选择非均匀变异，算子按式(16)进行。

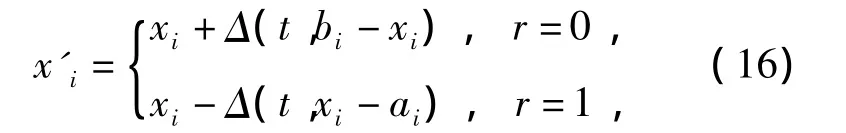
式中:xi为个体x中的一个变异点，该处基因值取值范围为［ai，bi］;r为随机数;Δ(t，y)表示［0，y］范围内符合非均匀分布的一个随机数，这里采用Δ(t，y)=yr1(1-t/T)b。其中，r1为［0，1］中的随机数;t为当前进化代数，T为最大进化代数;b为一个给定的参数，取b=3;最后，对新个体x'i实施取整操作。

(6)算法终止条件

考虑到实际作战中，要求能够在有限时间内完成雷达干扰任务分配，这里采用“指定遗传进化代数”作为算法终止条件。

4 算例分析

当干扰站数量m大于敌来袭的机载雷达数量n时，需要构造(m-n)个虚拟雷达，进行一对一的分配，得到最佳分配方案，之后将分配给虚拟雷达的干扰站重新分配给敌机载雷达;当m＜n时，首先对雷达进行整合，然后构造(n-m)个虚拟雷达，进行一对一的分配，得到最佳分配方案，此时实现了一对多分配，但实质仍然是一对一分配;当m=n时，直接进行一对一的分配。其中，规定每部干扰站对增加的虚拟雷达的干扰效益和虚拟干扰站对每部雷达的干扰效益均为0。不论是何种情况下的干扰任务分配，其基础都是一对一分配。为此，本文的算例主要针对m=n的情况。

假定我方现有10个雷达干扰站，敌来袭飞机个数为10个，现需要对敌机的机载雷达进行干扰。假定由计算得到10个雷达的威胁程度评估值(单位为1)如表1所示。

依据各干扰站和各机载雷达的位置参数和性能参数，由本文所建立的模型，可求得各干扰站对各机载雷达的干扰效果评估矩阵，如表2所示。

依据上面的敌机载雷达威胁度评估值和雷达干扰效果评估矩阵，依据本文建立的要地防空作战雷达干扰任务分配模型对雷达干扰任务分配问题进行求解。在运用遗传算法对本文的模型进行求解时，设定初始个体数为40，最大遗传代数为200，作为算法终止条件。

经过200次遗传迭代后，雷达干扰任务分配方案见表3。

表1 敌机载雷达威胁度评估值Table 1 Evaluation of airborne radar menace degree

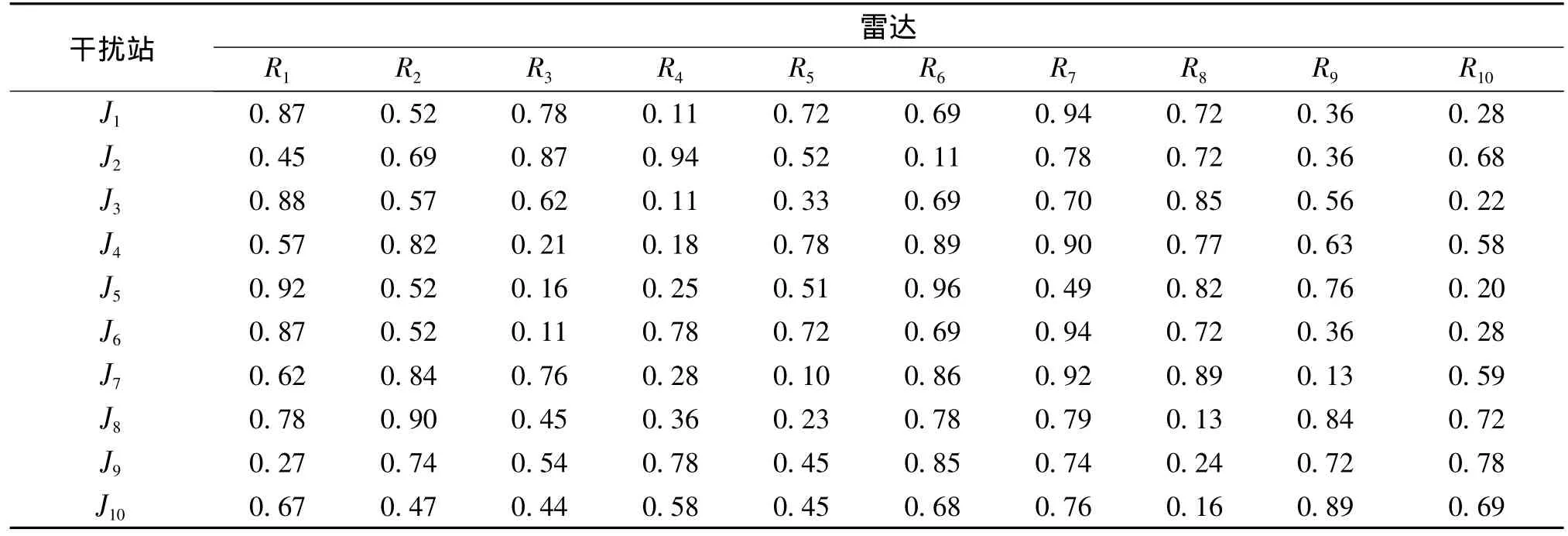
表2 雷达干扰效果评估矩阵Table 2 Evaluation matrix of radar jamming effect

表3 雷达干扰任务分配方案Table 3 Scheme of radar jamming task assignment

与此方案相对应的总干扰效益值为5.749 6。图1为经过200次迭代后优化分配方案的目标函数值及性能跟踪。

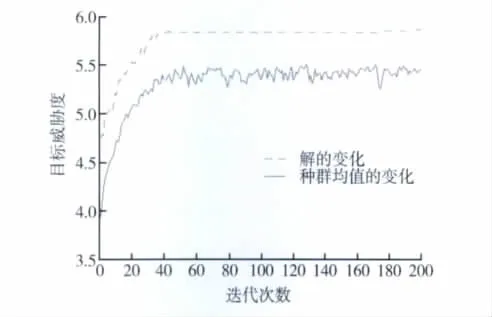
图1 经过200次迭代后优化分配方案的目标函数值及性能跟踪Fig.1 Target function and performance tracing of task assignment through 200 times iterations

从仿真算例可以看出，本文所建立的模型能够有效地解决雷达干扰任务分配方案的优化问题，能够快速得到雷达干扰任务分配的优化方案。

5 结束语

本文首先针对要地防空作战雷达干扰任务分配中干扰站与雷达数量的对比情况进行了分析处理，实现了干扰站对雷达的一对多分配。其次，选取干扰频率、功率、时机及样式4个指标对雷达干扰效果进行评估，并结合目标雷达的威胁度评估值，建立了雷达干扰任务分配模型。再次，用遗传算法求解全局最优解，得到了雷达干扰任务分配的优化方案。最后，结合来袭目标雷达的数据及我干扰站的性能等，给出了算例分析。算例表明了所建模型的有效性和优越性。

［1］ HOLLAND J H.Adaptation in Natural and Artificial Systems［M］.Ann Arbor:University of Michigan Press，1975.

［2］ MITCHELL M.An Introduction to Genetic Algorithms［M］.Cambridge，MA:MIT Press，1996.

［3］ 郭小一，袁卫卫，黄金才.雷达干扰资源一对多分配方法［J］.火力与指挥控制，2008，33(12):22-29.GUO Xiao-yi，YUAN Wei-wei，HUANG Jin-cai.Research on Method of Radar Jamming Resource Distribution basie on One-Jammer to Multi-Radar［J］.Fire Control and Command Control，2008，33(12):22-29.

［4］ 林乔木，唐少伯.地多目标模糊优选动态规划在舰艇雷达干扰资源分配中的应用［J］.系统工程与电子技术，2007，29(3):396-398.LIN Oiao-mu，TANG Shao-ho.Application of Multi-Objective Fuzzy Optimum Dynamic Programming Theory in Radar Jamming Resource Distribution of Warship［J］.Systems Engineering and Electronics，2007，29(3):396-398.

［5］ 王杰贵，罗景青.多对多雷达干扰效果模糊综合理论评估［J］.雷达与对抗，2000，20(3):11-16.WANG Jie-gui，LUO Jing-qing.Fuzzy Comprehensive Theoretical Evaluation of Multi-Jammer to Multi-Radar Jamming Effect［J］.Radar＆Ecm，2000，20(3):11-16.

［6］ 任松，司长哲，雷军.雷达干扰站分配的模糊多属性动态规划模型［J］.系统工程与电子技术，2008，30(10):1909-1913.REN Song，SI Chang-zhe，LEI Jun.Fuzzy Multi-Attribute Dynamic Programming Model for Radar＇s Disturbing Machine Allocation［J］.Systems Engineering and Electronics，2008，30(10):1909-1913.

［7］ 崔宗国.雷达对抗原理［M］.北京:国防工业出版社，1998.CUI Zong-guo.Radar Countermeasure Theory［M］.Beijing:National Defense Industry Press，1998.

［8］ 魏保华，吕晓雯，王雪松，等.雷达干扰效果模糊综合评估方法研究［J］.系统工程与电子技术，2000，22(8):68-71.WEI Bao-hua，LÜ Xiao-wen，WANG Xue-song，et al.The Method of Fuzzy Synthetic Evaluation on Radar Jamming Effects［J］.Systems Engineering and Electronics，2000，22(8):68-71.

［9］ 陈水利，李敬功，王相公.模糊集理论及其应用［M］.北京:科学出版社，2006.CHEN Shui-li，LI Jing-gong，WANG Xiang-gong.Fuzzy Theory and Application［M］.Beijing:Science Press，2006.

［10］ 刘宝碇，赵瑞清，王纲.不确定规划及应用［M］.北京:清华大学出版社，2003.LIU Bao-ding，ZHAO Rui-qing，WANG Gang.Uncertain Programming with Applications［M］.Beijing:Tsinghua University Press，2003.

［11］ 贾斌，肖兵，金宏斌.改进遗传算法在雷达网目标分配中的应用［J］.计算技术与自动化，2008，27(4):80-83.JIA Bin，XIAO Bing，JIN Hong-bin.Application of an Improved Genetic Algorithm on Radar-Netting Objectdistribution［J］.Computing Technology and Automation，2008，27(4):80-83.

［12］ 高彬，吕善伟，郭庆丰，等.遗传算法在电子战干扰规划中的应用［J］.北京航空航天大学学报，2006，32(8):933-936.GAO Bin，LÜ Shan-wei，GUO Qing-feng，et al.Genetic Algorithm Approach to the Jammer＇s Layout for EW［J］.Joumal of Beijing University of Aeronautics and Astronautics，2006，32(8):933-936.