2012年高考解析几何大题亮点之定点、定值

☉北京丰台二中 甘志国（特级教师）

2012年高考解析几何大题亮点之定点、定值

☉北京丰台二中 甘志国（特级教师）

笔者发现，在2012年高考卷中有多道解析几何大题是考查定点、定值问题的，本文将分析、推广这样的五道高考题.

高考题1（2012年湖南理21）在直角坐标系xOy中，曲线C1上的点均在C2：（x－5）2+y2=9外，且对C1上任意一点M，M到直线x=－2的距离等于该点与圆C2上点的距离的最小值.

（1）求曲线C1的方程；

（2）设P（x0，y0）（y0≠±3）为圆C2外一点，过P作圆C2的两条切线，分别与曲线C1相交于点A，B和C，D.证明：当P在直线x=－4上运动时，四点A，B，C，D的纵坐标之积为定值.

下面给出这道高考题的一般情形.

定理1 在平面直角坐标系xOy中，动点P在定直线x=h上，过点P能作定圆Ω：（x－p）2+y2=r2（r＞0）的两条不同切线（切线的斜率存在），且分别与定抛物线Γ：y2=4px（p＞0）交于点A，B和C，D（这四个点互不相同），则这四个点的纵坐标之积为定值的充要条件是p2=r2+h2，且定值为16p2h2.

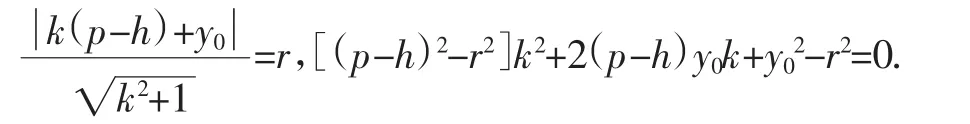
设切线PAB，PCD的斜率分别为k1，k2，得

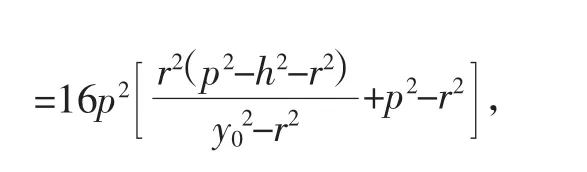
所以可得欲证结论成立.

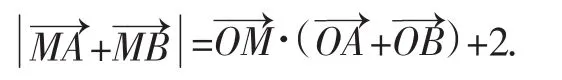
（1）求曲线C的方程；

（2）动点Q（x0，y0）（－2＜x0＜2）在曲线C上，曲线C在点Q处的切线为l.问：是否存在定点P（0，t）（t＜0），使得l与PA，PB都相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值.若不存在，说明理由.

本题第（2）问的一般情形：

定理2 设定点A，B在定抛物线Γ：x2=2py（p＞0）上且关于y轴对称，点Q是抛物线弧A（B上的任意一点（但不是端点），则存在定点P（0，t）（t＜0）使得Γ在点Q处的切线l与直线PA，PB都相交，交点分别为D，E且△PDE与△QAB的面积之比是定值λ的充要条件是t为点A的纵坐标的相反数（且定值λ=）.

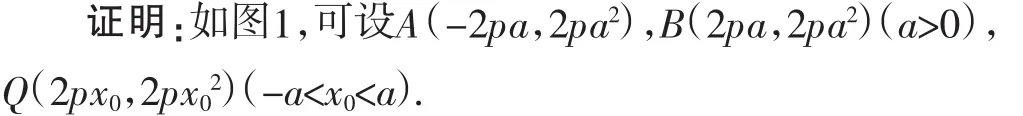
可求得切线l：y=2x0x－2px02，切线l与y轴的交点C（0，－2px02），直线

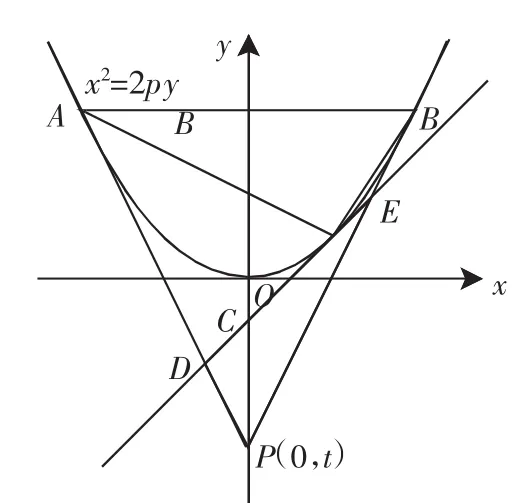
图1

即切线l与直线PA，PB都相交的充要条件是t≤－2pa2.

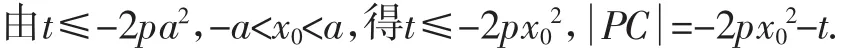
当t≤－2pa2时，可求得切线l与直线PA，PB的交点D，E的横坐标分别为

从而可得欲证结论成立.

高考题3（2012年上海理22）在平面直角坐标系xOy中，已知双曲线C1：2x2－y2=1.

（1）过C1的左顶点引C1的一条渐进线的平行线，求该直线与另一条渐近线及x轴围成的三角形的面积；

（2）设斜率为1的直线l交C1于P、Q两点，若l与圆x2+y2=1相切，求证：OP⊥OQ；

（3）设椭圆C2：4x2+y2=1，若M、N分别是C1、C2上的动点，且OM⊥ON，求证：O到直线MN的距离是定值.

本题第（3）问的一般情形是：

设点O到直线MN的距离是d，得

从而可得欲证结论.

高考题4 （2012年福建文21）如图2，等边三角形OAB的边长为8，且其三个顶点均在抛物线E：x2=2py（p＞0）上.

（1）求抛物线E的方程；

（2）设动直线l与抛物线E相切于点P，与直线y=－1相交于点Q.证明以PQ为直径的圆恒过y轴上某定点.

参考答案：（1）x2=4y；（2）以PQ为直径的圆恒过y轴上的定点（0，1）.

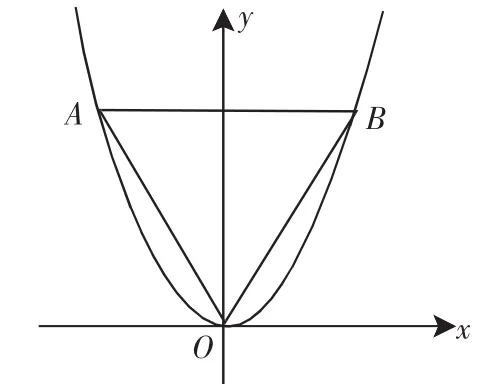
图2

（1）求椭圆E的方程.

（2）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由.

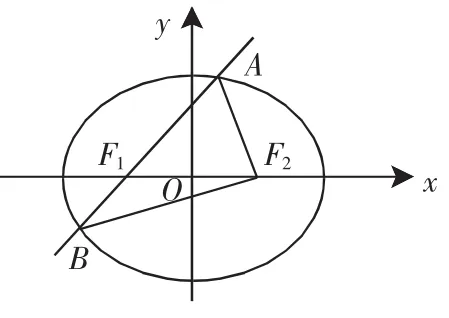
图3

上述两道高考题的一般情形：

定理5 设动直线p与圆锥曲线Γ相切于点P，与Γ的一条准线l交于点Q，则以PQ为直径的圆恒过定点，且该定点就是Γ的与准线l对应的焦点F.

证明：（1）先证抛物线的情形.

因为t∈R时该式恒成立，所以由多项式恒等定理，得

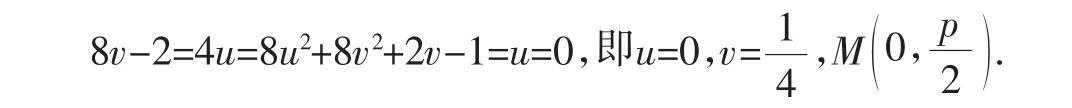
（2）再证椭圆的情形.

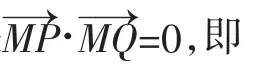
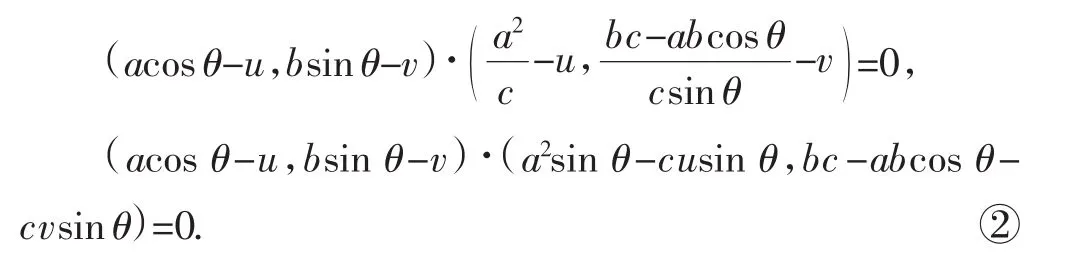
因为该式在0＜θ＜π时恒成立，所以左边在θ→0时的极限为0，得v=0，所以

所以以PQ为直径的圆恒过定点，且该定点就是Γ的与准线l对应的焦点F（c，0）.

（3）再证双曲线的情形.

还可验证当u=c，v=0时，③式恒成立.

所以以PQ为直径的圆恒过定点，且该定点就是Γ的与准线l对应的焦点F（c，0）.