函数符号f（x）中“对应关系f”特征解读

☉甘肃省天水市第一中学 宫前长

函数符号f（x）中“对应关系f”特征解读

☉甘肃省天水市第一中学 宫前长

人教A版《数学》（必修1）“函数及其表示”给出了函数的定义及其表示，但学生在学习过程中仍然感到：理解困惑多、解题疑虑多.究其原因不外乎对函数概念的理解有问题，下面从几个方面对f（x）中“f”的特征解读如下：

一、函数概念的基本特征

函数概念的学习，主要表现在对概念的抽象性、多元性、层次性和系统性等几个方面的理解和深层解读.

1.函数概念的形成过程凸现出抽象性

函数在初中就有了一种描述性的定义（变量说法），即有些变量和变量之间存在着依赖关系，一个量的变化引起另一个量的变化，这样就建立起了反映变量之间相互依赖关系的概念——函数关系，形成了简单的函数概念，未涉及函数符号f（x），虽然这样的描述并不是十分严格，但这是认识函数关系的一个重要视角，从一个方面，揭示了函数的本质.学生学习的函数是一些简单的、具体的函数，如正比例函数、反比例函数、一次函数和二次函数.

从常量到变量，这是认识函数思想的一个飞跃.函数可以简单地理解为一个变量与另一个变量之间的一座“数量桥”，函数是“数量桥”就已经表明了函数的功能：运算，即给一个具体的自变量的值，通过具体的解析式求出对应的函数值.

进入高中函数的定义由原来的“变量说”过渡到“对应说”，对函数有了更深入的诠释.函数定义的深刻涵义是通过对本质属性（对应）的挖掘、思考，经抽象之后的数量之间的对应关系，采用特定的数学符号f（x）表示.函数符号f（x）中蕴藏着函数形式化的对应关系“f”.这就说明函数概念形成的过程实质上是抽象出某一类数对应共同本质属性的过程.

2．函数概念的表征形式体现出多元性

函数概念的表征形式多样，如表格、图像、符号、解析式等.不同的表征含有不同的思维方式.从表格、图像等函数表征形式（直观、形象），到采用解析式、符号等函数表征形式（抽象），最后到抽象思考（直接采用函数符号进行思维操作），呈现出函数概念的表征形式具有多元性特征.

3．函数概念的理解深度表现出层次性

函数概念的抽象性表明学习函数时要按层次递进的过程进行，这样才能不断深入地抽象概括函数概念，更好地把握函数的本质.虽然函数概念的多元表征体现了不同的理解层次，但其本质是不变的.

对形式化的函数符号f（x）、对应法则“f”的涵义的认识基本上集中在理解“f”上，如：①对应关系“f”在变量x取什么范围内的实数时才成立；②对应关系“f”对给定的实数x作用之后的结果是f（x）；③对应关系“f”体现出具体的算法要确定、清楚.

4．函数概念的内涵把握呈现出系统性

函数概念具有很强的系统性，小学阶段数、量、图、数据（一批数）是引导儿童进入数学的源泉，数和量常常交织在一起，常说数量，数是用来刻画量的大小的一种工具.初中阶段，有两种量（常量和变量），或有些量是已知的，有一些是未知的，渗透未知量的概念，在量的认识上是个飞跃，接着建立起了反映变量之间相互依赖关系的概念——函数关系（变量说）.高中阶段利用更丰富的实例引导学生认识函数是刻画日常生活和其他学科规律的重要数学模型，由于函数模型的重要地位，进一步抽象概括出函数的严格数学定义.在直角坐标系中，函数图像就像一座桥梁把变量x和y联系起来了.

二、剖析函数定义

1.从教材编排来分析

函数的定义在初中阶段采用传统方式定义，即“设在某变化过程中有两个变量x、y，如果对于x在某一范围内的每一个确定的值，y都有唯一确定的值与它对应，那么就称y是x的函数，x叫做自变量”；在高中阶段函数的定义采用近代定义方式，即“设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数（function）.记作：y=f（x），x∈A.”

传统定义是从运动变化的观点出发，而近代定义是从集合的对应、映射的观点出发，侧重点不同，体现的涵义也不同，自然理解的层次、方式也不同.在近代定义中，x叫做自变量，x的取值范围A叫做函数的定义域（domain）；与x的值相对应的y值叫做函数值，函数值的集合{f（x）︳x∈A}叫做函数的值域（range）.函数符号“y=f（x）”中的f（x）表示与x对应的函数值，是一个数，而不是f乘x的积，进一步让学生体会函数是描述变量之间依赖关系的重要数学模型，并能用集合与对应的语言来刻画函数，感悟对应关系“f”在刻画函数概念中的作用.让学生在不同学习阶段采用不同的函数定义编排方式，逐步引导学生理解函数定义经历从简单走向深层，从而提升了学生的思维层次.

2.从数学角度来分析

由函数概念的定义可知，理解函数关键要以对应法则“f”的意义理解作为基础，进一步加深对函数符号f（x）的本质理解、把握.明确函数符号f（x）不仅要把f（x）看成一个数值（函数值），还要看成一个对应法则“f”作用变量x的一个过程，同时还要看成一个对应法则“f”作用变量x的算法，理解这一点在数学角度来看是很重要的.

如果在同一道数学题中出现f（x）和f（2x-1），就已经表明两个函数是由同一个对应法则“f”形成的，在逻辑联系上具有很强的抽象性，数学形式化符号表示使两个函数的定义域指向不同的范围.

3.从教学角度来分析

函数概念的教学中，一定要讲清函数概念形成的思路，逻辑严谨.表述准确、简捷规范，数学符号表述要完整.使函数概念形成过程的抽象性和学生的认知结构、经验“对接”顺利，为更好地将函数知识的学术形态转化为教育形态起到重要的作用.下面通过一个数学案例来剖析：

案例：已知函数f（x）的定义域是［-2，5］，求函数f（2x-1）的定义域.

剖析：前面学过函数符号f（x）是一个抽象形式化的符号，其中蕴藏着丰富的涵义，只有深刻理解，才能清楚、明白函数符号f（x）鲜活生动的本质涵义.牢牢抓住函数概念的定义，明白函数符号f（x）与f（2x-1）的数学涵义，揭开数学形式化表示的“外壳”，透过形式表示弄清f（x）与f（2x-1）的定义域的本质含义，才能让学生进一步的深层次理解函数的概念.

函数f（x）的定义域是［-2，5］是指对应关系“f”作用的对象x∈［-2，5］时才有意义，从而可以推知f（2x-1）中的对应关系“f”作用的对象2x-1∈［-2，5］时才有意义，此时x的范围就是函数f（2x-1）的定义域.

从上述的案例剖析可知，重点让学生深刻理解对应关系“f”的涵义，需要分步递进的方式，通过实际案例从不同的层面逐渐理解，对核心内容全面把握.若对“自变量的取值范围”、“对应关系”的关注不全面，则导致对函数概念（定义域、对应关系和值域）缺乏系统性认识，自然削弱了定义域对函数重要性的认识.

4.从学生角度来分析

刚上高中的学生对函数的概念理解存在的问题有：对函数定义域的理解不到位，心理仍处在初中的变量阶段，对函数符号f（x）的理解只是一种感性认识，尤其是函数形式化的符号表示不习惯、不规范、不完全明白，在处理与函数相关的问题时就会存在认识上弄不清、逻辑上理不顺的困难，解决这个问题的关键还是对函数符号f（x）中对应关系“f”的理解.

三、案例剖析

1.案例

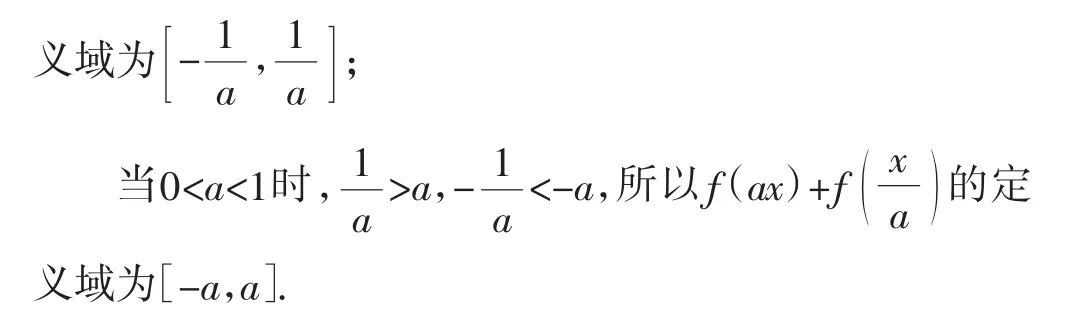
2.案例中函数f（x）中“f”表征的特征

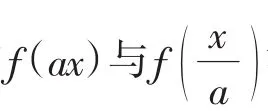
3.深层剖析

函数f（x）的定义域是自变量x的取值范围，从而深层理解为：f（x）中的x可以用任意数或代数式来替换（必须在给定范围内），但一定要牢记替换部分应与x取值范围相同.如上述案例中的整体ax或的取值范围是［－1，1］，否则会出现问题.注意：对于复合函数y=f［g（x）］的定义域依旧是指自变量x的范围，而不是中间变量g（x）范围，此时隐含了“g（x）与f（x）中的x是一致的”特征，即范围相同.函数的定义域理解了，函数的本质、灵魂就抓住了，对抽象函数问题的理解才能更深刻.解决问题时，从函数概念出发，抓住问题的本质，容易找到各问题的求解方法.可见函数概念的理解对解相关函数问题是多么的重要.

对于函数f（x）有时没有具体的解析式表示，只是数集之间一种对应关系的抽象体现，如f（f（x））表示“自变量x按照对应关系f得到的f（x）重新作为变量按照对应关系f再进行一次映射（运算）得到的函数值”.“f”的涵义在没有具体的表达式表达某种关系时，可以理解为两个数集之间“有（存在）某种”对应关系即可.

四、教学启示

1．强化函数概念的教学

函数概念的教学实质就是把抽象的函数定义与学生已有的变量描述的函数定义联系起来，实现函数概念的有效引入、理解和运用.在对函数概念的抽象化、形式化、系统化和具体化的过程中，比较、分类、类比和评价必须跟进，消除学生对数学符号形式化表示的困惑，有利于让学生对函数概念有一个完整的系统认识和理解.

2．抓牢函数主线思想

函数思想是高中数学课程的一条主线，从一个角度链接起了高中数学课程的许多内容，函数的教学一定要突出函数图像的地位.不管是用解析式法、列表法还是图像法去刻画一个具体函数时，一定要让学生在脑子里形成一个图像.只有把握住函数图像才能把握住一个函数的整体性质，这是数形结合的基础.

3．促进学生理解数学

函数概念的抽象性不能采用告知学生方式进行，一定要通过典型案例教学，牢牢抓住符号f（x）的解析式，通过剖析，深化对函数概念的定义符号f（x）的认识，寻找蕴涵其中的数学逻辑关系，让函数符号f（x）中对应关系“f”的本质显露出来，即“f”作用到x上才有意义，也突出了“f”在函数定义中的核心所在.

总之，只有深刻理解函数符号f（x）中对应关系“f”具有鲜明的对应关系、求函数值和具体操作的算法特征，深刻地强化对符号f（x）的理性思维层次的理解，才能提升学生的抽象思维能力.