对一个代数不等式的另证、加强与推广

☉上海市松江二中 卫福山

问题1：已知x，y，z是正数且x+y+z=1，求证：

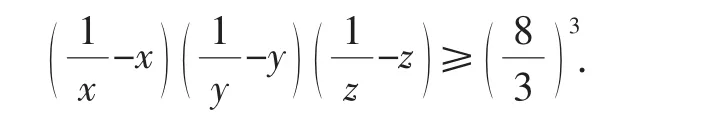
文［1］利用均值不等式给出问题1一个简单初等证明，为便于学生的理解与掌握，文［2］给出该不等式的一个加强形式：

问题2：已知x，y，z是正数且x+y+z=1，求证：

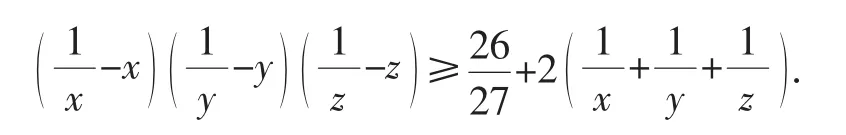
笔者阅读文［1］、［2］后受益匪浅.无独有偶，最近笔者偶然在《中等数学》杂志2006年第4期（参见文［3］）看到如下的一个问题：

问题3：已知x，y，z是正数且x+y+z=1，求证：

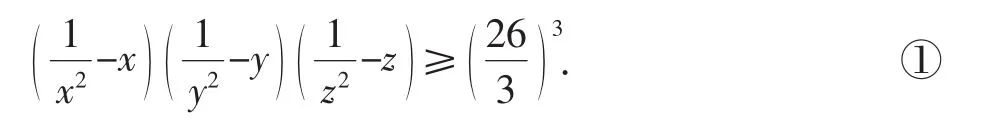
在文［3］中安振平老师也是运用均值不等式给出了证明，但技巧较大，显然问题3与问题1很相似，笔者在阅读文［1］、［2］的基础上给出问题3的另一种简单的初等证明、加强及问题1、3的一个更一般化的推广.

1.问题3的另两种简单的初等证明

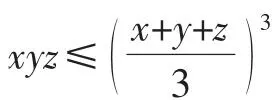
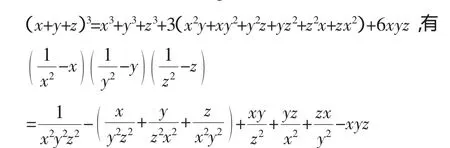
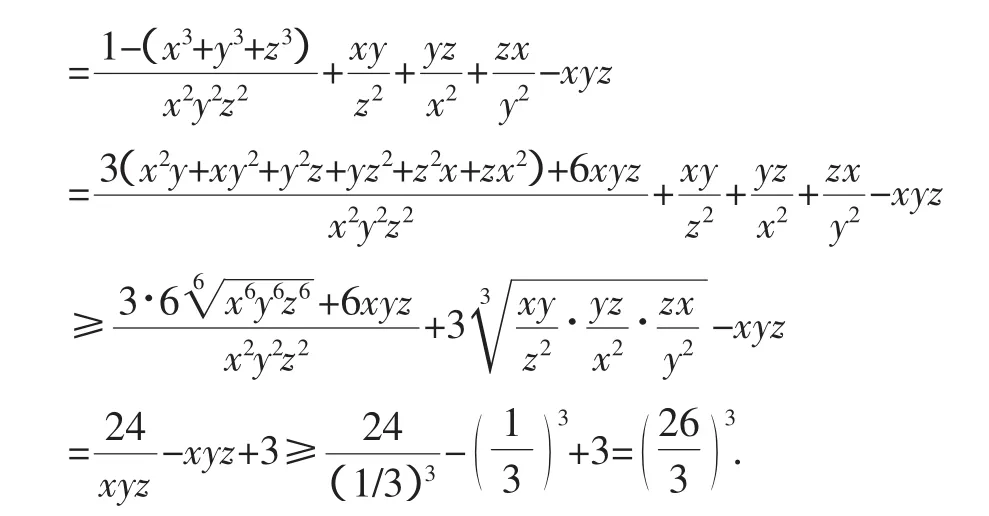
从而原不等式成立.

注：以上证明从均值不等式出发，方法与技巧简单，便于学生理解与掌握.

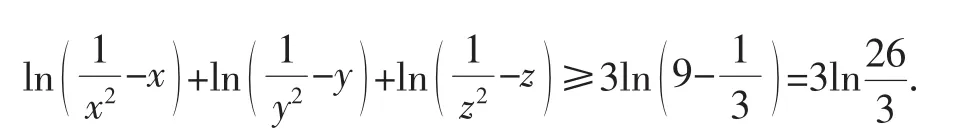
去掉对数符号即得证.

2.问题3的加强

我们可以把问题3加强如下：

问题4：已知x，y，z是正数且x+y+z=1，求证：

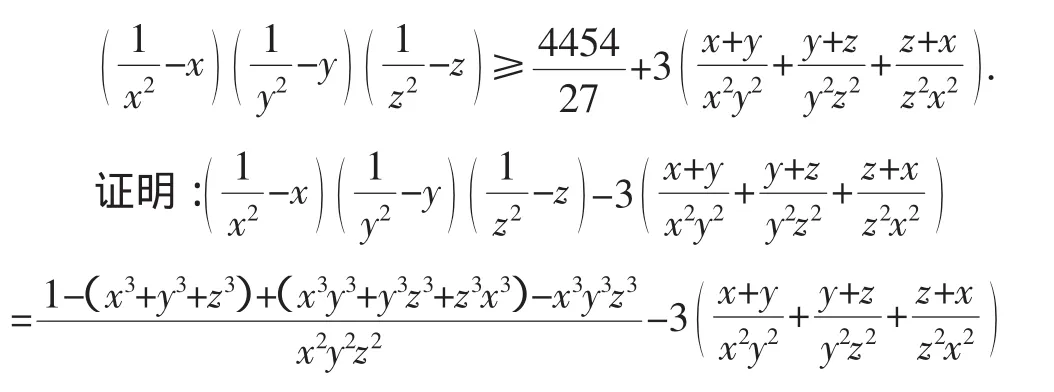
于是不等式得证.

注解：由于

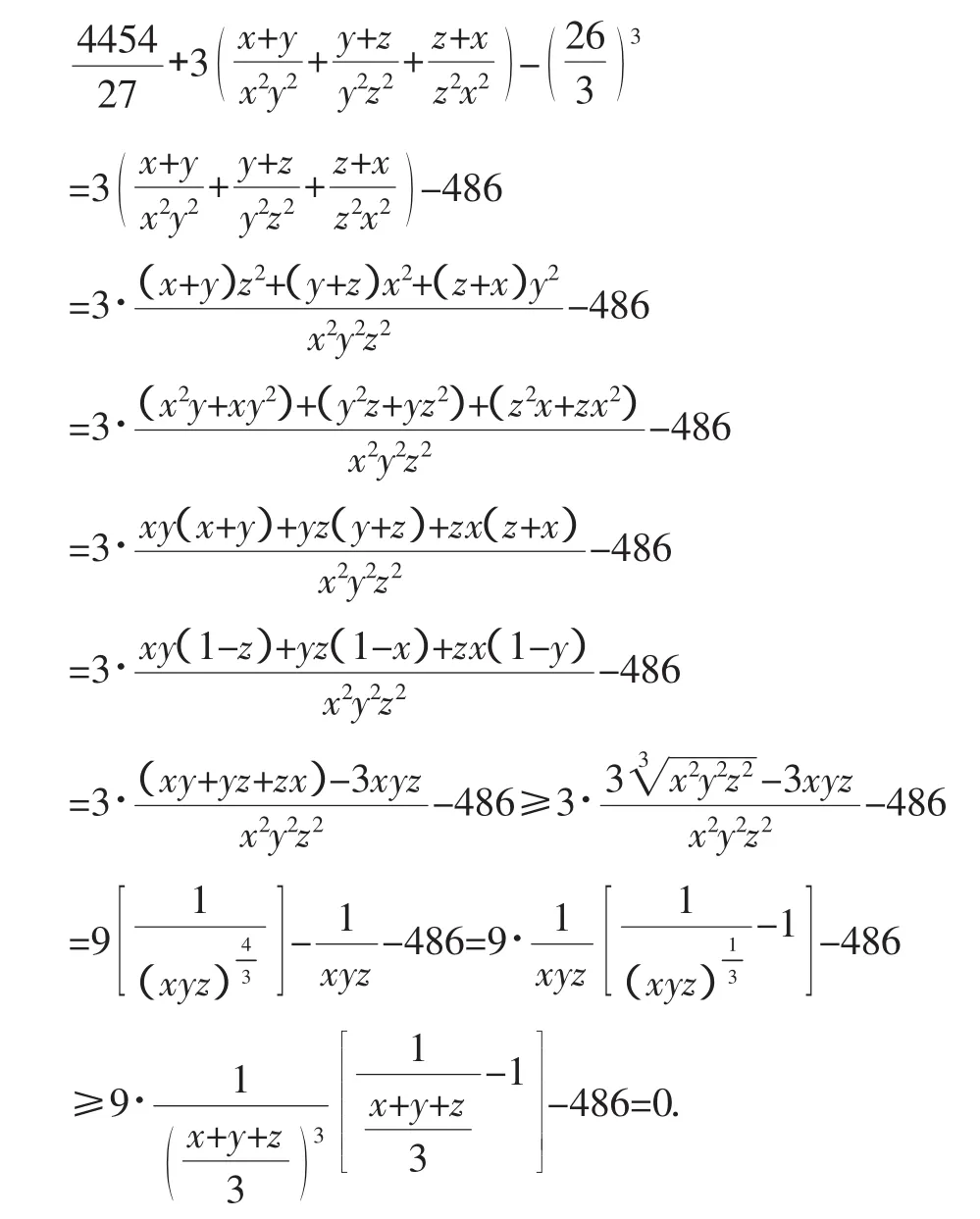
3.问题1、3的一个更一般化的推广

在以上问题1、3研究的基础上，我们可以给出更一般化的推广：

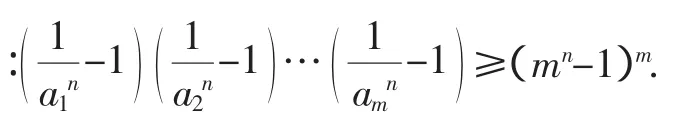
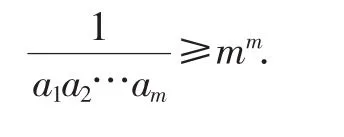
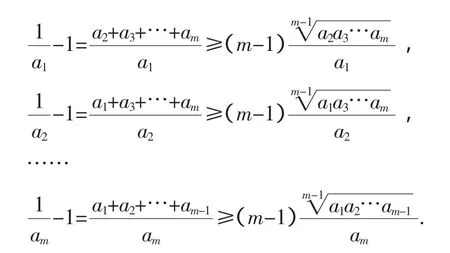
以上m个不等式相乘得

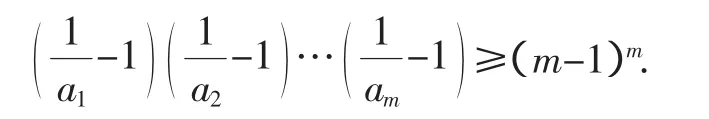
利用柯西不等式的推广有：

从而原不等式得证.

问题6：已知a1，a2，…，am∈R+且a1+a2+…+am=1，m，n，k∈N*，求证：

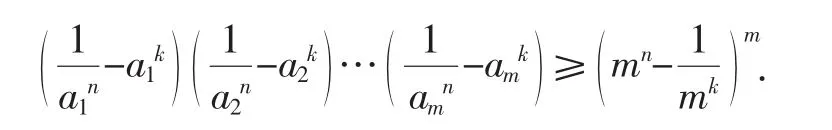
1.李歆.也谈一个不等式的简单初等证明［J］.数学通讯（下半月），2010（9）.

2.安振平.一个代数不等式的加强［J］.数学通讯（下半月），2010（9）.

3.安振平.高中问题173及解答［J］.中学数学，2006（4）.

4.蒋明斌.一个条件不等式的再推广［J］.不等式研究通讯，2006（2）. ■