经典试题 魅力绽放——对一道高考题的多种求解策略

☉江苏省丹阳市第六中学 朱万喜（特级教师）

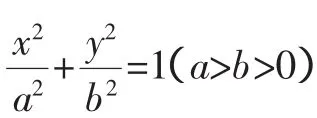
（1）求椭圆的方程；

（2）设A、B是椭圆上位于x轴上方的两点，且直线AF1与直线BF2平行，AF2与BF1交于点P.

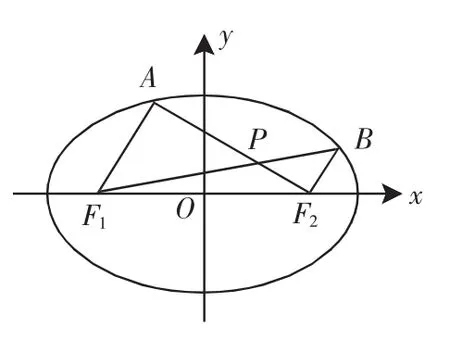
（ii）求证：PF1+PF2是定值.

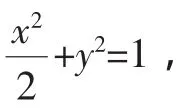
策略一：本题综合考查了椭圆的定义、标准方程及几何性质、直线方程、两点间距离公式等基础知识，第二问考查曲线与方程的关系.我们知道解析几何的本质是用代数方法研究几何问题，其核心思想是坐标法思想，联立方程组是“首当其冲”的想法.

解法1：（2）由（1）知F1（－1，0），F2（1，0），又直线AF1与BF2平行，所以可设直线AF1的方程为x+1=my，直线BF2的方程为x－1=my.设A（x1，y1），B（x2，y2），y1>0，y2>0.

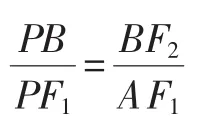
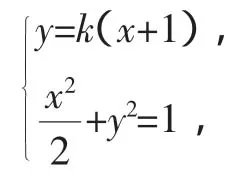
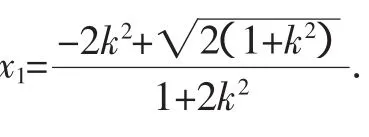
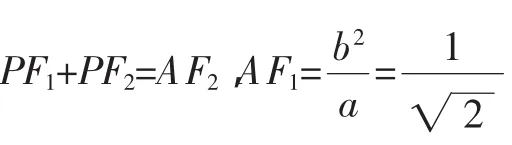
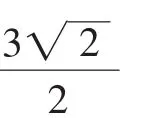
设A（x1，y1），B（x2，y2），直线AF1的方程为x+1=my，直线AF1与椭圆交于两点，一点是A，记另一点B′（－x2，－y2）.

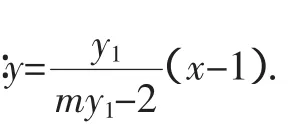
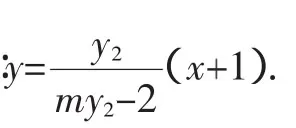
解法1是国标答案，解法2做了一些改进：其中第一小问使用焦半径公式；第二小问笔者转化为求P点轨迹问题.这两种解法虽然想法直接，但运算繁琐，过程冗长，多数学生难以“忍受”.对于解析几何问题，学生多少会有一些思路，但结果常以失败告终.根本原因是未能找到合理、便捷的将“几何问题代数化”的转化途径，导致“误入歧途”，深陷烦琐运算的“泥潭”，笔者认为对于解析几何问题还要还原“几何”本源，从题中的几何特征入手.

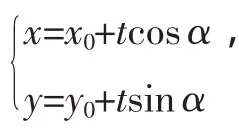
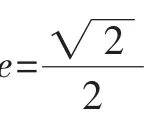
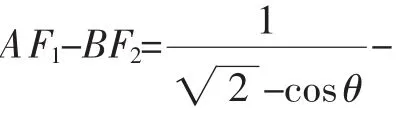
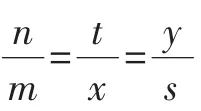
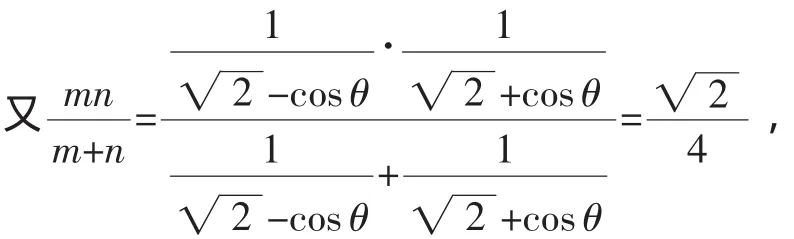
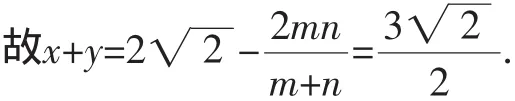
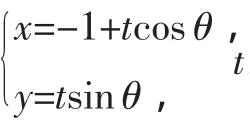
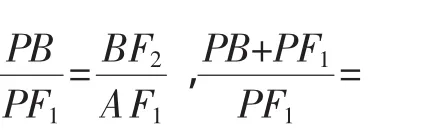
通过对解析几何的复习，让学生体验感悟数学知识之间的本质联系；拓展研究创新视野；培养综合分析问题及应用数学知识解决问题的能力，使解析几何复习更有针对性，从而提高复习的效率，这样才能在高考中立于不败之地.■