活用高考题进行解题教学的若干途径

☉湖北省武汉市黄陂区第一中学盘龙校区 李红春

活用高考题进行解题教学的若干途径

☉湖北省武汉市黄陂区第一中学盘龙校区 李红春

高考题凝结了命题专家的智慧和心血，极富代表性和示范性，对其进行深入的探索、延伸拓展、挖掘其潜在的价值，既能有效激发学生的学习和研究兴趣，提高思维的灵活性和实效性，又有利于把握高考动向，提升复习备考的有效性.笔者从近三年高考题中撷取几例，谈谈活用高考题进行解题教学的基本途径.

一、一题多解，让学生在发散中锻炼思维

进行一题多解的训练，能使学生广泛、综合的运用基础知识、提高基本技能.多途径、多角度地去分析问题，不仅可以帮助学生总结解题规律，达到对知识的融会贯通，而且可以发展其逻辑思维能力及综合思维能力.

一题多解是训练学生求异思维的一种很好的教学方法，对学生思维的流畅性和灵活性有很大帮助，但一题多解后，教师不能仅停留在“多解上”，有“放”还要有“收”，要善于引导学生从多种解法中找出共性，筛选出解决问题的最佳方案，这也是一题多解思维训练的最终目的.如本例中的3种解法虽各不相同，但都用到了正弦定理，将边之间的关系转化为角的正弦之间的关系，而这正是解三角形问题的核心方法.

二、多题一解，让学生在规律中掌握通法

进行多题一解训练，学生易于领悟解题规律，看清同类问题之间的本质特征，掌握解决一类问题的通法.

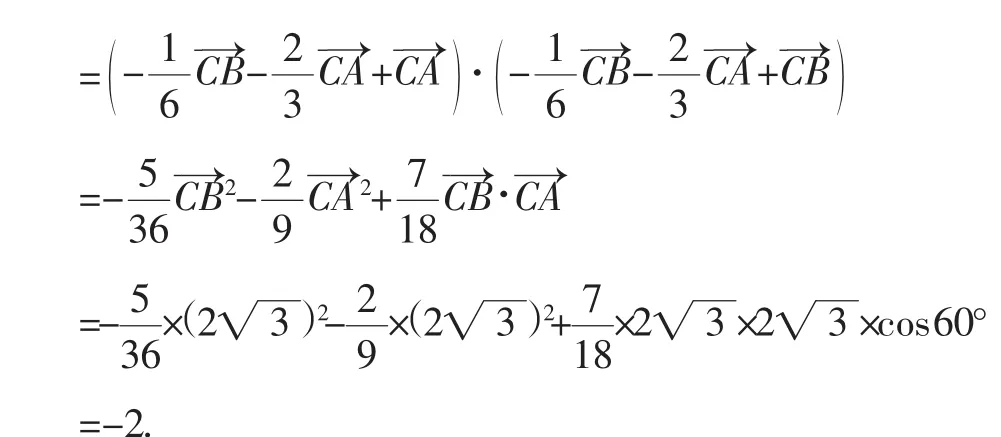
通过比较上4道高考试题的解答，求解向量数量积问题的一般方法显而易见，即合理选择两个模和夹角已知（易求）的向量作为基底，将结论中相关的向量用基底表示，再进行数量积的运算，这便是求解数量积问题的通法.

三、一题多变，让学生在拓展中提升能力

通过不断改变题设条件，使数学问题发生变化，让学生获得一题多思、一题多练的机会，可使学生的思维不断发散，能力不断提升.

以上是命题中心提供的解答.在教学中笔者发现，对于函数与导数问题，学生通常因为对分类讨论的必要性认识不足，导致思考问题不全面而出错.于是在课堂上，笔者在原题的基础上由易到难设置了三个变式，收到了很好的教学效果.

变式1：将a的范围改为0＜a＜3，其他条件不变.

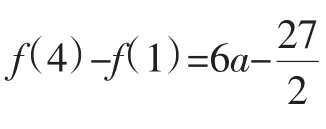
变式2：将a的范围改为0＜a＜10，其他条件不变.

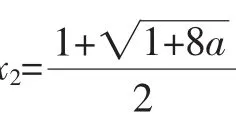
变式3：将a的范围改为－1＜a＜10，其他条件不变.

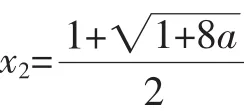
开展一题多变要努力做到变中求活、变中求新、变中求异、变中求广，避免简单的重复，变式要由易到难，层层递进，让问题处于学生思维水平的最近发展区.首先，它让学生的思维拾级而上，能力逐步提升，真正做到了复习课“低起点，高落点”的要求；其次，由于呈现的问题始终能让学生“跳一跳能摸得着”，学生能持续收获到成功的喜悦.

四、一题多问，让学生在辨析中领悟本质

这里说的“一题多问”指的是同一个问题用不同的方式呈现给学生.在解决一个问题时，首先必须要理解这个问题，即先要对它进行表征，这种表征是否准确，是否适宜，对数学问题的解决有着重大而直接的影响.有时不能解决问题，很大程度取决于问题解决者能不能正确的表征问题.

例4 （2011年重庆理10）设m、k为整数，方程mx2－kx+2=0在区间（0，1）内有两个不同的根，则m+k的最小值为（ ）.

A.－8 B.8 C.12 D.13

对于本题的条件“方程mx2－kx+2=0在区间（0，1）内有两个不同的根”，课堂教学中我给出了如下四种表征形式让学生识别，结果学生理解的情况迥然不同：

表征1：若y=mx2与y=kx－2在（0，1）上有两个不同解；

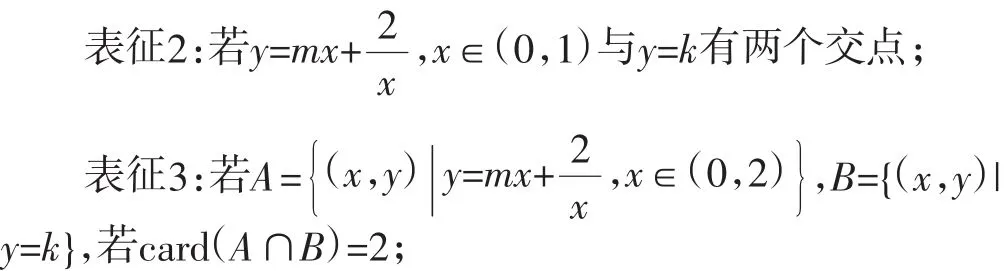
正确的语言表征是理解问题的第一步，准确的符号数式表征是解决问题的关键，表征的灵活调节有助于培养解题思维的深刻性.在数学教学中，通过设计题组进行变式训练，让学生在解决实际问题中辨析问题的实质是很有必要的.进行一题多问的变式教学，教师要有意识的引导学生从变化的现象中发现不变的本质，从不变的本质中探究变的规律.变换问题的形式，但不改变问题的本质，使学生在学习时不只是停留在事物的表象，自觉的从本质看问题，这样可以克服思维僵化和思维惰性.

教育家奥加涅相说过“必须重视很多习题潜在着进一步扩展其教学功能、发展功能和教育功能的可能性”.从以上四例不难发现，认真钻研高考试题，拓展其教育教学功能，既是高考复习的有效途径之一，更是重质轻负，摆脱题海的重要渠道.

1.毛良忠.探究多元表征途径合理解决问题［J］.中学数学教学参考（上旬），2012（1－2）.

2.吴锷.循本索源变中出彩［J］.中学数学月刊，2012（4）.