“正”“误”例说类比思想的运用
2013-08-28浙江省绍兴鲁迅中学蒋钰香
☉浙江省绍兴鲁迅中学 蒋钰香
“正”“误”例说类比思想的运用
☉浙江省绍兴鲁迅中学 蒋钰香
*该文为绍兴市“揭示错误本质,提升资源价值”——高中数学习题教学中有效利用错误资源的实践与研究的阶段性研究成果.
类比是根据两个(或两类)对象之间具有(不具有)某些相同或相似的性质,而且其中一个(或一类)还具有(或不具有)另一性质,由此推出另一个(或另一类)对象也具有(或不具有)这一性质,类比法是研究数学问题的重要方法,也是掌握知识的好方法,正如玻利亚所言:“类比是一个伟大的引路人”.在学习中正确的类比可起到事半功倍之效,但错误的类比也常为我们带来困惑.
一、“正确”的类比
1.在类比中发现和谐,简化记忆
数学,是中学课程中的一门主科,课时最多,内容浩瀚,记忆和掌握起来,都比较困难.站在系统的高度,注意知识间的类比,不但有利于抓住问题本质,而且可以找出规律即共性,简化记忆,便于掌握.数学中类比比比皆是,如指数函数与对数函数的类比、等差数列与等比数列的类比.
案例1:如在学习正比例函数y=kx(k≠0)的图像时,注意到函数的图像是随函数解析中常数k的变化而变,换言之,k决定着直线的位置,在这里,k的符号,决定着直线所在象限的位置;则决定着直线向上的方向和y轴正向夹角的大小.而当k值取遍(-∞,+∞)内的全体实数时,直线y=kx则绕原点旋转而扫遍除y轴以外的整个坐标平面(若允许k=0).在学习二次函数y=ax(2a≠0)时,可以类比y=kx(k≠0),猜想是否常数a的取值将决定曲线y=ax2的位置?结果发现a的符号决定着曲线所在的象限;则决定着曲线与y轴的相对位置;当a值取遍(-∞,+∞)内全体实数时,曲线y=ax2将扫过除y轴以外的整个坐标平面.这样在入门伊始,就抓住了学习二次函数的关键,使得利用二次函数求最大(小)值,以及解一元二次不等式等一系列问题,不难得到解决.当然,由于y=ax2的图像是一条曲线,在决定曲线与y轴相对位置的时候,已经影响了曲线的形状.另外对于幂函数、指数函数、对数函数、三角函数也可类比上面的方法研究.上述讨论,从对函数解析式中常数作用的类比分析,使我们对函数性质的认识系统化了.
2.在类比中获得命题的推广和延伸
类比思想是我们探索规律的重要途径.数学家利用类比法获得很多研究成果.在高中数学探究性学习课堂教学中,可利用类比法来研究问题.
案例2:师:你能类比圆的直径所对的圆周角是直角,因而圆上动点与直径两端点连线的斜率积为定值,kPA·kPB=-1,猜测椭圆、双曲线上动点与长轴或实轴两端点的连线斜率积为定值吗?若是,定值为多少?
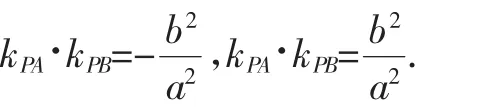
3.运用类比法编制习题
用类比法编制习题,其模式是:
原题有条件a,b,c,结论d;
新题有条件a,b,c′,结论d′.
这里的新题的条件c′和结论d′与原题的条件c和d有着对应的相似性,特殊情形下可能有d=d′,由于类比法得到的结论具有或然性,因此所得的新题的科学性必须经过严格的推敲.
案例3:平面上两条直线同垂直于第三条直线,则这两条直线平行.
将“平面上”的问题与“空间”的问题进行类比,或将其中的“两条直线”与“平面”类比,可得四个命题如下:
(1)空间两条直线垂直于第三条直线,则这两条直线平行.(假命题)
(2)空间两个平面同垂直于一条直线,则这两个平面平行.(真命题)
(3)空间两条直线同垂直于一个平面,则这两条直线平行.(真命题)
(4)空间两个平面同垂直于三个平面,则这两个平面平行.(假命题)
4.运用类比法进行新知识的探究
学生的数学学习活动不只限于接受、记忆、模仿和练习,高中数学课程还倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.这些方式有助于发挥学生学习的主动性,使学生的学习过程成为在教师引导下“再创造”的过程.在教学中应引导学生进行新知识的探究,引导学生从问题出发,通过观察,运用归纳、类比的方法首先得出猜想,然后再进行证明,这十分有利于学生对证明的全面理解.在教学过程中,为了培养学生数学创新意识,教师也要有意识地渗透类比思想方法.
案例4:“不等式基本性质”的教学,我们可以这样提出问题:
不等式的基本性质可以类比等式的性质探究过程而得到启发:
(1)等式有哪些基本性质?
(2)从等式的性质的表述中,你能发现这些性质是怎样提出的?(研究等式基本性质的思想方法是什么?)——考察等式在运算过程中的不变性;
(3)类比等式基本性质的提出过程,你能提出哪些关于不等式基本性质的猜想?这些猜想正确吗?
二、“错误”的类比
类比推理是一种或然推理,其结论是否正确有待实践来证明
1.“错误”的运算法则的类比
案例5:设a,b为非零向量,且(a+3b)⊥(7a-5b),(a-4b)⊥(7a-2b),求a与b的夹角θ.
错解:由已知(a+3b)·(7a-5b)=0,得
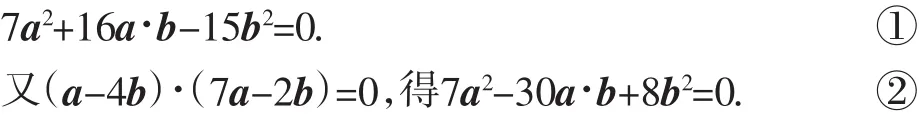
①-②得:2a·b=b2,即2a=b,所以a与b的夹角θ=0°.
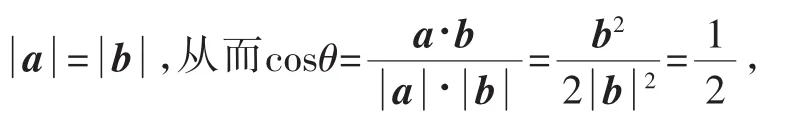
2.“错误”的数学思想类比
数学思想是对数学规律的理性认识,是数学的灵魂,我们要注重数学思想方法的学习,并在运用数学思想方法解题时谨防类比负迁移.
案例6:若数列{n2-kn}共有2012项,且单调递增,则k的取值范围是________.

剖析:数列是特殊的函数,极易选取“类比源”,并将数列的恒成立问题(目标函数)类比迁移为相应辅助函数的恒成立问题(源问题),似乎天衣无缝,可惜错了.
3.“错误”的解题方法的类比
对于教材中非通性解法或高考题中“歪打正着”的解法,教师应让学生认识到不可随意类比.

错解:依照上面例题的解法得单调递减区间不存在(具体过程这里略去).

两者仅一字之差,自然想到方法上的类比,但教材上的解法不具有通性解法,因为它要求一个周期上的整个单调递增(递减)区间在给定区间(否则就求不出单调递增(减)区间),而具体情况未必都如此.
从以上案例可以看出:类比作为一种推理方法,它既可以成就伟大的发现,也会导致“美丽”的错误,因此我们要“扬长避短”,在数学过程中为了培养学生创新意识,教师要有意识渗透类比思想方法,但也应该谨防类比惹的“祸”.
1.孙维刚.孙维刚导学高中数学.北京:教育科学出版社,1999.
2.徐斌艳.数学课程与教学论.杭州:浙江教育出版社,2003.
3.章建跃.对高中数学新课标教学的若干建议[J].中学数学教学参考,2007,3.
