含参不等式求解两视角

☉重庆市丰都第二中学校 蒋良平（特级教师）

在给高三学生的练习中有如下一道求解含参不等式问题：

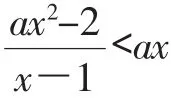
参考答案摘录如下：

①a=0时，A=（1，+∞）；

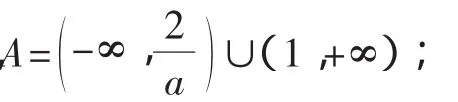
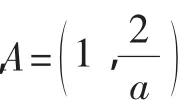
④a=2时，A=Ø；

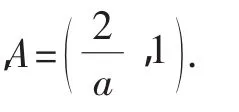
又A⊆（－∞，1），实数a的取值范围是［2，+∞）.

参考答案的解题思路是先求出集合A，然后根据A⊆（－∞，1）求出a的取值范围.

课后有学生拿出自己的一种解答询问我错在哪里?她的解答如下：

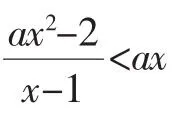
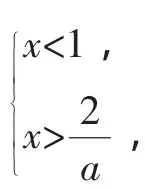
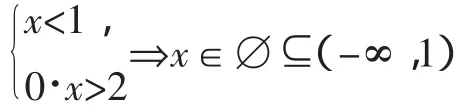
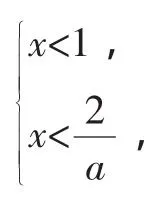
综上，满足条件的实数a的取值范围是a≥2或a≤0.

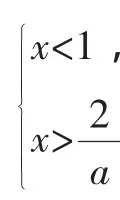
顺着该生的思路，下面给出此题的另一种解答：

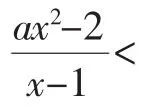
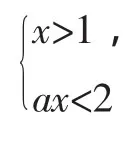
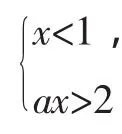
综上，满足条件的实数a的取值范围是a≥2（以上两种分类讨论的结果的交集）.

仔细比较此解与参考解答，满足条件的集合A是吻合的.而且从不等式性质角度去解释两种解答的联系很清楚，这是因为

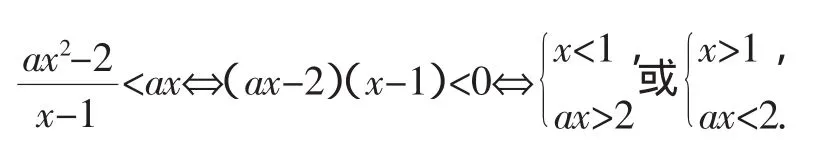
以上两种解答代表了解决含参的不等式问题的两种常用的讨论方法，即按参量与变量讨论，抓住问题的本质才能使我们高屋建瓴地看待此类含参不等式的问题.■