从不同视角探求一道课本习题中“视角”的最值问题

●韩庆文 (滕州市第一中学 山东滕州 277500)

普通高中课程标准实验教科书(人教A版)《数学》必修5习题3.4中的B组第2题如下：

题目如图1，树顶 A离地面a m，树上另一点 B离地面b m，在离地面c m的C处看此树，离此树多远时看A，B的视角最大?

分析由于在C处看A，B的视角为∠ACB，对于这一问题我们既可以从几何的角度审视，也可以从代数的角度审视.

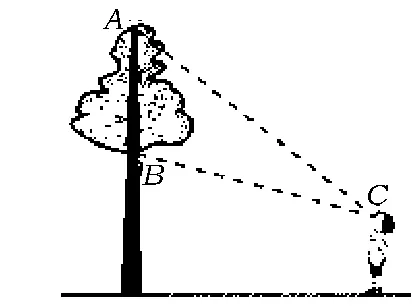
图1

从平面几何的角度考虑，可以借助于圆的有关性质.

视角1 如图2，过点C垂直于AB的直线记为DE(D为垂足).当DE与过点A，B的圆相切时，切点记为C，此时∠ACB=∠α最大.

事实上，观察图2，易得无论点C是前行还是后退到点C'，过点A，B，C'的圆必与直线DE相交，此时∠AC'B必小于圆内的∠α.当DE与过点A，B，C的圆相切且切点为C时，由切割线定理得

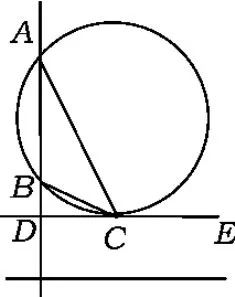
图2

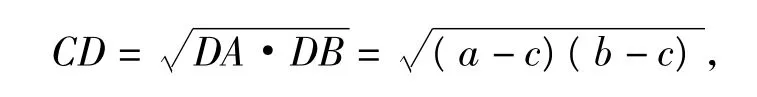
视角2 (借助于两角差的正切公式求tan∠ACB的最大值)

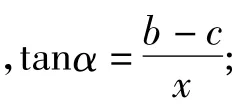
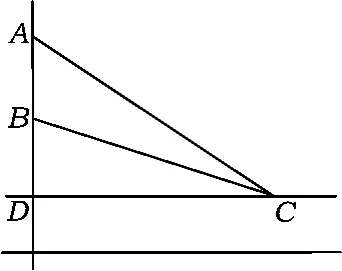
图3

视角3 (借助于正弦定理求sin∠ACB的最大值)

由视角2可得

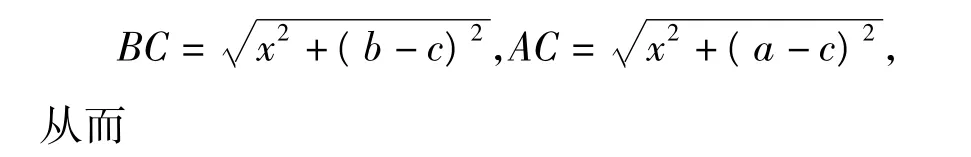
视角4 (借助于余弦定理求cos∠ACB的最小值)

由视角2可得

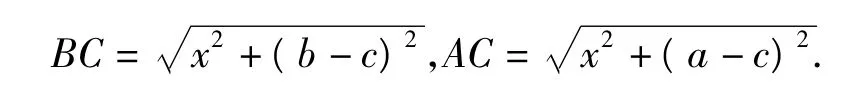
又AB=a-b，在△ABC中，由余弦定理得