3个 二 次 由 “暗” 转 “明”

●王苏文 (浬浦中学 浙江诸暨 311824)

所谓3个二次指的是二次方程ax2+bx+c=0(a≠0)、二次函数 f(x)=ax2+bx+c(a≠0)、二次不等式ax2+bx+c＞0(或＜0)(a≠0)对应于考查二次方程根的分布问题、二次函数性质(单调性、最值等)、二次不等式解或恒成立问题.对于高考而言，3个二次的考查并不陌生，几乎年年考、年年新，浙江卷很少直接考二次函数，纵观全国各个省份的高考卷，也有个别省份直接考二次函数，甚至出现考查二次函数的解答题，如湖南卷等.

仔细比较深化课程改革后的高考内容与原来新课程改革的高考内容，就会清晰地看到导数内容将不再作为高考的必修模块内容(可参考表1).如此一来，作为高中数学的重要组成部分——函数，其考查的内容可能又将回归到基本函数(指数、对数、三角函数)、常规函数(一次、二次函数)上来，毫无疑问二次函数的考查又将成为重点.

表1 深化课改前后理科部分的考试考点变化

续表1

因此，实行深化课改后对于3个二次问题应更加重视，对3个二次的问题要切实理解与掌握，否则可能在考试中吃亏.导数在列入高考内容之前的几年中，大多以二次函数为命题依据，尤其是1996年、1997年的几个二次函数问题使大多数考生都无从下手.虽然近几年对函数与导数的考查，表面上没有二次函数，但实际考查的本质还是以二次函数为主，有些高考题甚至就直接考二次函数(湖南卷、江苏卷)，二次函数问题在高考中可谓生生不息.

笔者也大致浏览了近几年的高考试卷，不难发现，高考对于二次函数的考查，有的直接考、有的间接考，以小题较多，相对而言纯粹考二次函数解答题的较少.下面通过近3年的几个有关二次函数的高考题与同行一起来了解一下高考中的二次函数问题考查.

1 直接考二次函数问题

1.1 二次方程问题

例1 设n∈N+，一元二次方程x2-4x+n=0有整数根的充要条件是n = ______.

(2011年陕西省数学高考理科试题)

分析要存在整数根，加上各个系数均为整数，故判别式必须为完全平方数才可能成立.可直接利用求根公式进行计算，然后用完全平方数与整除等进行判断计算.

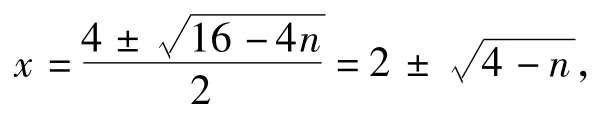
1.2 二次函数问题

例2 已知函数f(x)=x2+ax+b(a，b∈R)的值域为［0，+∞).若关于x的不等式f(x)＜c的解集为(m，m+6)，则实数c 的值为______.

(2012年江苏省数学高考试题)

分析考查二次函数的值域与二次不等式的解集问题.

解由函数的值域为［0，+∞)，得

1.3 二次不等式恒成立问题

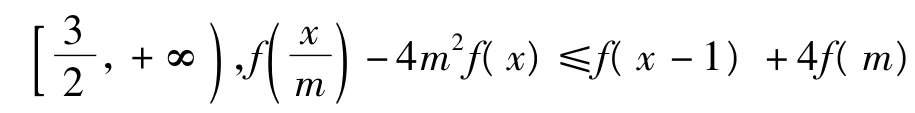
(2011年天津市数学高考理科试题)

分析本题为二次不等式恒成立问题，可先转化为二次函数问题或恒成立问题，然后用常见方法进行处理.

方法1 转化为二次函数问题处理

解不等式可化为

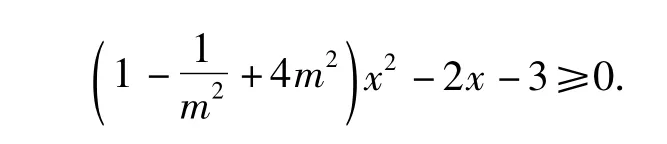
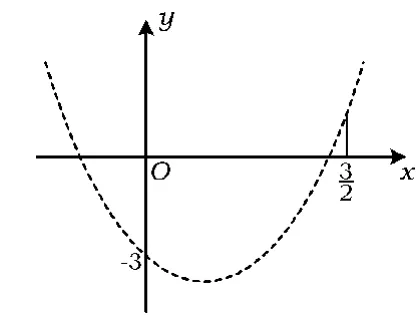
图1

因此实数m的取值范围是

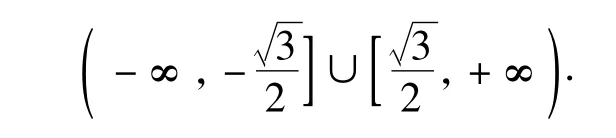
方法2 转化为恒成立问题处理

解不等式可化为

解得实数m的取值范围是

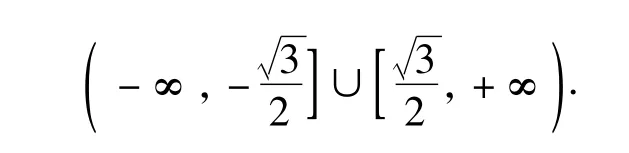
2 间接考二次问题

2.1以二次为载体，实质考查非二次

例4 设f(x)是定义R在上的奇函数，当x≤0 时，f(x)=2x2-x，则 f(1)= ( )

A.-3 B.-1 C.1 D.3

(2011年安徽省数学高考理科试题)

本题主要以二次函数为载体，考查函数的奇偶性，函数值的求法，易解.选A.

2.2 以导数为载体，实质考查二次

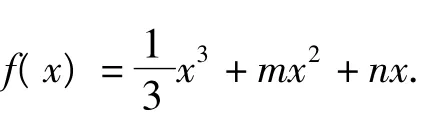
(1)如果g(x)=f'(x)-2x-3在x=-2处取得最小值为-5，求f(x)的解析式;

(2)如果 m+n＜10(m，n∈N+)，f(x)的单调递减区间的长度是正整数，试求m和n的值(注：区间(a，b)的长度为b-a).

(2011年江西省数学高考文科试题)

分析(1)略;

(2)本题的关键是二次方程f'(x)=0的2个实数根的差为整数，但不等价于2个根为整数，故求解中不能混淆.

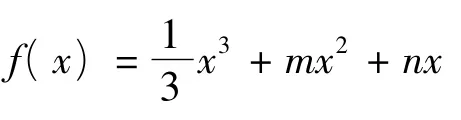
又递减区间长度是正整数，故设 f'(x)=x2+2mx+n=0的2个实数根为a，b(b＞a)，结合韦达定理

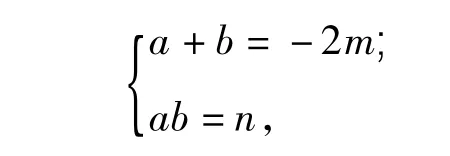
从而区间长度为b-a.又

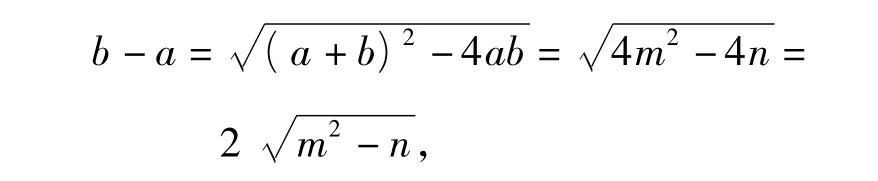
其中 m，n∈N+，m+n ＜10，且 b-a为整数，因此

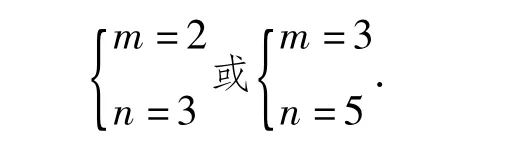
点评求解此类问题的关键是抓住不等式与方程根的思想，满足整数所需条件该如何进行转化，结合平时所学整数间的有关方法进行解答.

纵观这几年的高考试题，二次函数考查以方程、不等式为主，3个二次往往渗透于其他知识中，体现背景公平，淡中见隽.猜想在深化课改后3个二次函数的考查上会更灵活，更有深度.