二阶递推数列命题构造初探

●曹鸿德 沈新权 (嘉兴市第一中学 浙江嘉兴 314050)

本文通过对2个非线性递推数列问题的求解，探讨非线性递推数列与二阶线性递推数列之间的关系，探究一些二阶递推数列的命题是如何构造而成的，并由此讨论如何通过构造二阶线性递推数列来解决递推数列问题，希望能够给读者带来一些启发.文中的命题都选自高中数学竞赛和高校自主招生考试试题.笔者假定本文的读者已经掌握了如下的基本知识：

定义 二阶线性递推数列{an}满足：初始项a1，a2为已知，且

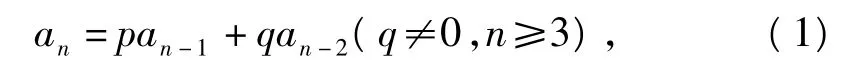
则称方程x2=px+q为数列{an}的特征方程，方程的2个根称为特征根(特征根可以是共轭无理根，也可以是共轭虚根);称数列{an}是由特征方程导出的二阶线性递推数列.

定理设二阶线性递推数列(1)的特征方程x2=px+q的2个特征根为 x1，x2，

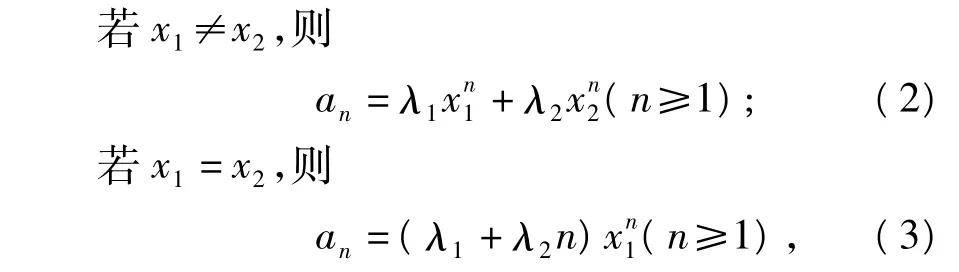
其中待定系数 λ1，λ2由初始项 a1，a2确定.

1 分式非线性递推数列与二阶线性递推数列间的相互转换

例1 设数列{an}满足：a1=a2=1，且

试问数列{an}是否是整数列?若是，请给出证明;若不是，试说明理由.

证法1 先来看参考书上的一般解法.

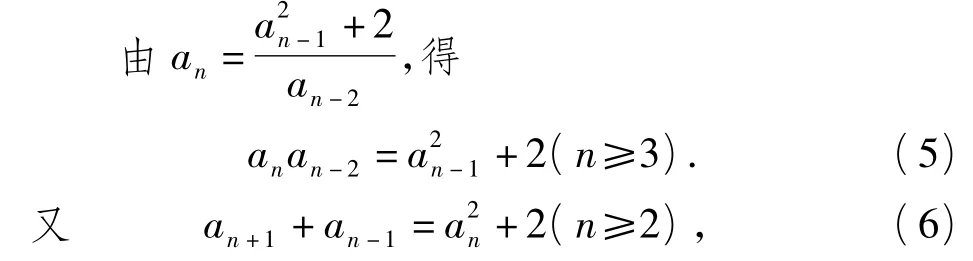
式(6)-式(5)(目的是消去常数2)，整理得

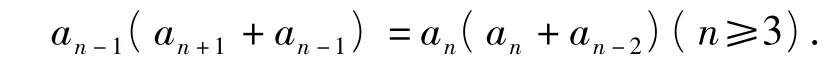
由式(1)可知an≠0(n∈N*)，故上式可化为

用数学归纳法容易证明数列{an}是整数列(略).

注证法1较为简洁，但这样的证法是如何得到的呢?为此笔者作了如下探索.

证法2 式(4)是二阶非线性递推数列，由证法1可猜想它等价于一个二阶线性递推数列(非线性的可以转化为线性的).由a1=a2=1以及式(4)，得

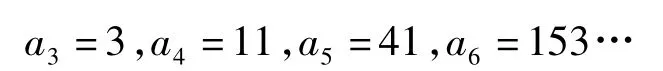
根据二阶线性递推数列的定义，设

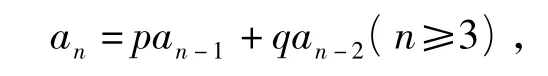
用 a3=3，a4=11 代入，得

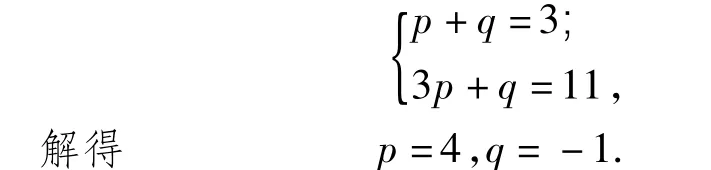
用a5=41，a6=153代入适合.于是猜想，当n≥3时，

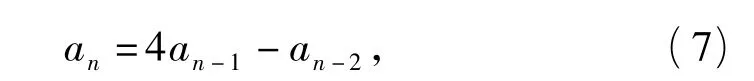
恒成立.下面用数学归纳法证明.

归纳法的奠基成立.假设当n≤k(k≥3)时，式(7)成立，则当n=k+1时，由归纳假设以及式(4)，得

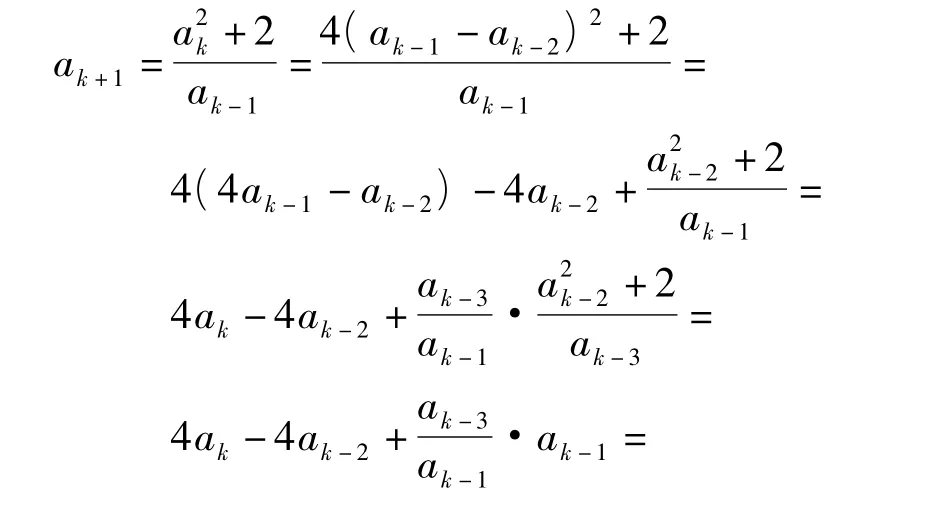
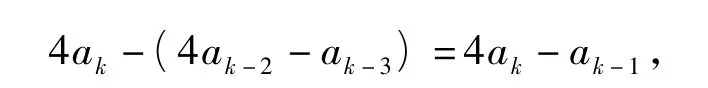
即当n=k+1时式(7)仍成立，故对一切n≥3的自然数n，式(7)恒成立.

因为a1=a2=1，所以由式(7)可用数学归纳法再证明数列{an}是整数列，并且可进一步证明数列{an}是正奇数列：这是因为a1=a2=1为奇数，an≡ -an-2(mod2).

注证法2同样完成了对例1的证明，接下来笔者关心的是例1是如何构造出来的?能否从a1=a2=1，an=4an-1-an-2(n≥3)构造出例1?

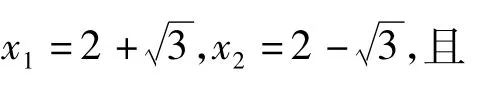
把λ1，λ2的值代入就得到数列{an}的通项公式.

由假设可知anan-2和a2n-1的展开式都是关于x1，x2的齐2(n-1)次表达式，它们之间有某种联系吗?事实上，

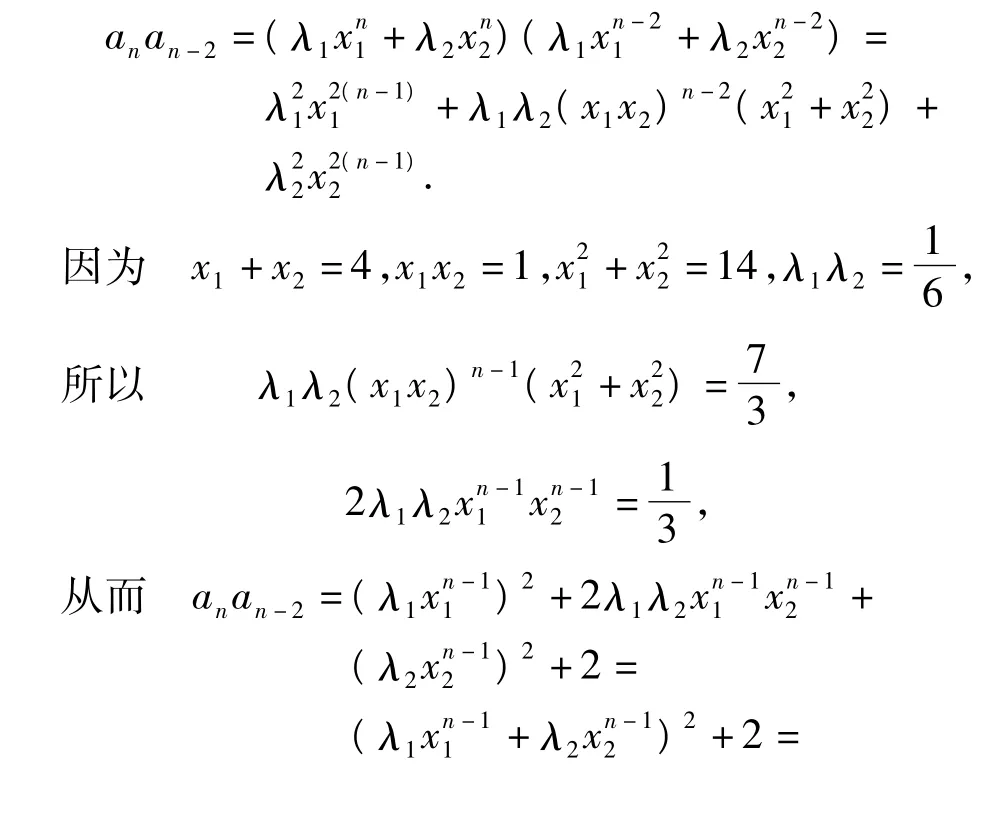
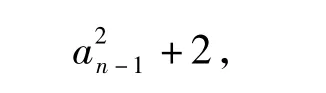
两边除以an-2，得

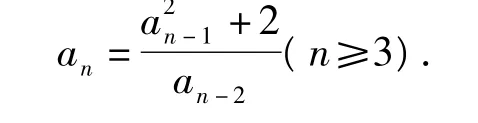
这样，就构造了例1.这一构造过程揭示了二阶线性递推数列与它的特征方程、特征根之间的关系.综上所述，得到以下等价命题：

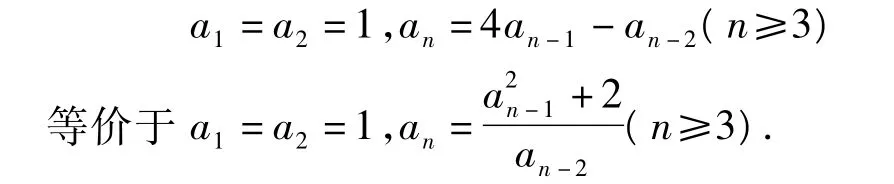
即例1是数列(7)的逆命题，例1把背景抽掉后很隐蔽，也给解题带来一定的难度.

2 数列不等式与二阶线性递推数列之间的相互转换

例2 数列{an}满足：a1=2，a2=7，且

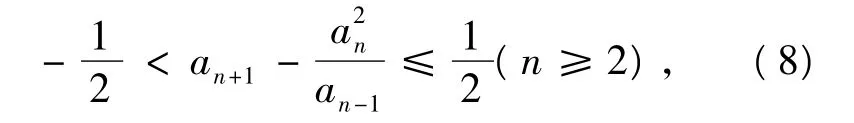
求证：当n≥2时，an是奇数.

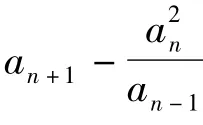
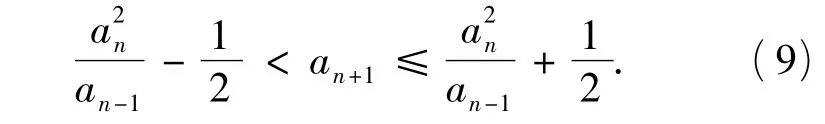
把a1=2，a2=7代入，依次得到

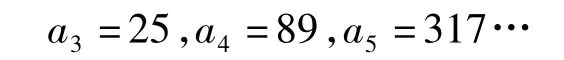
根据二阶线性递推数列的定义，设

把 a3=25，a4=89 代入，得

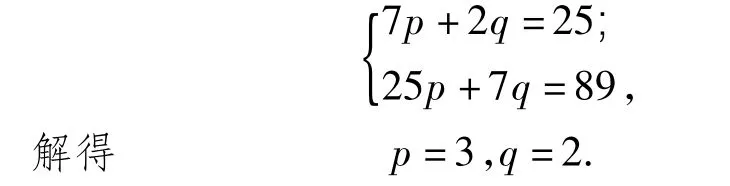
又a5=317代入是适合的.于是猜想：对于数列{an}满足

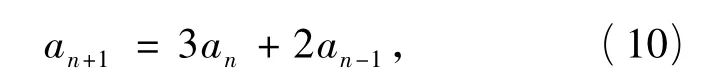
对一切n≥2的自然数n成立.下面用数学归纳法证明.

归纳法的奠基成立，且a2＞2a1.假设当n≤k(k≥2)时，ak+1=3ak+2ak-1以及 ak＞2ak-1＞0 成立，则当n=k+1时，由已知

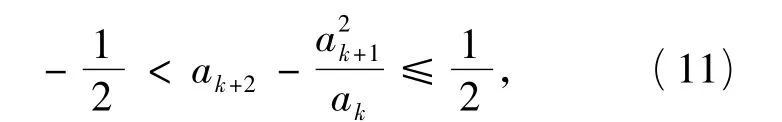
若能证明

即当n=k+1时，ak+2=3ak+1+2ak成立，故对一切n≥2的自然数 n，an+1=3an+2an-1成立.

接下来要证明式(12)成立.由归纳假设，得

成立.即当 n=k+1时，ak+2=3ak+1+2ak以及ak+1＞2ak＞0成立，故对一切 n≥2的自然数 n，an+1=3an+2an-1成立.因为 an+1≡an≡1(mod2)(n≥2)，所以从第2项起，an都是奇数.

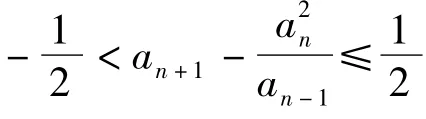
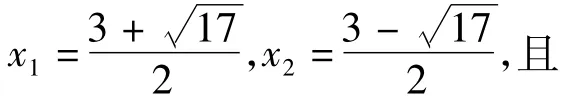
把λ1，λ2的值代入，可得到数列{an}的通项公式.

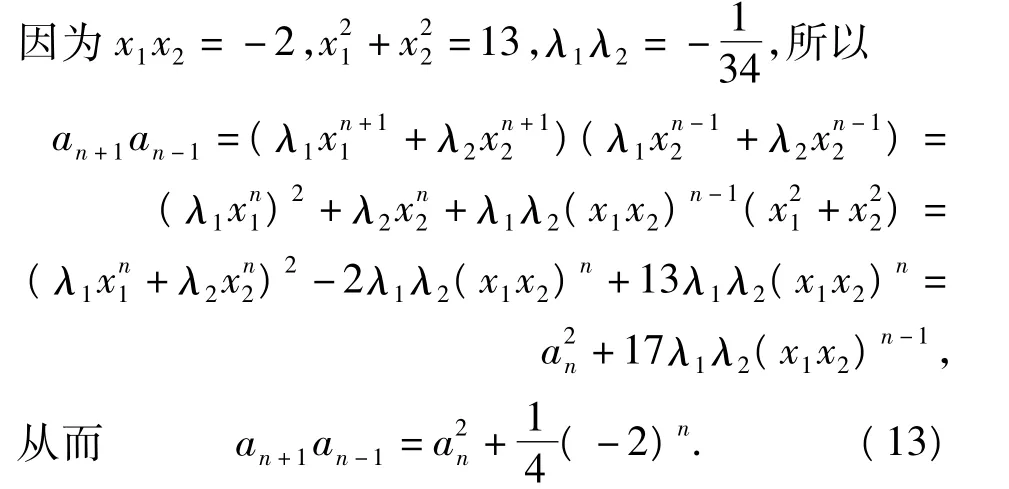
用数学归纳法可证明

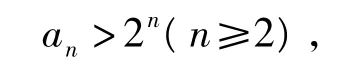
因此式(13)可化为

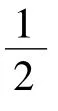
3 构造二阶线性递推数列解题

例1和例2命题构造的经验给解决以下2个问题(例3、例4)提供了策略上的帮助和指导.例3 设数列{an}满足：a1=1，a2=-1，

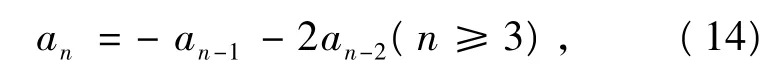
证法1 首先考虑例3的构造过程：数列(14)的特征方程为

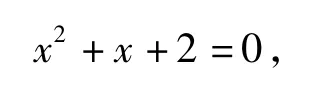
2个特征根为

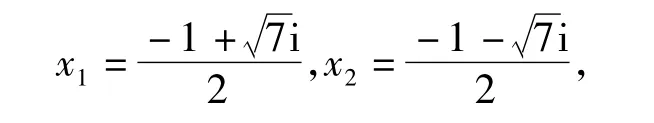
其中i为虚数单位，且

把λ1，λ2代入得到数列{an}的通项公式.因为

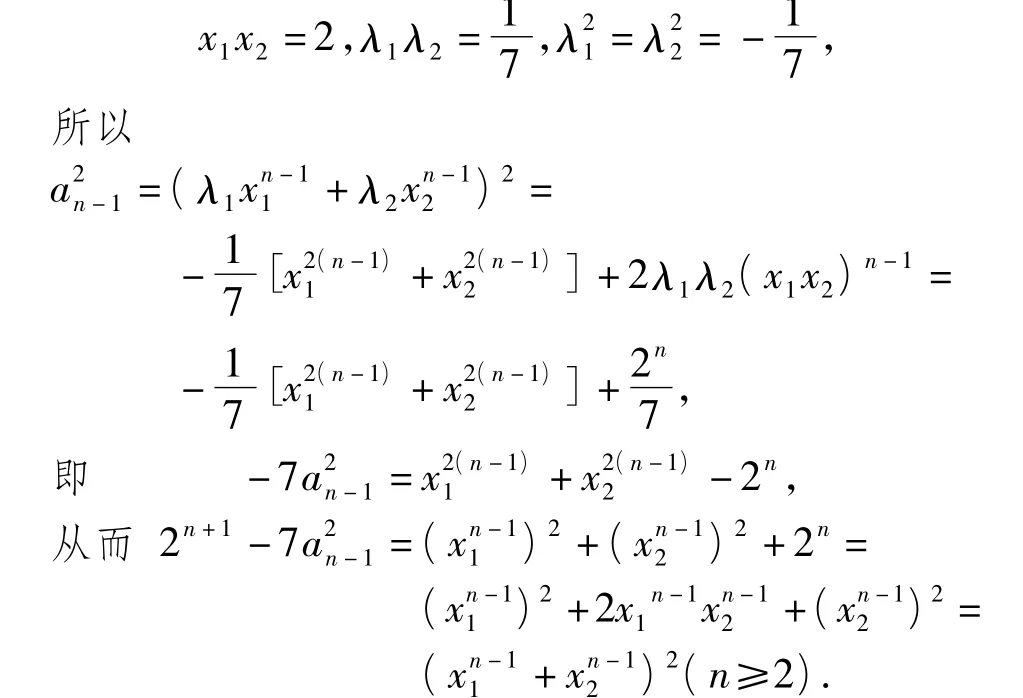
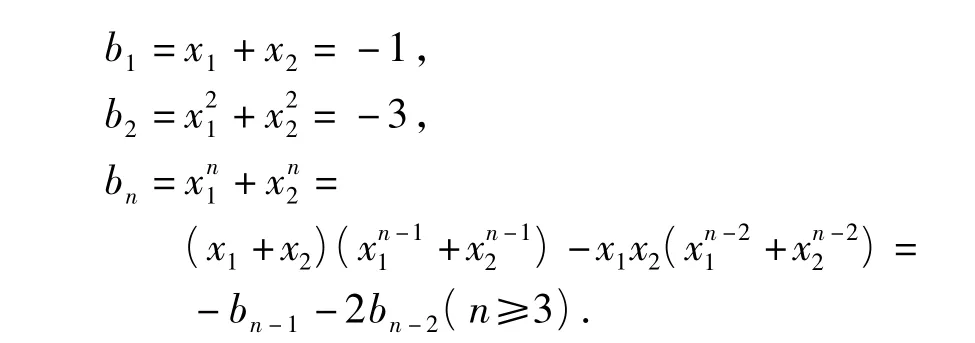
接下来，用数学归纳法证明数列{bn}是整数列.

这就是例3的构造过程，也是例3的一种证明方法.为了进行比较，下面给出另一种证法.

证法2 用数学归纳法易证明 an∈Z(n∈N*)(略).

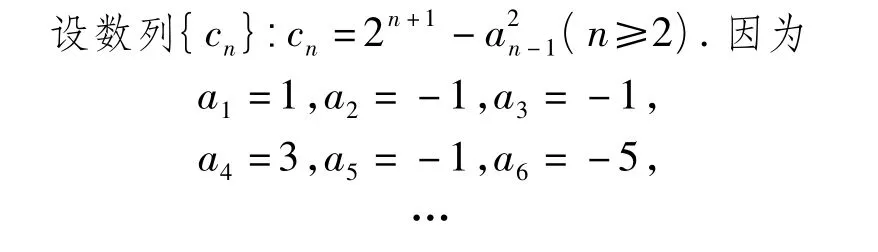
所以数列{cn}的前若干项为

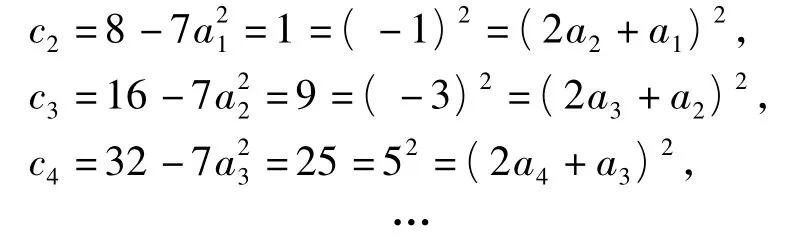
猜想cn=(2an+an-1)2对一切n≥2的自然数n成立.下面用数学归纳法证明.

归纳法的奠基成立.假设当n=k(k≥2)时，

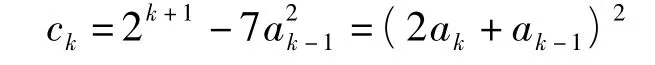
成立，则当n=k+1时，由归纳假设以及式(14)，得

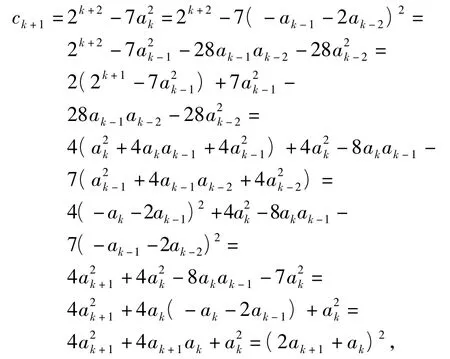
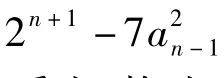
从上面的分析可以看出，构造过程的证明方法(即证法1)：从已知到未知，意图明确，不需要太强的运算技巧;而证法2：从已知⇒未知⇒已知⇒未知，其中当n=k+1时命题成立的证明，运算技巧要求颇高.这2种证明方法留给我们一个命题(留给读者自行证明)：

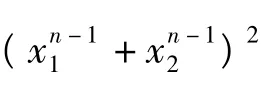
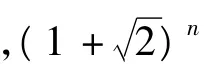
(2012年北约自主招生数学试题)

设x1=1+，它的共轭无理根为x2=1-构造数列从而

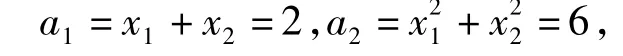
并当n≥3时，有

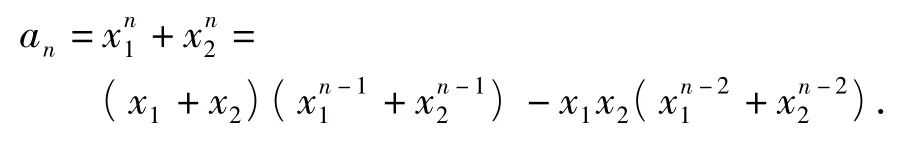
因为x1x2=-1，所以

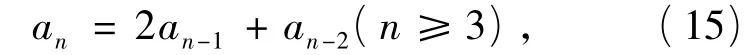
显然由式(15)可知{an}是正整数列，且2|an(n≥1).

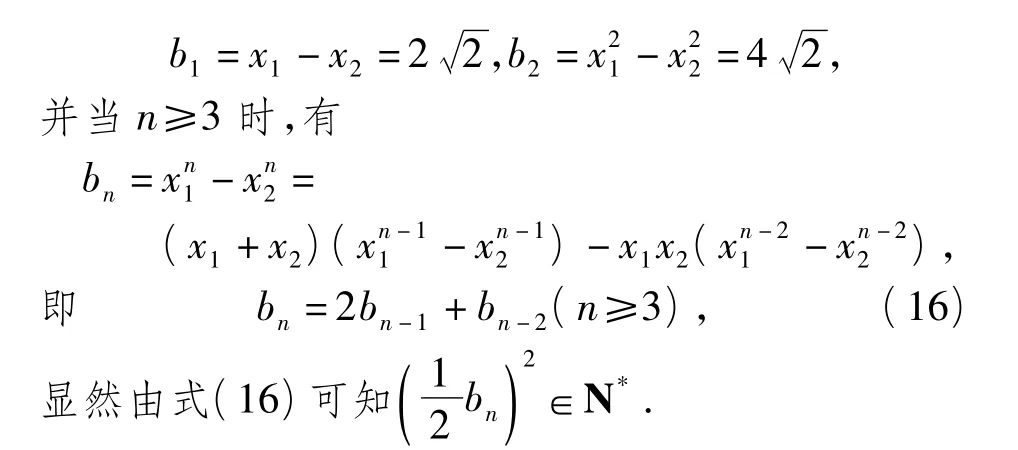
根据构造所得的数列{an}和{bn}，知