一道解析几何题运算教学的实践与思考
2013-08-27崔志荣安丰中学江苏东台224221薛宗华东台市教育局教研室江苏东台224221
●崔志荣 (安丰中学 江苏东台 224221) ●薛宗华 (东台市教育局教研室 江苏东台 224221)
注重运算能力的培养,是我国数学教育“双基”教学的传统特色.但是,近年来,学生的运算能力在下降,突出表现在字母运算、处理多元变量等方面,对于高中生而言,解析几何的运算问题尤为突出.面对这种学习状况,作为一名高中数学教师,怎样在教学中着力提高、逐步培养学生的运算能力呢?
1 一道解析几何题的考情
最近,笔者所任教学校组织了2013届高三学生摸底考试,数学试卷的第19题为:
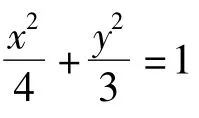
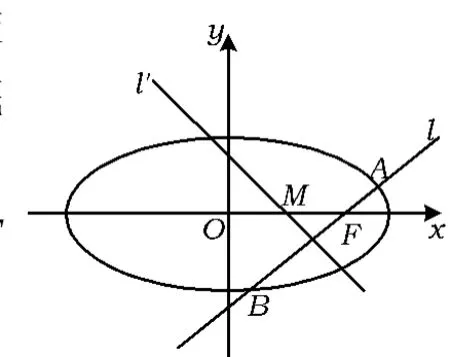
图1
(1)若l的斜率为1,求l'的方程;
考试结束后,笔者发现这道解析几何题并不是特别难,但学生的得分率却非常低.本题满分16分,人均得分约6.5分,从具体的统计数据来看,大部分学生得到了第(1)小题的6分,只有个别学生答对了第(2)小题.于是笔者又对本班学生进行访谈,大部分学生的回答是“第(2)小题我会做,但时间不够,来不及运算,如果再给我10分钟,也许能做对”,还有一部分学生的回答是“这道解析几何题的第(2)小题计算量太大、太复杂,我没有信心算下去”.为此,在试卷评讲中,笔者侧重于对第(2)小题从运算教学的角度作了一些尝试,现整理成文与大家交流.
2 运算教学的课堂实践
教师:本题是解析几何问题,第(2)小题得分率很低,其中一个重要原因是运算能力问题,现在大家都已经看到了这道题的参考答案,本节课我们主要研究第(2)小题的解题运算,哪位同学先来回答一下参考答案的解题思路.
投影展示参考答案(2)设直线AB的方程为

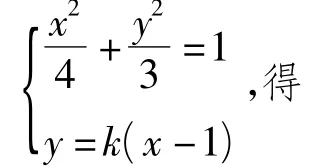

从而线段AB的中垂线方程为

学生1:先联立直线与椭圆的方程,化简得到根与系数的关系,从而求出弦AB的长与AB中点N的坐标,再由AB的中垂线方程解出点M的横坐标,可求出弦FM的长,最终得出结论.
教师:不错,我们把这种方法称之为“代数法之韦达定理”.这样的解题思路容易想到吗?
学生2:容易想到,但却不容易解出答案,运算有些复杂.
教师:学生2说运算有些难,难在哪里?
教师:很好,同学们一定要加强运算能力的训练,只要运算中有一点点失误,就很难得到正确答案.请同学们再思考,还有没有别的办法求弦AB的长,以达到简化运算的目的.
停顿后有学生回答.
学生4:由于AB是过焦点的弦,因此可用焦点弦长公式|AB|=|e(x1+x2)-2a|.
教师:焦点弦长公式怎么推导?
学生5:运用圆锥曲线的第二定义.
教师:先推导焦点弦长公式,再由此求弦AB的长.
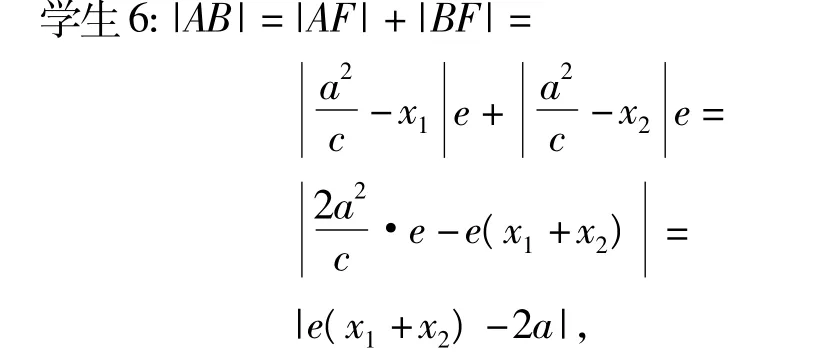
由根与系数的关系,得
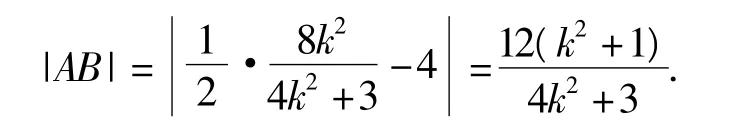
教师:同学们,这样的解答是不是简单多了,那么,求弦FM的长有简化运算吗?
没有学生回答.
教师:对于AB中点N的坐标,可用设而不求的办法吗?
学生7:设N(x0,y0),AB 中垂线方程为
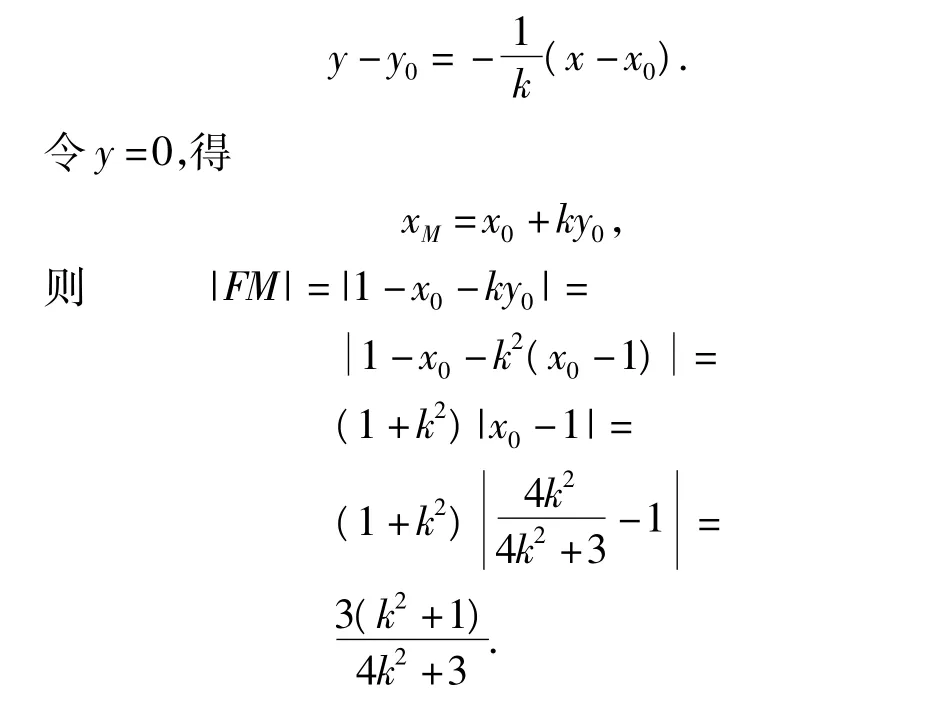
教师:通过优化,我们发现原题的解答运算就不难了,那么是不是参考答案的解答就一无是处呢?
学生8:不是,如果不是焦点弦的问题,那还得按参考答案的方法来求解.
教师:对,我们在处理解析几何问题时,要加强基本运算的训练,如果不是焦点弦,那么还得具备一定的运算能力,当然也要总结方法、比较方法,才能有“巧算”.现在,大家重新思考参考答案的解题思路,看是否有其他方法?
学生9:可以用点差法试试,因为涉及到弦的中点问题.
学生 10:设 A(x1,y1),B(x2,y2),AB 中点N(x0,y0),则

教师:同学们用点差法可顺利求得AB及AB中垂线的斜率,那么如何求弦AB的长与弦FM的长呢?

教师:学生11仍然运用了焦点弦长公式,得到了弦AB的长只与弦AB中点N的横坐标有关,那么怎样求弦FM的长呢?
学生12:AB的中垂线方程为

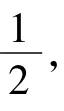

教师:好,下面请同学们来验证一下老师的猜想对不对.请男生用“代数法之韦达定理”完成,女生用“代数法之点差法”完成(目的是加强男生的运算耐心).
教师最后投影展示2组学生代表的解答,并加以点评总结(学生的解答过程与原题的简化运算基本一致,这里不再书写了).
教师:通过本节课的学习,我们在以后的解析几何学习中有哪些需要注意的地方?
学生14:要加强基本运算能力的训练,加强方法的比较,通过分析与比较有时会得到“巧算”.
教师:是的,在学习解析几何时,要重视基本思路、基本运算;要重视分析、比较;要重视过程步骤、针对性训练.这些问题,在我们以后的学习中,还要进一步加强研究.
3 运算教学的几点思考
解析几何作为一种重要的数学思想方法,一直是高考的重点和热点之一,这部分内容也格外受到师生的重视.但一个不容否认的事实是:教师往往感到这部分内容的教学效果不如人意,学生似懂非懂,解题出错率高.结合以上的教学实践,笔者对解析几何的教学有几点思考:
(1)重基本思路,重基础运算.
本文中测试题的参考答案为基本方法,学生容易理解,教学中不可轻视这种基本思路的讲解,但它的运算量偏大,学生不敢动笔,说明基础运算是我们教学中的一个大问题.在平时教学中,如果过于走捷径、用技巧运算,会造成学生眼高手低,基础不扎实,使他们在考场总想容易的方法,那么就容易导致失败.据此,笔者认为在解析几何教学中,要重视基本方法的剖析,淡化技巧方法的讲解,淡化特技运算,重视基础运算.
(2)重分析,重比较.
在解析几何题中,许多题目是有多种解法的,它们的思路不相同,实际运算效果也不一样.因此,在教学中要做到:一是重视思路的分析.比如本文中“代数法之韦达定理”及“代数法之点差法”都是合理的分析方法.二是重视方法的比较.可以看出,这道题目运用韦达定理与点差法处理的运算效果是不同的,如不涉及到弦的中点,点差法就失效,再如,在韦达定理中,用到了焦点弦长公式,若不是焦点弦,则还需要用参考答案的解法.只有通过思路的分析和比较,才能使不同层次的学生有不同的选择,才能使他们更准确地认识问题的本质,才能使他们在解题时游刃有余.
(3)重过程步骤,重针对性训练.
(4)代数方法为主,几何方法为辅.
解析几何的本质是用代数的方法解决几何问题.解题结构为:几何问题到代数问题到代数研究再到几何结果,几何法不应是解析几何的教学重点.有些经验丰富的老教师,知道不少解析几何题的背景,课堂上能把问题一步剖析到简洁的几何方法,讲得很轻松,又无运算量,学生接受得也快,但实际上却是无效的,能有多少学生在考场上知道高考题的背景,很快想到巧妙的几何法?在教学中,还是要脚踏实地用好代数方法,几何方法为辅助,比如圆锥曲线的定义、圆的性质等重要的几何知识可作为辅助使用.
(注:本文是江苏省盐城市教育科学“十二五”规划课题《提高高中学生运算能力的校本研究》的阶段成果.)
