竖向加劲肋对钢板筒仓环向应力影响的研究

2013-08-21李其廉张国良薛荣刚

山西建筑 2013年29期

李其廉张国良薛荣刚

(1.河北科技大学建筑工程学院，河北石家庄 050000;2.北方工程设计研究院有限公司，河北石家庄 050000)

0 引言

钢板筒仓自1968年由德国人利浦发明［1］之后，以其自重轻、建设快、适应性强、便于实现机械化生产等特点在世界各国得到广泛应用。但是目前国内有关钢板筒仓的设计参考资料相对较少，对于具体的钢板筒仓缺乏针对性。当筒仓的直径与高度都较大时，其内壁一般需设置加劲肋。设置加劲肋后钢板受力就会受到加劲肋的影响，《粮食钢板筒仓设计规范》［2］中对于有加劲肋的钢板筒仓可选择下列三种计算方法中任意一种:按带肋壳壁结构，采用有限元方法计算;加劲肋间距不大于1.2 m时，采用折算厚度按薄膜理论进行计算;仓壁或钢结构框架筒仓的钢带水平方向抗拉强度按照公式σf=Phdn/2t≤f进行计算，其中，σf为钢板的环向应力;Ph为储料作用于仓壁单位面积上的水平压力设计值;dn为筒仓内直径;t为仓壁厚度;f为钢板的强度设计值。对于竖向加劲肋对水平向(环向)拉应力的影响如何考虑规范并未作出说明。而实际工程设计时普遍的做法是:计算竖向压应力时，考虑竖向加劲肋和一定宽度的仓壁板宽作为竖向承压构件;计算环向拉应力时，按折算厚度(环向加劲肋间距小于1.2 m时)或仓壁厚度(环向加劲肋间距大于1.2 m时)来计算环向拉应力。而实际工程中有不少大直径钢板筒仓破坏倒塌的事故发生，所以当筒仓直径较大、高度较高时这种方法是否合理，竖向加劲肋是否对钢板环向受力有利，多大间距内有利，目前还没有文献对此进行研究。

本文将针对不同的竖向加劲肋间距对筒仓最大环向应力的影响进行研究。限于篇幅本文仅对存储状态下对结构起控制作用的水平压力荷载进行单工况分析，分析软件采用有限元软件SAP2000［3，4］与 Midas Gen。

1 有限元分析模型

计算简图如图1所示。

筒仓一般由仓顶、仓壁和仓底组成，本文未画出仓顶。水平向加劲肋采用C14，竖向加劲肋采用C12.6，环梁采用C18，仓壁采用统一厚度16 mm。根据钢板筒仓的实际结构特点，作如下模拟计算:筒仓仓壁板按壳单元模拟，筒仓的水平向加劲肋、竖向加劲肋及环梁按梁单元模拟，支座类型为固结。筒壁径向剖分为60段，环向剖分为180段，整个模型包括10 980个节点，10 800个面单元，剖分如图2所示。

2 荷载计算及分析理论

2.1 荷载计算

根据 GB 50322-2011［2］第 4.2.4 条第 1 款规定，确定 Phk:

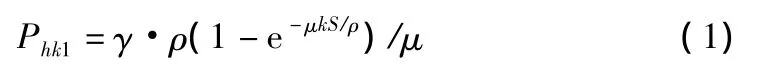
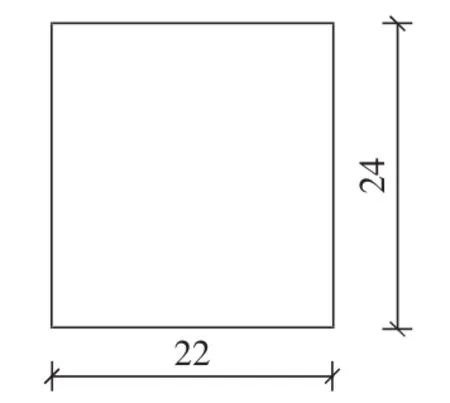
图1 筒仓计算简图（单位：m）

图2 模型网格划分

作用在仓壁单位面积上水平压力设计值:

其中，Phk1，Phk2均为储物作用于仓壁单位面积上的水平压力标准值;Ph为储物作用于仓壁单位面积上的水平压力设计值;γ为储料的重力密度;ρ为筒仓水平净截面的水力半径;μ为储料对仓壁的摩擦系数;e为自然对数的底;k为储料侧压力系数，参考GB 50322-2011附录D表D.1取值;S为储料顶面或储料锥体重心至计算截面的距离;Ch为深仓储料动态压力修正系数，取值参考 GB 50322-2011第4.2.3 条，当 S≤hn/3 时，Ch=1+3S/hn;当S＞hn/3时，Ch=2.0。

计算各参数取值如表1所示。

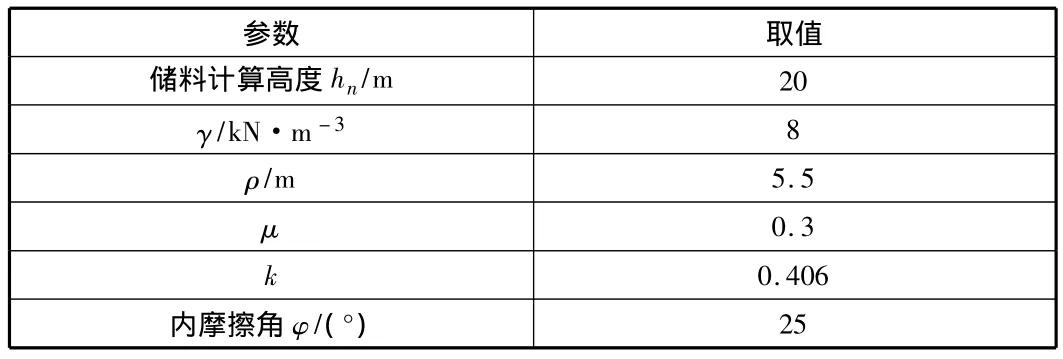
表1 参数取值

2.2 分析理论

有限元法的基本思路和基本原理以结构力学中的位移法为基础，把复杂的结果或连续体看成有限个单元的组合，各单元彼此在节点处连续而组成整体，把连续体分成有限个单元和节点，称之为离散化，先对单元进行特性分析，然后根据各单元在节点处的平衡协调条件建立方程，综合后整体分析［5］。

薄膜理论是假定整个薄壳的所有横截面均没有弯矩和扭矩，而只有薄膜内力的壳体分析理论。圆形结构环向应力计算公式σf=Phdn/2t≤f。该公式是在结构边界没有约束时推导出的理论值。

3 计算结果与分析

作者分别以水平加劲肋间距为 0.4 m，0.8 m，1.2 m，1.6 m，2.0 m，2.4 m，2.8 m;竖向加劲肋间距 0.4 m，0.8 m，1.2 m，1.6 m，2.0 m，2.4 m，3.6 m，4.8 m，6.0 m;并且以水平加劲肋间距一定，竖向加劲肋间距逐渐增大，研究筒仓仓壁最大环向应力的变化规律，并将结果反映在图3～图11中。

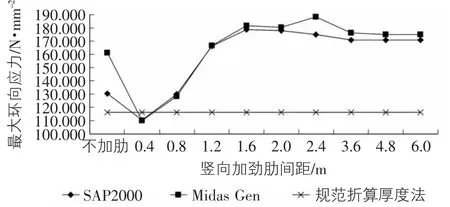
图3 无水平加劲肋时最大环向应力随竖向加劲肋间距的变化

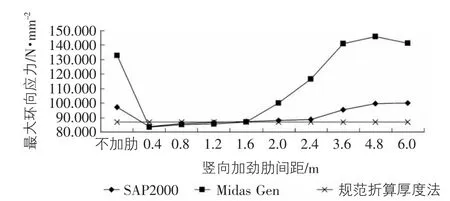
图4 水平加劲肋间距为0.4 m时最大环向应力随竖向加劲肋间距的变化

图5 水平加劲肋间距为0.8 m时最大环向应力随竖向加劲肋间距的变化

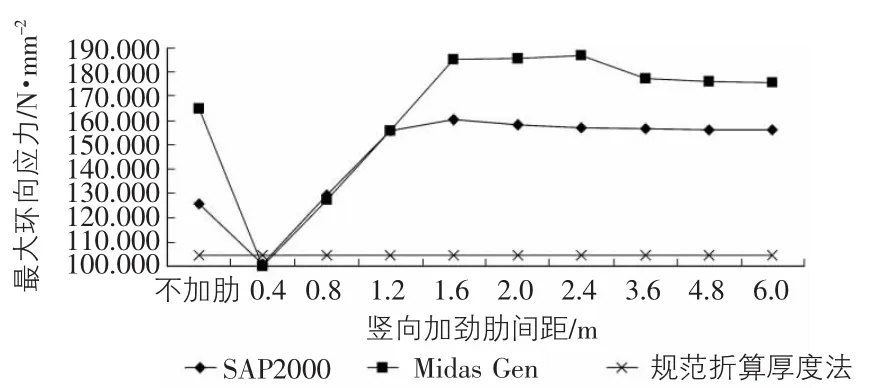
图6 水平加劲肋间距为1.2 m时最大环向应力随竖向加劲肋间距的变化

图7 水平加劲肋间距为1.6 m时最大环向应力随竖向加劲肋间距的变化

图3～图10反映的是在水平加劲肋间距一定，竖向加劲肋间距逐渐增大时的筒仓最大环向应力的变化规律。其中图3和图5～图10中除竖向加劲肋间距为0.4 m外，SAP2000与Midas Gen对筒仓最大环向应力的计算结果均比规范中的折算厚度法计算结果大;当竖向加劲肋间距小于1.6 m时，最大环向加劲肋是随着竖向加劲肋间距的增大而增大;而当竖向加劲肋间距大于1.6 m时，最大环向应力变化已经不明显，说明此时竖向加劲肋的间距对最大环向应力的影响已经很小。

从图4中可以看出竖向加劲肋间距小于1.6 m时，SAP2000与Midas Gen对筒仓最大环向应力的计算结果比规范中折算厚度法的计算结果要小但是比较接近;当大于1.6 m时，SAP2000与Midas Gen的计算结果都比规范中折算厚度法的计算结果要大，并且两个软件的计算结果偏差较大。

从图5中可以看出当竖向加劲肋间距大于0.8 m时，两个软件对筒仓的最大环向应力的计算结果偏差较大，SAP2000的计算结果与规范中折算厚度法较接近。通过图3和图7～图10可以发现水平加劲肋间距为1.6 m，2.0 m，2.4 m，2.8 m 以及无水平加劲肋时最大环向应力随竖向加劲肋间距的变化比较接近，说明当水平加劲肋间距大于1.6 m时，水平加劲肋对筒仓的最大环向应力影响已经很小。

通过图3～图10可以看出当竖向加劲肋间距为0.4 m时，SAP2000与Midas Gen的计算结果都比规范中折算厚度法的计算结果要小，说明当竖向加劲肋间距较小时，竖向加劲肋可以承担一部分环向应力，此时竖向加劲肋的设置对环向受力是有利的。

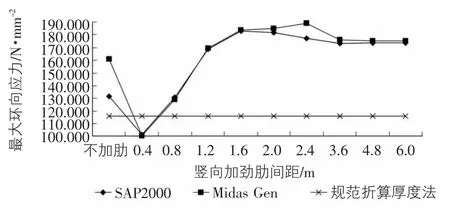
图8 水平加劲肋间距为2.0 m时最大环向应力随竖向加劲肋间距的变化

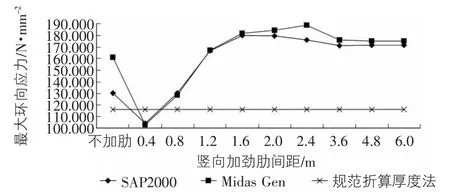
图9 水平加劲肋间距为2.4 m时最大环向应力随竖向加劲肋间距的变化

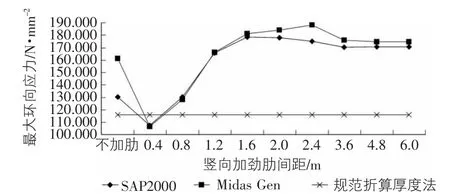
图10 水平加劲肋间距为2.8 m时最大环向应力随竖向加劲肋间距的变化

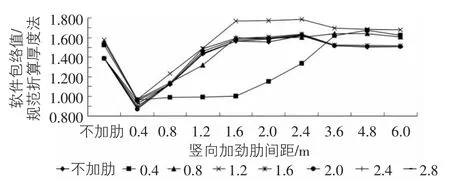
图11 比值随竖向加劲肋间距的变化

图11反映了不同的水平加劲肋间距随竖向加劲肋间距的增大对软件计算结果包络值与规范折算厚度法计算结果的比值(以下简称“比值”)的影响。除水平间距为0.4 m外，其余的变化趋势基本一致。当竖向加劲肋间距小于1.6 m时，比值随竖向加劲肋间距的增大而增大;当大于1.6 m时，比值随竖向加劲肋间距的变化已不明显，说明当竖向加劲肋间距大于1.6 m时竖向加劲肋间距对比值的影响较小，这与图3～图10的分析结果相一致;当竖向加劲肋间距大于0.8 m时，比值均大于1，此时采用折算厚度法设计时，有一定的安全隐患，设计时应当引起注意。水平加劲肋间距为0.4 m时，比值与其余偏差较大主要是因为水平加劲肋的折算厚度较大。