钢筋混凝土土体地下粮仓仓壁结构选型初探
2020-06-05熊晓莉
熊晓莉,都 坤
(河南工业大学土木工程学院,郑州450001)
0 引言
地下粮仓节约占地、造价经济、粮温稳定、储粮安全,从绿色生态储粮安全角度讲,是一种比较理想的仓型。原有的平洞、直洞、喇叭、椭圆、平卧圆柱型等几种地下粮仓仓型在黄土高原、丘陵地区这类地下水位低、土质较硬的地区,有很好的适应性。但在人多地少且地下水位较高的南方地区,上述仓型则不再适用。因此,建造防水防潮性能更好的钢筋混凝土地下粮仓,成为亟待解决的问题。
近些年来,河南工业大学储仓结构团队针对钢筋混凝土土体地下粮仓开展了大量的理论与试验研究。王录民等[1-2]提出了一种新型的“圆筒围成的大空间地下粮仓”,并采用有限元法对其进行了受力和变形分析;郑培等[3]提出了“地下矩形筒围仓”,利用有限元软件分析了整体结构空间相互作用下的结构应力分布及变形;涂成顺[4]利用初参数法和有限元法对地下大直径钢筋混凝土筒仓仓壁的简化计算模型进行了内力和位移分析;付明堂[5]利用有限元法计算了矩形地下粮仓在简化的土压力作用下的位移场和应力场分布规律;熊晓莉等[6]分别采用圆柱壳模型分析法和有限元分析法计算仓壁承载力,研究了钢筋混凝土圆形地下粮仓仓壁承载特性,并分析了仓壁竖向弯矩和环向力分布规律;熊晓莉等[7]在后续的研究工作中,以仓容100t的钢筋混凝土地下试验仓为对象,进行了仓壁侧压力及仓壁结构受力的现场检测试验,通过理论计算与实测结构对比,分析确定了钢筋混凝土地下粮仓仓壁土压力取值方法和仓壁结构受力分析方法。刘海燕等[8]考虑了周围回填二八灰土的实际工况,对圆筒形地下粮仓的浮力大小进行了试验研究。
而国外因粮食储备需求较小,对地下粮仓并未开展相关理论的研究,已建成的地下仓大多以周围岩石作为外层防护[9-11],地下仓建设受地理因素影响较大,仓容较小,未充分利用地下空间,不利于推广应用。
综上所述,国内外的大部分研究工作主要集中于地下粮仓整体结构形式的改进、仓壁结构受力分析及岩体地下仓的推广应用方面,研究对象也多为钢筋混凝土矩形及圆形筒仓,对其他形式的地下粮仓的受力分析较少,且未见有基于弹塑性力学的钢筋混凝土土体地下仓仓体结构选型方面的深入研究。
鉴于钢筋混凝土土体地下粮仓的仓壁自身形状不同将带来受力性能方面的差异,本文将基于弹塑性力学中的平面应变问题求解方法,结合有限元方法分析结果,提出合理的钢筋混凝土土体地下粮仓仓壁的合理结构形式,为钢筋混凝土土体地下粮仓设计提供重要参考。
1 仓壁曲面形式的力学求解
为保证地下粮仓有较好的防水防潮能力,最安全可靠的方法就是要从结构设计角度出发,让地下粮仓尽可能地处于弹性状态。为研究问题的方便,可先采用弹塑性力学中的Von Mises屈服准则做一个简单的判断。若结构某处的Von Mises应力较大,则代表该处应力状态不够理想,材料变形较大,往往是结构容易破坏的地方。
为选择合理的仓壁曲面形式,建立坐标系如图1(a)所示。先假设仓壁曲面的母线为ρ=g(z),如图1(b)所示。若ρ为常数,则母线为直线,仓壁曲面为圆柱筒形。对于内径为R,外径为(R+t)的圆筒,在圆筒内外壁分别受到均布压力f1(z)和f2(z)的作用,如图2(c)所示,圆筒处于轴对称的平面应变状态。
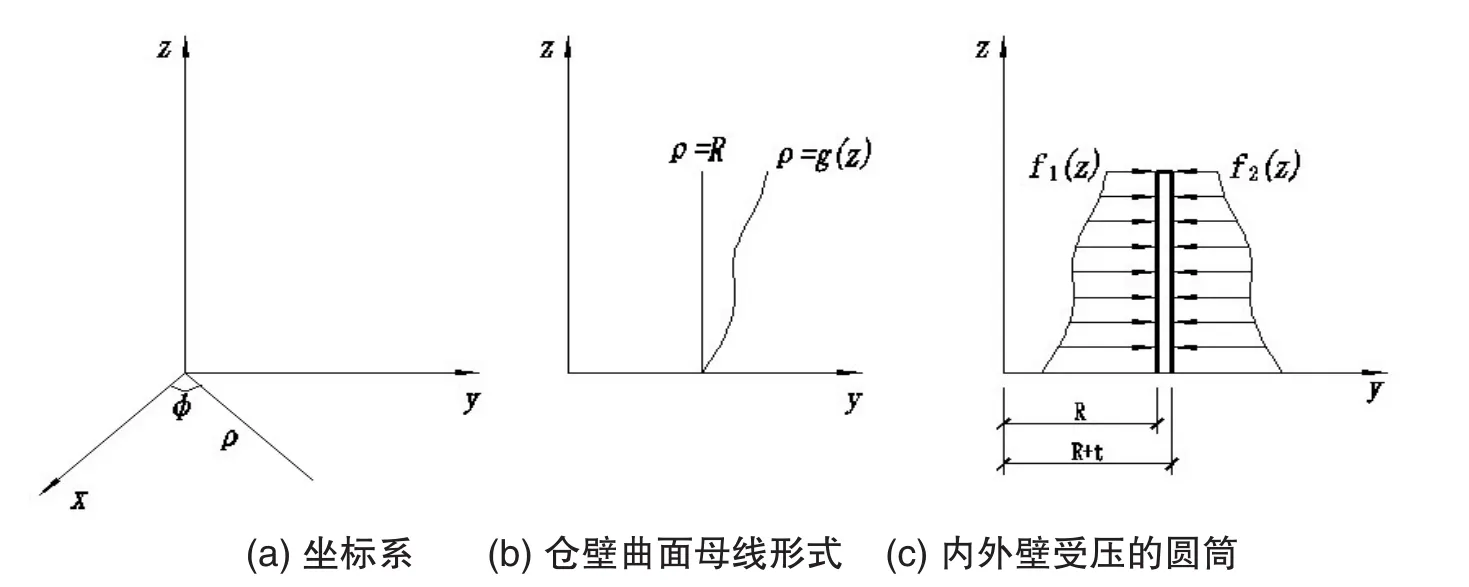
图1 仓壁曲面形式的力学求解模型
由弹性力学的知识可知,平面应变问题的应力分量满足下式:

式中 σρ和σφ为极坐标的正应力分量;τρφ和τρφ为极坐标系的切应力分量;A,C为参数。
考虑边界条件
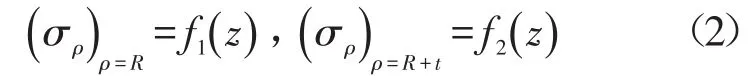
可得

将式(3)和(4)代入式(1),得
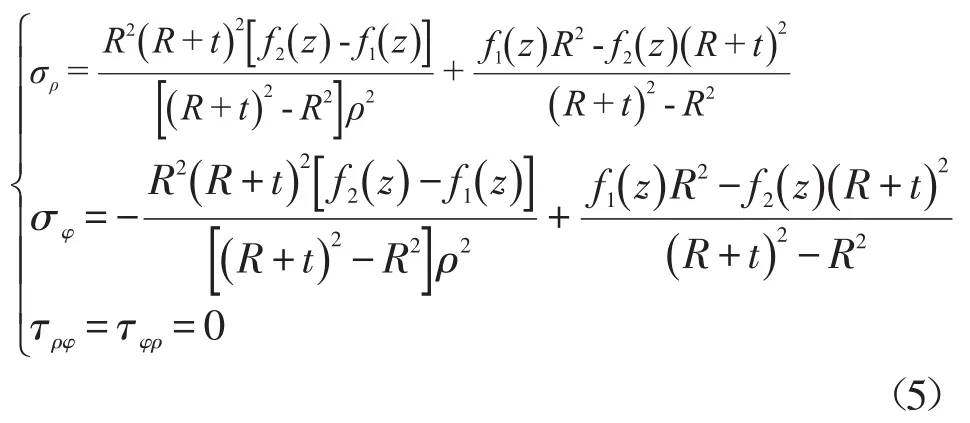
当均布压力f1(z)和f2(z)不大时,整个筒壁处于弹性状态,假定材料是不可压缩的,取v=1/2,则
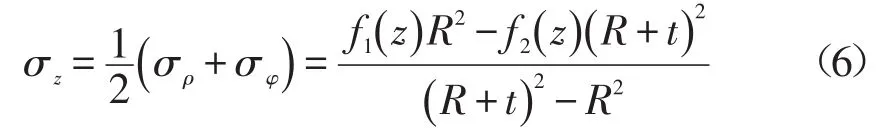
式中σz为柱坐标系的正应力分量。
因为问题是轴对称的,切向应力分量全部为零,所以σρ、σφ、σz就是主应力。按照大小排序,应取σ1=σρ、σ2=σz、σ3=σφ。相应的Mises应力为

对于土体地下粮仓的仓壁而言,均布压力f1(z)为贮料内压,均布压力f2(z)为外部的土压力和水压力,二者沿筒壁z向均为线性分布的面荷载。因此,结合式(7)可知,要使仓壁应力分布均匀且不随仓壁高度大小变化,仓壁曲面母线ρ=g(z)的合理取值应为

式中:m,n为参数。
为后续有限元分析中建立模型的方便,将图1中的空间极坐标系统转化为图2中的平面直角坐标系统。对于仓壁高度为H,仓顶直径为D的土体地下粮仓,要使仓壁应力分布均匀且不随仓壁高度大小变化,仓壁曲面母线建议取抛物线。
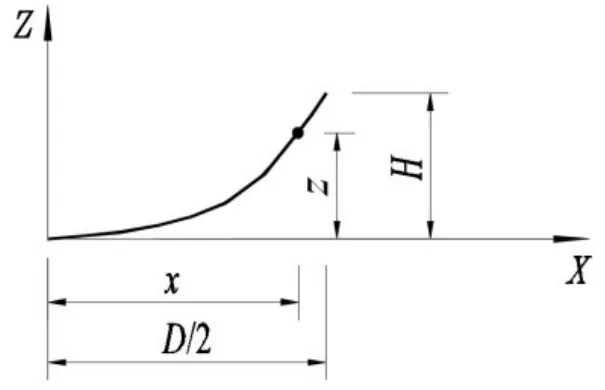
图2 仓壁母线对应的抛物线
由图2中的几何关系可知,该抛物线方程为

仓壁曲面的母线为抛物线,则仓壁曲面为旋转抛物面。因此,建议仓壁结构形式取旋转抛物面。
2 仓壁结构应力的有限元分析
仓壁曲面取旋转抛物面可以保证土体地下粮仓仓壁应力分布均匀且不随仓壁高度大小变化的结论,也可以通过有限元分析的方法加以验证。同时,为了说明旋转抛物面形仓壁与其他常见仓壁形式相比受力更为合理,设计仓容大小近似相等(均为440t)的五种仓型,仓壁形式分别为圆柱筒形、方筒形、圆台筒形、喇叭形以及旋转抛物面形。这五种仓型除几何尺寸不同外,其他的参数取值均相同。
仓容约为440t的五种仓型仅仓壁直径或边长不同:圆柱筒形仓壁直径为10m;方筒形仓壁边长9m;圆台筒形仓壁上/下口直径8m/12m;喇叭形仓壁上/下口直径12m/8m;旋转抛物面形仓壁上口直径14m。其他参数取值为:仓壁高度8m;仓顶、仓壁和仓底厚度均为250mm;环梁尺寸250mm×350mm;仓顶埋深-2.000m,设计地下水位±0.000m;自然填土为砂土(天然重度为16 kN/m3,φ =35°;地下水位以下,饱和重度为20 kN/m3,φ=25°);仓壁混凝土强度等级C35;仓壁钢筋采用HRB400级。
参考文献[6]中的荷载计算方法,各项荷载标准值、分项系数、组合系数及设计值取值如表1所示。除表中数值之外,还需要考虑仓体的自重。因空仓状态结构受力较为不利,计算时不计储料荷载。

表1 仓体荷载标准值、分项系数、组合系数及设计值
利用有限元软件ANSYS对地下粮仓进行受力分析时,选取壳单元SHELL63来模拟仓顶、仓壁和仓底,选取梁单元BEAM188来模拟环梁。钢筋混凝土弹性模量E取30 000MPa,泊松比v取0.2。因研究目的为获得仓壁结构的应力分布,在建模过程中暂不考虑仓顶和仓底的具体结构形式,将仓顶和仓底均简化为平板结构,也不考虑仓顶进粮口的位置和大小。
仓体自重采用施加竖直向上的重力加速度9.8m/s2的方式施加。仓顶荷载和仓底按均布的面载施加,方向由仓外指向仓内;仓壁荷载按沿仓壁高度线性分布的水平面载施加,方向由仓外指向仓内。
支座条件分两种情况:当地下下水位较低时,地下水浮力小于仓体自重,仓体支座位于仓底部位,应在整体结构模型的仓底节点上施加z向约束;当地下水位较高时,地下水浮力大于仓体自重,仓体支座位于仓顶部位,应在整体结构模型的仓顶节点上施加z向约束。对于旋转抛物面形仓壁而言,因只有仓顶和仓壁,仓体支座始终位于仓顶部位。
对五种仓型的有限元模型进行静力求解并显示仓壁应力云图,如图3~图7所示。

图3 圆柱筒形仓壁应力云图

图4 方筒形仓壁应力云图
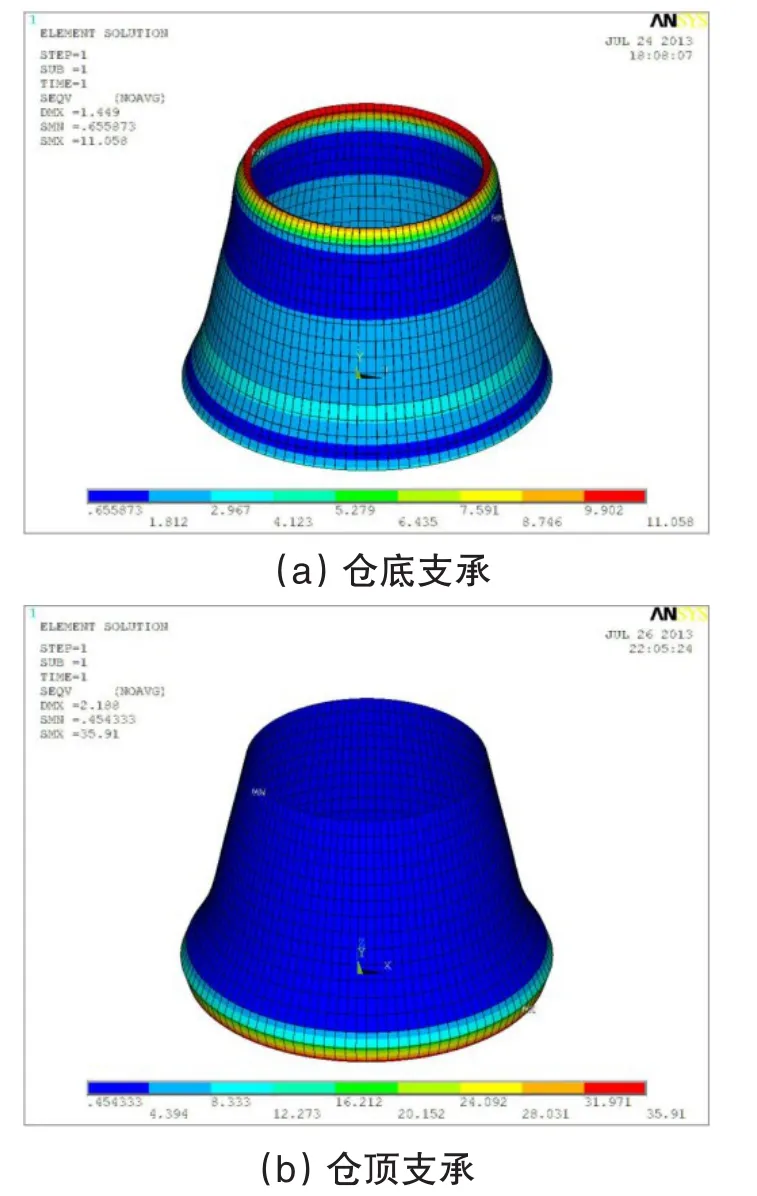
图5 圆台筒形仓壁应力云图

图6 喇叭形仓壁应力云图

图7 旋转抛物面形仓壁应力云图
为对比仓壁应力分析结果,将图3~图7中Von Mises屈服应力大小及分布情况汇总于表2中。由图3~图7及表2中数据可知:
①Von Mises屈服应力最大值不同。应力最大值由小到大的仓壁形式依次为:旋转抛物面形、圆柱筒形、喇叭形、圆台筒形、方筒形。因此,旋转抛物面形仓壁的应力状态相对较好,仓壁上下边缘的变形不大;方筒形则正好与之相反。
②Von Mises屈服应力最大值位置不同。旋转抛物面形仓壁的应力最大值位于仓壁上边缘;其他形式仓壁的应力最大值根据支承位置的不同而异,仓底支承时应力最大值位于仓壁上边缘,仓顶支承时应力最大值位于仓壁下边缘。因此,旋转抛物面形仓壁受力不利的位置仅位于仓壁上边缘,而其他形式仓壁受力不利的位置同时为仓壁上边缘和下边缘。
③Von Mises屈服应力分布情况不同。沿仓壁高度方向,旋转抛物面形仓壁的应力大小变化不大,其他形式仓壁,尤其是方筒形仓壁的应力大小变化较大。因此,旋转抛物面形仓壁的应力状态相对较好,材料的变形沿仓壁高度的变化也比较均匀;方筒形则正好与之相反。
3 仓壁结构内力计算分析
根据Von Mises屈服准则可以对钢筋混凝土土体地下仓仓壁结构受力进行初步的定性研究。为进一步考察仓壁结构的实际受力性能,还需要对仓壁的竖向弯矩和环向力进行计算分析。如果仓壁竖向弯矩较小且环向受压,则仓壁较不易因受力不合理而产生裂缝,且能减少配筋并充分发挥混凝土的抗压承载力,在钢筋混凝土土体地下仓的结构设计中建议优先选用该种仓壁形式。
根据文献[6]和文献[7]可知,仓壁竖向弯矩可按照ANSYS分析所得的仓壁高度方向应力计算获得,计算公式如下:

式中M为仓壁单位长度的竖向弯矩,(kN·m)/m;σze为仓壁外侧z向应力,N/mm2,受拉为正;σzi为仓壁内侧z向应力,N/mm2,受拉为正;W为仓壁单位长度的抗弯模量,mm3。
根据文献[6]和文献[7]可知,仓壁环向力可按照ANSYS分析所得的仓壁高度方向应力计算获得,计算公式如下:
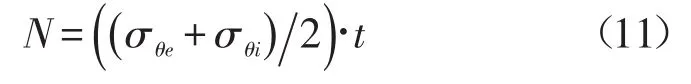
式中N为仓壁单位长度的环向力,kN/m;σθe为仓壁外侧环向应力,N/mm2,受拉为正;σθi为仓壁内侧环向应力,N/mm2,受拉为正;t为仓壁厚度,mm。
根据公式(10)和公式(11)的计算结果,考虑到ANSYS分析模型中支承形式与实际情况尽可能吻合,在进行地下仓仓壁承载力分析时,仓壁受力沿高度H自下而上:0~0.2H范围内取仓顶支承时的计算结果,0.2H~0.8H范围内取仓顶(仓底)支承时的计算结果,0.8H~H范围内取仓底支承时的计算结果[6]。绘制仓壁竖向弯矩沿仓壁高度变化曲线和仓壁环向力沿仓壁高度变化曲线,如图8和图9所示。由图中数据可知:
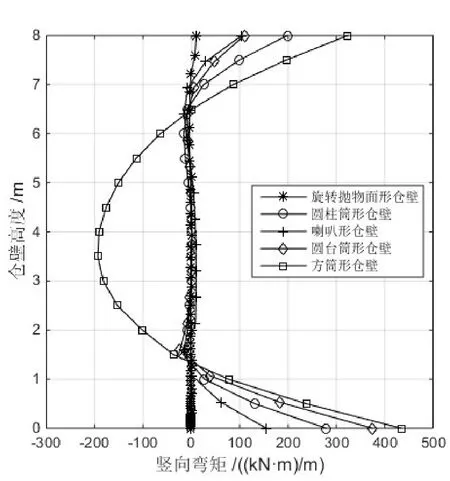
图8 仓壁竖向弯矩对比

图9 仓壁环向力对比
①旋转抛物面形仓壁的竖向弯矩值沿高度变化不大且数值较小;圆柱筒形仓壁、喇叭形仓壁和圆台筒形仓壁的竖向弯矩值在仓壁高度中段变化不大且数值较小,但在仓壁上、下边缘位置处的数值较大,实际工程设计中需重点考虑;方筒形仓壁的竖向弯矩值沿高度变化大,结构受力极不合理。
②旋转抛物面形仓壁的环向力沿高度始终为负值,受力合理;圆柱筒形仓壁、喇叭形仓壁和圆台筒形仓壁的环向力在仓壁中段为压力,却在仓壁上、下0.2H高度范围内为拉力,受力不合理。方筒形仓壁的环向力虽然始终为负值,但因前述仓壁竖向弯矩分布不合理,亦不推荐使用。
综上所述,钢筋混凝土土体地下仓仓壁结构选型可按照如下原则进行:
①仅从受力角度考虑,旋转抛物面形仓壁受力最为合理。但现阶段因其施工难度较大,且无合适的进出粮工艺可参考使用,暂未推广。在解决施工难度和进出粮工艺的前提下,建议推广使用该仓型。
②圆柱筒形仓壁和喇叭形仓壁因施工方便、受力合理且相应形式的地上仓体的设计方法成熟,现阶段可将其作为一种土体地下粮仓的主流仓型进行推广应用。在设计过程中,需注意仓壁上、下边缘处的竖向抗弯问题和仓壁上、下0.2H高度范围内的环向抗拉问题。
③圆台筒形仓壁受力性能一般,且因仓壁上口小、下口大,施工难度较大,不建议选用。
④方筒形仓壁结构受力极不合理,且在环梁与角柱处容易产生应力集中,因此,当土体地下粮仓仓容较大时,不建议选用。
4 结论
合理选择钢筋混凝土土体地下粮仓的仓壁结构形式,对地下粮仓结构选型而言意义重大。
基于弹塑性力学中的平面应变问题,推导出了仓壁曲面的母线方程,分析获得“要使仓壁应力分布均匀且不随仓壁高度大小变化,仓壁曲面母线建议取抛物线,即建议仓壁结构形式取旋转抛物面”的结论。
为验证上述理论推导结果的正确性,选取仓容近似相等的五种仓型,仓壁形式分别为圆柱筒形、方筒形、圆台筒形、喇叭形以及旋转抛物面形,利用有限元方法进行受力分析后发现:受力最为合理的是旋转抛物面形仓壁,其应力最大值较小且分布均匀,竖向弯矩值沿高度变化不大且数值较小,环向始终受压,因该种仓壁结构形式受力合理,在解决施工难度和进出粮工艺的前提下,建议推广使用该仓型;圆柱筒形仓壁和喇叭形仓壁因施工技术成熟且受力较为合理,现阶段可作为土体地下粮仓的主流仓型进行推广应用;圆台筒形仓壁受力性能一般,且施工难度较大,不建议使用;方筒形仓壁的受力极不合理,在大型的土体地下粮仓中不建议选用。
上述研究工作仅从结构受力角度考虑仓壁结构的选型的问题,尚未考虑到施工的难易程度、进出粮工艺的配合以及工程造价等因素的影响。此外,仓顶和仓底结构形式的变化对仓壁受力性能的影响也是需要进一步深入探讨的问题。
