装配式地下粮仓钢板-混凝土组合仓壁整体结构力学性能分析

王振清，侯支龙，揣 君，张庆章，张 昊

河南工业大学 土木工程学院，河南 郑州 450001

地下粮仓(以下简称地下仓)与地上粮仓相比具有低温减损、生态环保、节能节地等显著优势[1]。目前，大直径钢筋混凝土地下仓克服了早期地下仓受土质和地形条件限制、仓容小、机械化程度低等缺点，被认为是我国地下仓建设潜在的发展方向[2-4]。然而，钢筋混凝土地下仓也存在一些关键问题亟待解决，如施工工期长、造价高、防水性能差[5-6]，这些问题将制约其今后的推广应用。

装配式技术和组合结构技术在工程领域的应用越来越普遍。装配式建筑具有工业化水平高，减少现场湿作业，并减少建筑垃圾和污染等优点，在欧美、日本等国家和地区取得了广泛的应用[7-8]。在国内地下工程中，尤其是在隧道和地铁工程中应用已十分普遍[9-11]，在地下仓中采用装配式技术具有广阔的前景。组合结构具有承载力高、刚度和延性大、施工方便等优势，已大量应用于大跨度桥梁和高层、超高层建筑结构中[12-13]。圆形地下仓由于受到水土压力、水浮力、粮食压力等多种作用，承载特性复杂[14]。采用组合结构，能够充分发挥其刚度大、承载力高的优势。此外，钢板的防水性能良好[15-16]，可以解决地下仓中的防水难题。

文献[17]采用装配式技术和组合结构技术，提出了一种新型装配式地下仓结构方案。文献[18]提出了 “等同原理”仓壁接头设计方法，并对单个仓壁接头的力学性能进行了足尺试验和有限元分析，结果表明装配式仓壁试件和无接头仓壁试件力学性能相近，装配式仓壁的结构计算可等效为现浇一体无接头仓壁的结构计算。但这种等效的设计方法并没有对装配式组合仓壁整体结构进行分析。

作者基于等同原理的设计方法，设计了装配式仓壁竖向直口接头和环向榫形接头。由于新型装配式地下仓直径和深度较大，不易开展现场实仓力学性能试验。为此，利用有限元软件ABAQUS建立装配式钢板-混凝土组合仓壁与无接头钢板-混凝土组合仓壁整体结构有限元模型，对比分析两者在空仓工况下的受力特点。在有限元分析基础上，基于柱壳理论给出了装配式钢板-混凝土组合仓壁位移和内力简化计算式，为装配式地下仓仓壁的设计计算提供参考。

1 装配式地下仓仓壁接头设计

接头是装配式结构最薄弱的部位，其可靠性是装配式结构的关键。装配式结构接头的主要方式有钢筋套筒灌浆接头和钢筋浆锚搭接接头[19]。文中地下仓仓壁采用钢板-混凝土组合结构，仓壁预制块之间存在沿仓体环向和竖向的接头，防水要求高，加之是地下施工，无论是采用钢筋套筒灌浆接头，还是钢筋浆锚搭接接头，施工难度高，质量难以控制。由柱壳理论可知，仓壁在外部水土压力作用下，主要为环向受压，沿仓壁高度方向受力较小。即沿仓壁高度方向的竖向接头受力较大，沿仓壁水平方向的环向接头受力较小。若仓壁环向接头满足构造要求，在计算时可以忽略环向接头处的影响。仓壁竖向接头采用“等同原理”的设计方法，即带竖向接头仓壁的强度和刚度不弱于现浇一体无接头仓壁。

仓壁竖向接头构造及尺寸如图1所示。接头采用直口的接头形式，由U型包边钢板、工字钢桩、传力钢板和止水钢板组成。包边钢板通过栓钉和仓壁混凝土预制在一起，钢桩、传力钢板、止水钢板分别与包边钢板采用焊缝连接。竖向接头尺寸根据文献[18]中组合仓壁竖向接头处截面的抗弯刚度与非接头处截面的抗弯刚度比得到。仓壁横截面示意图如图2所示，t表示厚度，xs、xc分别表示钢板、混凝土中轴到组合截面形心轴的距离，x1、x2、x3分别表示止水钢板、传力钢板、钢桩下翼缘中轴到截面形心轴的距离，H为横截面总高度，b为横截面宽度，a为传力钢板与钢桩下翼缘的中轴距离。接头处忽略工字钢桩腹板和上翼缘板对抗弯刚度的影响。组合仓壁非接头处截面、接头处截面的抗弯刚度分别用D1、D2表示。

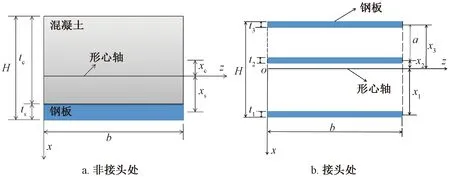
图2 仓壁横截面示意图Fig.2 Section diagram of silo wall

D1=E1I1+E2I2，

(1)

D2=E2I3，

(2)

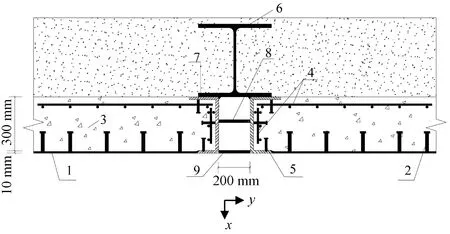
1.内侧钢板 2.栓钉 19 mm 3.混凝土 4.钢筋网片 φ8 mm@150 mm 5.栓钉 φ13 6.钢桩HW400×400×13×21 7.包边钢板厚16 mm 8.传力钢板厚18 mm 9.止水钢板厚18 mm图1 仓壁竖向接头构造及尺寸Fig.1 Construction and dimension of vertical joint of silo wall

式中：E1、E2为混凝土和钢板的弹性模量，MPa；I1、I2为非接头处混凝土和钢板截面对组合截面形心轴的惯性矩，m4；I3为接头处3块钢板截面对形心轴的惯性矩之和，m4。

对于组合仓壁非接头处截面形心轴，定义混凝土截面面积对Z轴的静矩为N1，钢板截面面积对Z轴的静矩为N2，则有：

(3)

可求得：

(4)

对于组合仓壁接头处截面形心轴，由材料力学形心公式可知：

(5)

可求得:

(6)

图3为仓壁环向接头示意图，仓壁预制块环向接头采用“榫形”对接，接头预制构件两端设置凸榫(仓内侧上端凸)，并在预制构件接触面设置柔性止水材料，仓内侧通过止水钢板与内包钢板焊接，形成完整封闭的钢板防水层。

图3 仓壁环向接头示意图Fig.3 Schematic diagram of ring joint of silo wall

2 有限元分析

2.1 有限元模型建立

装配式地下仓的结构方案基于目前正在建设的地下仓，基本情况：仓顶覆土深约1.5 m，仓内有设备隔层；仓内径25 m，仓壁厚0.31 m，顶板厚0.4 m，底板厚0.6 m。仓底板(漏斗状)标高-19～-15 m，组合仓壁高为15.1 m，周围均布36根钢桩，钢桩的型号为HW400×400×13×21。

按照地下仓结构方案及接头尺寸，利用有限元软件ABAQUS建立装配式地下仓和无接头地下仓整仓模型，如图4a、4b所示。装配式地下仓模型忽略环向接头，竖向接头有限元模型如图4c所示。参考文献[18]装配式钢板-混凝土组合仓壁试件的建模方法，仓壁钢板和混凝土采用刚性连接，接头处钢板和钢板也采用刚性连接。仓壁混凝土采用实体单元，仓壁钢板采用壳单元，仓顶板、仓底板、内筒采用壳单元，仓顶群梁采用梁单元。仓顶板与内筒之间、仓底板与内筒之间、仓顶板与仓壁之间、仓底板与仓壁之间均设置为刚接。装配式地下仓模型和无接头地下仓模型沿仓壁高度方向为Z向，并对仓壁底部设置Z向约束。

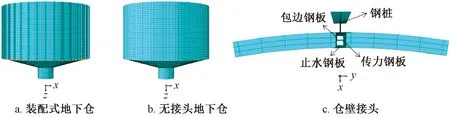
图4 有限元模型及边界条件Fig.4 Finite element model and boundary conditions

2.2 模型参数

模型中混凝土等级为C40，弹性模量为3.25×104MPa，泊松比为0.2。钢板型号为Q345，弹性模量为2.06×105MPa，泊松比为0.3。根据GB 50010—2015《混凝土结构设计规范》，混凝土轴心抗压强度设计值为19.1 N/mm2，抗拉强度设计值为1.71 N/mm2。钢板抗拉和抗压强度设计值均为310 N/mm2。

该装配式地下仓为地下薄壁圆筒结构，在外部水土压力下，空仓状态是最不利工况。由经典土压力公式计算得到外部水土压力，仓壁顶部、仓壁底部最大荷载标准值分别取65、300 kN/m2。

2.3 有限元结果及分析

2.3.1 仓壁位移

图5为装配式地下仓和无接头地下仓仓壁在空仓工况下的位移云图。可见在外部水土压力荷载下装配式仓壁和无接头仓壁均发生径向位移，位移最大值分别为3.16 mm和3.32 mm。装配式仓壁与无接头仓壁位移相对差为4.82%，表明设计的装配式仓壁具有与无接头仓壁相匹配的刚度，且不弱于后者。

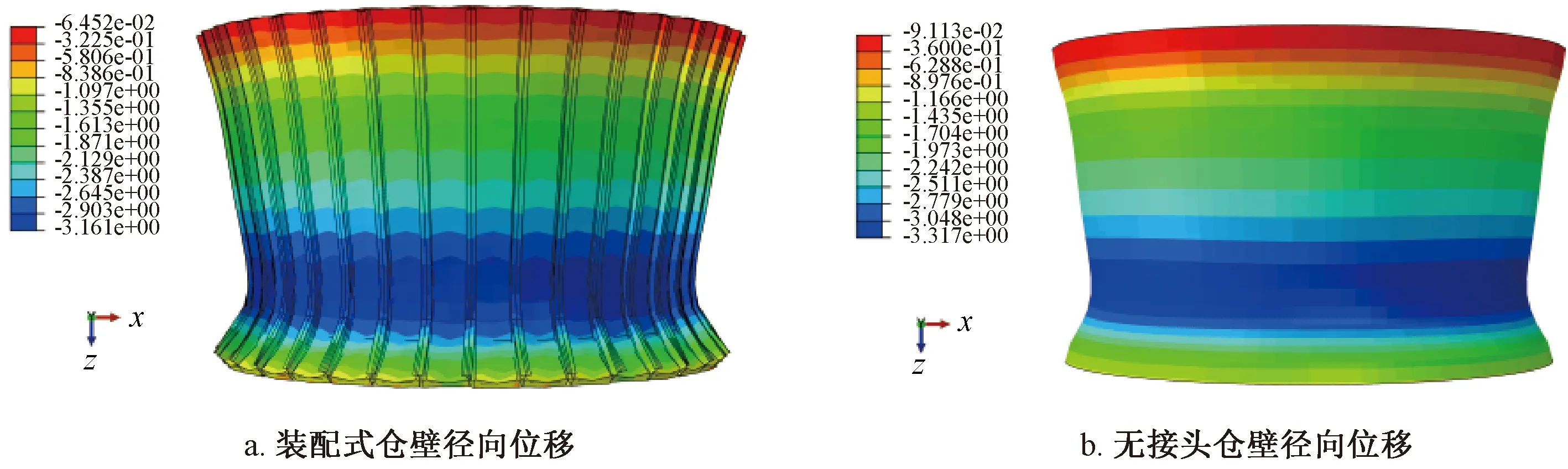
图5 仓壁位移云图Fig.5 Displacement nephogram of silo wall

地下仓仓壁沿高度方向的径向位移分布如图6所示，可以看出装配式仓壁与无接头仓壁径向位移变形趋势相同，位移值均为先增大后减小。装配式仓壁在靠近仓底1/5壁高处径向位移达到最大值，无接头仓壁在靠近仓底1/4壁高处径向位移达到最大值，接头的存在使仓壁位移最值位置向仓底移动。

图6 仓壁径向位移分布Fig.6 Radial displacement distribution of silo wall

2.3.2 仓壁应力

图7为装配式仓壁与无接头仓壁混凝土应力分布。可以看出混凝土环向应力为压应力(拉应力为正)，Z向应力整体以压应力为主(拉应力为正)，仓壁底部和顶部局部承受拉应力。装配式仓壁与无接头仓壁压应力均满足混凝土轴心抗压强度设计值，无接头仓壁底部Z向应力最值超过混凝土抗拉强度设计值，但仅是局部超限，实际工程中可通过配置环梁和受拉钢筋使其满足强度要求。由图7a可知，装配式仓壁与无接头仓壁混凝土环向应力沿仓壁高度方向变化趋势相同，均为先增大后减小。两者应力最大值发生在距离仓底1/5仓壁高度处。图7b中装配式仓壁与无接头仓壁混凝土Z向应力分布曲线吻合较好，仓壁底部因接头存在应力值有所差异，但影响范围较小。

图7 仓壁混凝土应力分布Fig.7 Stress distribution of concrete of silo wall

图8为装配式仓壁与无接头仓壁钢板应力分布。可见钢板环向应力为压应力(拉应力为正)，Z向应力以压应力为主(拉应力为正)，在距离仓底1/6仓壁高度处出现局部拉应力。装配式仓壁与无接头仓壁钢板承受的拉应力和压应力均满足钢板抗拉和抗压强度设计值。由图8a可知，装配式仓壁与无接头仓壁钢板环向应力变化趋势相同，沿仓壁高度方向应力先增大后减小，装配式仓壁钢板环向应力值整体稍小于无接头仓壁钢板应力值。图8b中装配式仓壁与无接头仓壁钢板Z向应力分布曲线吻合较好，由于接头的存在，装配式仓壁底部钢板Z向应力小于无接头仓壁。

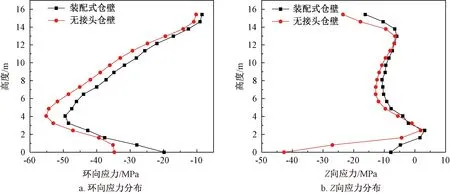
图8 仓壁钢板应力分布Fig.8 Stress distribution of steel plate of silo wall

对比装配式仓壁和无接头仓壁混凝土与钢板的应力分布，接头的存在虽使仓壁应力有所变化，但整体变化不大。

3 装配式地下仓仓壁位移与内力简化计算

由有限元结果对比分析可知，装配式仓壁与无接头仓壁在相同荷载下，应力值和位移值沿仓壁变化趋势相同，具有相匹配的强度与刚度，仓壁接头等同原理的设计方法对仓壁整体结构是适用的。为促进装配式地下仓的推广应用，有必要对其计算式简化。地下仓结构设计现无规范可依，装配式仓壁由于接头的存在使计算更复杂，因此采用圆柱壳理论对无接头仓壁进行计算，计算位移与内力等效为装配式仓壁。

无接头仓壁由钢板和混凝土两种材料组成，混凝土厚h1=300 mm，钢板厚h2=10 mm，栓钉可使其协同工作，采用换算截面法换算成一种材料，等效刚度D1=1.21×1011N·mm，等效计算半径R=12.63 m，仓壁计算高度L=15.1 m。由于有限元模型中考虑了仓顶和仓底对仓壁的约束，此约束弱于固结，但整体影响不大。为简化计算，仓壁支撑上下端按固结考虑，荷载大小与有限元施加的荷载相同。

三角形荷载(q)作用时，根据无矩理论，可得柱壳中面的径向位移和转角。

(7)

(8)

式中:w1为径向位移，mm；θ1为转角，rad；E为等效弹性模量，MPa;h为等效仓壁厚度，mm。

由于仓壁顶端和底端为固定支撑，有弯矩(M)和剪力(Q)存在，由文献[20]可知，圆柱壳一端在弯矩和剪力作用下有径向位移。

(9)

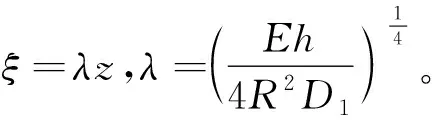
根据固定端总径向位移和总转角为零，可求得弯曲内力。

(10)

(11)

将式(10)、式(11)代入式(9)，可得在M、Q作用下柱壳中面的径向位移(w2)。

(12)

再将柱壳中面径向位移代入竖向弯矩(Mv)和环向轴力(Nc)。

(13)

(14)

有矩理论相应的竖向弯矩(Mv1)和环向轴力(Nc1),如式(15)和式(16)所示。

(15)

(16)

在矩形荷载(p)作用下，由无矩理论可得柱壳中面的径向位移(w3)和转角(θ2)。

(17)

θ2=0。

(18)

在M、Q作用下柱壳中面的径向位移(w4)。

(19)

相应的内力：

(20)

Nc2=-pRe-ξ(cosξ-sinξ)+

(21)

式中：β=λ(L-z)。

在外部水土压力作用下，得到壳中面的总径向位移及内力。

w=w1+w2+w3+w4，

(22)

Mv=Mv1+Mv2，

(23)

Nc=Nc1+Nc2。

(24)

图9为仓壁径向位移理论值与模拟值的对比，可以看出理论值与模拟值沿仓壁高度变形趋势相同。理论值得到的仓壁最大径向位移较模拟值稍大，与装配式仓壁模拟值和无接头仓壁模拟值相对差分别为12%和7.78%。仓底位置径向位移模拟值较大，这是由于有限元模型中仓底板对仓壁的约束弱于固结，但这种影响只是局部的。

图9 仓壁径向位移对比Fig.9 Comparison of radial displacement of silo wall

将理论计算和有限元计算得到的仓壁竖向弯矩和环向轴力沿仓壁Z向绘制成曲线，如图10和图11所示。其中，有限元仓壁Z向应力和环向应力按文献[14]中方法转化为仓壁竖向弯矩和环向轴力。

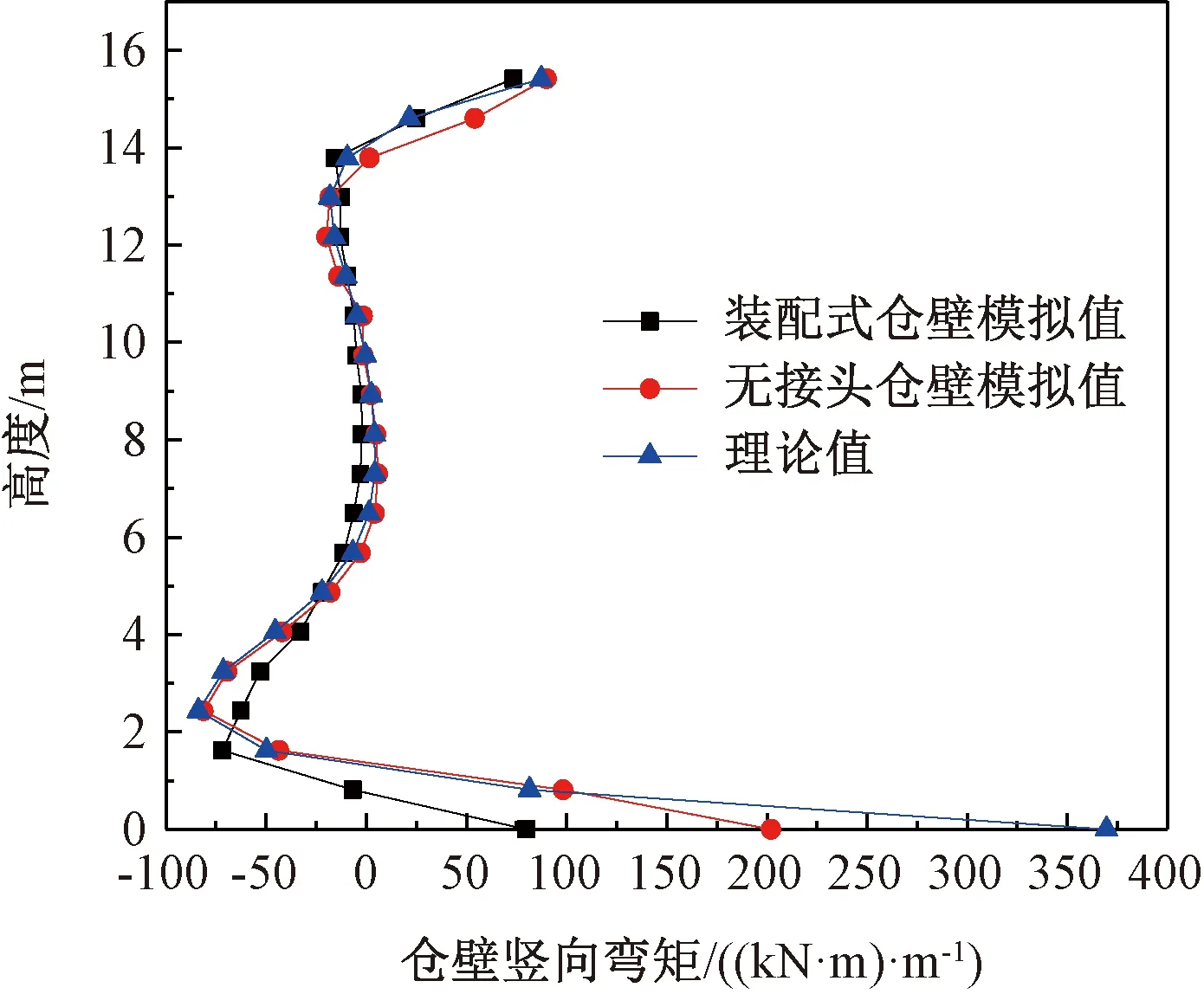
图10 仓壁竖向弯矩对比Fig.10 Comparison vertical moment of silo wall

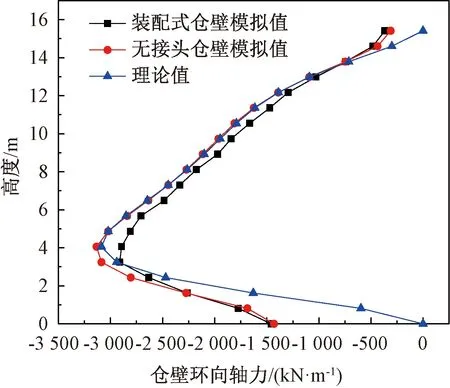
图11 仓壁环向轴力对比Fig.11 Comparison of annular axial force of silo wall

Mv=(σzi-σzj)/2×W×10-6，

(25)

式中：Mv为仓壁单位长度的竖向弯矩，外侧受拉为正，( kN·m)/m;σzi、σzj分别为仓壁外侧和仓壁内侧的Z向应力，受拉为正，MPa；W为仓壁单位长度的抗弯模量，mm3。

Nc=(σci+σcj)/2×h，

(26)

式中：Nc为仓壁单位长度环向轴力，受拉为正，kN/m；σci、σcj分别为仓壁外侧和内侧的环向应力，受拉为正，MPa。

由图10和图11可知，理论值与有限元模拟结果整体吻合较好。在水土压力作用下，仓壁承受的竖向弯矩相对较小，主要为环向受压，有限元得到的装配式仓壁和无接头仓壁最大环向轴力分别为-2 911.78、-3 133.01 kN/m，与理论值得到的仓壁最大环向轴力-3 085.99 kN/m相对差分别为5.65%和1.52%，理论计算具有较好的预测精度。采用简化计算可以较好地吻合装配式仓壁的位移和内力，且偏于安全，为装配式地下仓仓壁的设计计算提供参考。

4 结论

基于等同原理的设计原则，提出了一种新的装配式地下粮仓仓壁竖向接头和环向接头。在最不利工况下，有限元法得到的装配式仓壁和无接头仓壁变形和受力性能相近，装配式仓壁最大径向位移为3.16 mm，无接头仓壁最大径向位移为3.32 mm，相对差为4.82%，装配式仓壁接头采用等同原理的设计原则对仓壁整体结构是适用的。简化计算方法得到的理论值与有限元法得到的装配式仓壁和无接头仓壁模拟值吻合良好，理论值中仓壁最大环向轴力与模拟值中装配式仓壁和无接头仓壁最大环向轴力相对差分别为5.65%和1.52%，采用这种简化算法可以较好地预测装配式钢板-混凝土组合仓壁的内力和位移，为结构设计计算提供依据。