线弹性静力问题的Fourier谱元法初探

史玉洁

(山西省中部引黄工程建设管理局，山西太原 030000)

0 引言

谱方法是一种结合谱方法和有限元思想来求解偏微分方程的数值方法，它的最大优点在于具有“无穷阶”的收敛性，适当的谱方法所求得的近似解以N－1次的收敛速度逼近精确解［1］，N代表选取的基函数的个数，这一点是有限元法无法比拟的;并且谱方法采用的插值函数(如Fourier级数、Legendre多项式、Chebyshev多项式)具有无限可微的性质，相对于有限元法采用的有限次可导多项式作为插值函数的方法，具有显著的精度优势［2］。

借助有限元中等参元的思想，Patera［3］结合谱方法的精度于1984年提出了谱元方法(SEM)。近年来，谱方法已被成功地应用于求解各种实际问题。Usik Lee等［4］将Fourier谱方法运用到一些梁结构动力分析中，通过谱元法与解析解以及有限元方法结果的对比证明了谱元法的高精度，M.Krawczuk等［5］讨论了有缝的Timoshenko梁动力分析的 Fourier谱元法，Dimitri Komatitsch等［6］在考虑大地模型的异质性的情况下用谱方法模拟地震波的传播，国内林伟军，秦国良等［7，8］长期从事研究弹性波传播模拟的Chebyshev谱元法。

本文利用离散傅里叶逼近的方法对未知函数逼近，借助有限元法中等参单元的思想，在坐标变换的时候同样采用傅里叶谱逼近的方法，可推导出谱元法中单元刚度矩阵kei的形成过程，在此基础上编制而成的谱元法计算程序，能够较好的求解线弹性静力问题。通过数值算例，对比谱元法与有限元方法的计算精度，能得到令人满意的结果。

1 函数的Fourier谱近似

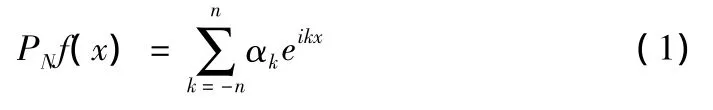
其中，

f(x)的傅里叶展开式可以由以下推导:

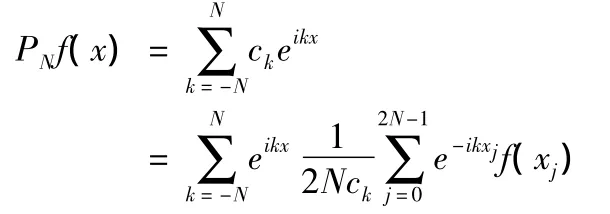
其中，

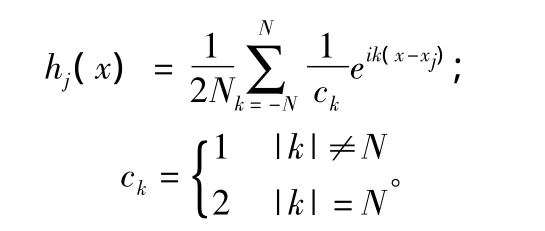
在傅里叶谱方法中，节点的选取有以下选择:

在实际应用中，式(2)是最常被采用的。

对三维函数u(ξ，η，ζ)，在标准的正方体单元内，分别定义ξ，η，ζ三个方向上的节点系{ξj}，{ηk}，{ζl}(见图1)。

图1 正方体单元

弹性静力计算中的基本未知量位移u(ξ，η，ζ)的傅里叶谱展开式为:

其中，

在单元内若节点(ξj，ηk，ζl)对应的单元节点编号为 i，则我们记 Njkl=hj(ξ)hk(η)hl(ζ)，则式(5)可以表示为:

其中，N+1等于单元内总节点数目;Ni为Fourier谱近似情况下，反映单元的位移形态，即单元位移的形函数。可以将它代入后，形成在傅里叶谱近似下的形函数矩阵N。需要注意的是，本节中的谱近似直接是在标准的正方形单元中进行的，其ξ，η，ζ三个方向跨度区间均为(0，2π)。显然在实际计算中是不可能全部得到这样理想的单元的，因此同有限元方法一样，谱元法也要对单元进行等参化处理。

2 分布函数

有限元方法通过坐标变化将原来的不规则边界单元转化为标准单元，通过形函数将原有坐标系(x，y，z)和新的坐标系(ξ，η，ζ)建立一一对应的关系，将原来整体坐标系变换成新的各个单元下的局部坐标系，在标准单元内的计算提高计算的速度。如果坐标变换和函数插值采用相同的节点和相同的插值函数，则称此为等参单元。

谱元法利用了有限元单元划分以及等参化的思想，不同的是Fourier谱元法选取Fourier多项式的极值点作为配置点，形函数选用的是具有无穷阶可微性质的谱展开式(h函数)，如此可在有限的插值点上获得指数型的收敛速度［2］。在求解微分方程的过程中，要计算函数对总体坐标系(x，y，z)的导数，因此需要导出总体坐标系下导数计算与局部坐标系下导数的关系。谱等参变换式为:

未知函数对整体坐标导数的表达式如下:

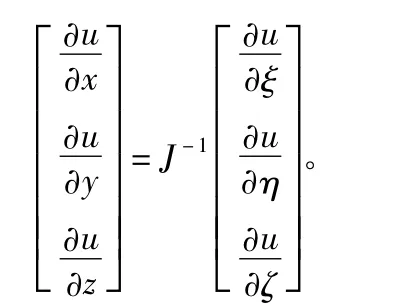
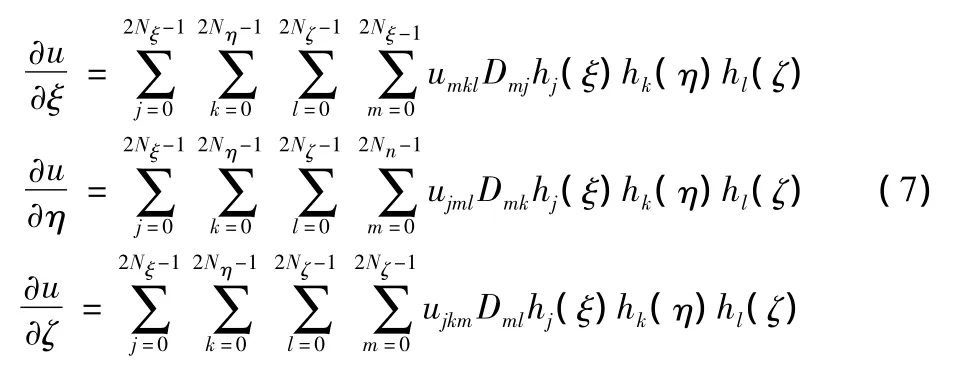
其中，

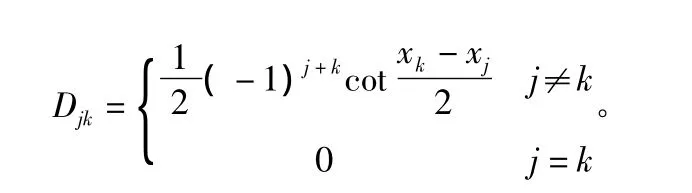
3 数值积分

由于傅里叶多项式的周期性，在本文的计算过程中积分区间均为［0，2π］，因此需要将其变换到积分区间［－1，1］上。首先，注意到被积函数的周期性，它们都是以2π为周期的函数，则有:

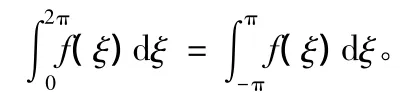
作变换 ξ=πξ′，则:

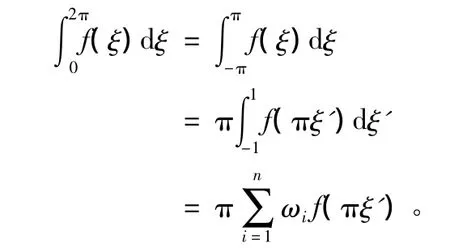
将上述积分方法引入单元刚度矩阵的计算公式ke=即可得到刚度矩阵各元素的值。

对每一个单元进行循环，将单元体等参映射到标准的正方体单元，然后根据上述方法计算得到单元刚度矩阵ke，通过编码法将所有单元的ke矩阵集成为对应的整体矩阵K，同时计算等效节点力向量，求解方程组即可得到弹性静力问题的基本未知量——位移。

4 算例

考虑狭长矩形截面悬臂梁(见图2)，梁长为l，梁高为h，梁厚为一个单位，左端面上受合力为P的切向分布力作用。

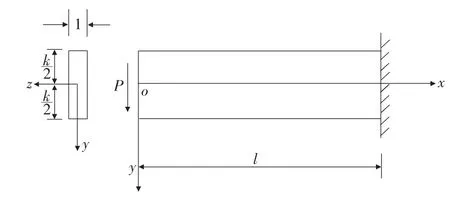
图2 狭长矩形截面悬臂梁

上述问题属于平面应力问题，经过分析可以得到该问题的应力和位移的精确解，其位移表达式如下:

其中，I为矩形截面对z轴的惯性矩。我们取矩形截面高h=2 m，梁长l=10 m，合力P=105N，弹性模量 E=27 GPa，泊松比υ=0.2。将梁体按图3划分网格，然后分别用谱元法程序和ANSYS软件对该网格进行分析，比较它们算出的位移值与精确值之间的误差，其结果如表1，表2所示。ANSYS单元采用4节点Solid42，位移单位为m。

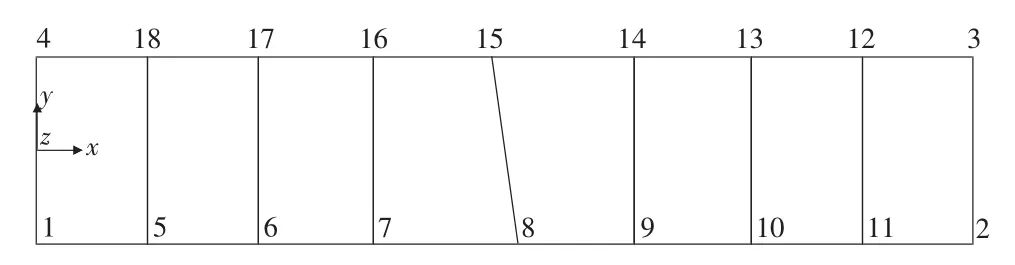
图3 梁体示意图

表1 节点x方向位移(U)

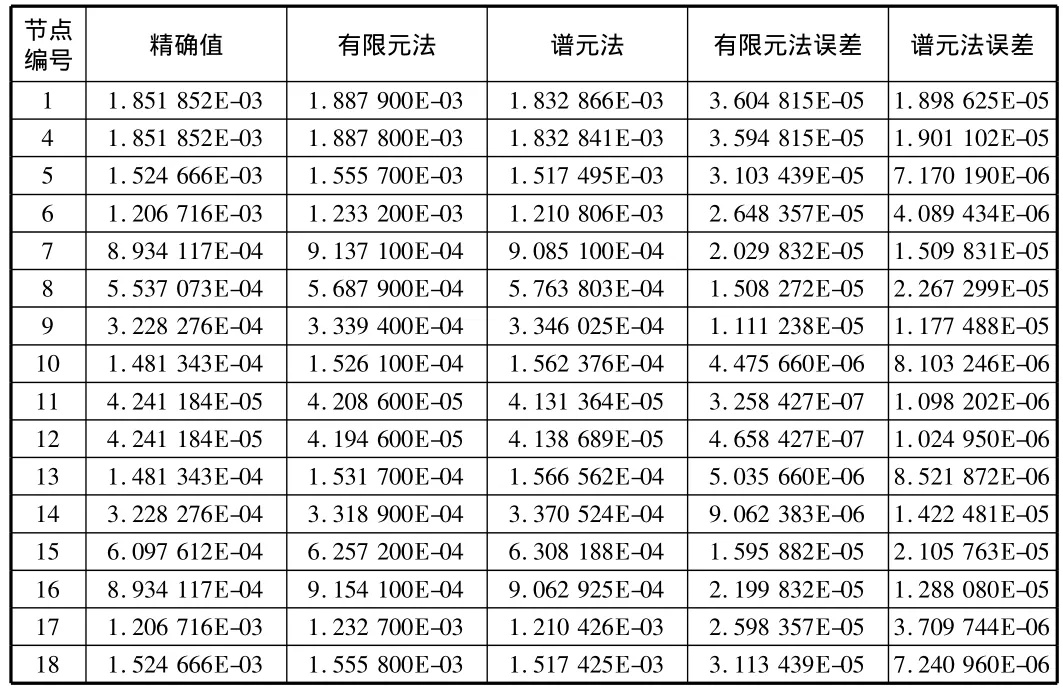
表2 节点y方向位移(V)

通过表1，表2可以看到与精确值相比，谱元法计算误差普遍小于有限元计算误差，且在x方向位移计算上精度明显较高，但在部分节点(如13，14点)y方向位移谱元法计算误差略高，其余计算值与精确值之间的相对误差均控制在10%以内。需要指出的是，在上述计算中采用的插值阶数均为1，即Nξ=Nη=1，也就是插值均仍停留在单元边界上，并没有对单元内部点进行插值，难以充分发挥谱元法的优势。若提高插值阶数，实则在单元上增加插值节点，从理论上来说谱元法计算将体现出明显的优势，但由于目前前处理软件无法对单元内部进行节点编号、提取等相关操作，因此提高插值阶数的问题有待解决。

5 结语

本文将傅里叶谱元法引入到动力问题的矩阵形成过程当中。从傅里叶多项式的基本性质出发，推导其在空间内对离散未知函数的表达式，进而得到三维情况下形函数表达式，然后对单元进行等参变换，得到整个问题从有限元方法的基本理论转换到傅里叶谱元法当中。

通过对实例的计算，我们发现要充分实现谱元法计算的谱精度，很重要一点在于提高插值的阶次，即式(5)中Nξ，Nη，Nζ的大小。提高这些值的大小相当于实现对单元内部节点的插值(全区域插值)，这一点也是谱元法与有限元的重要区别之一。然而提高插值阶次会遇到如下问题:对单元内部点的划分(见图4)，并且提取其坐标信息并对它们编号，目前我们并没有找到能够实现这一功能的前处理软件，这也成为阻碍谱元法深入发挥其自身优势的因素。

图4 内部节点划分

就目前理论方面分析来看，其所谓的谱精度为各领域的实际工程都将会带来诸多效益，相信未来谱元法将会受到越来越多研究工作者的青睐。

［1］ 赵廷刚.若干发展方程的谱方法和谱元法［D］.上海:上海大学数学系博士学位论文，2007.

［2］ Wang Xiuming，SERIANI Geza，Lin Weijun.“Some theoretical aspects of elastic wave modeling with a recently developed spectral element method，”Science in China Series G:Physics，Mechanics ＆ Astronomy，2007，2(50):185-207.

［3］ Patera A T.A spectral element method for fluid dynamics:Lanminar flow in z channel expansion［J］.J Fluid Mech，1984(9):67-68.

［4］ Usik Lee，Joohong Kim，Andrew Y.T.Leung.The Spectral Element Method in Structural Dynamics.The Shock and Vibration Digest，2000(32):415-465.

［5］ M.Krawczuk，M.Palaczb，W.Ostachowiczb.The dynamic analysis of a cracked Timoshenko beam by the spectral element method.Journal of Sound and Vibration，2003:1139-1153.

［6］ Komatitsch D，Ritsema J.Tromp J.The spectral element simulations of globe seismic wave propagation.Geophys J int，2002:390-412.

［7］ 林伟军.弹性波传播模拟的Chebyshev谱元法［J］.声学学报，2007(32):525-533.

［8］ 张荣欣，秦国良.用切比雪夫谱元法求解均匀流场中的声传播问题［J］.西安交通大学学报，2009(7):120-124.