基于混合系统的微弱信号参数提取方法

张 瑜，贺秋瑞

(河南师范大学物理与信息工程学院，河南 新乡 453007)

0 引言

信息化程度的日益加强，使微弱信号检测技术广泛应用于雷达、通信、生物医学、电力系统及故障诊断等领域［1］。然而，基于线性、确定系统的传统检测技术已不能满足目前的技术需求。混沌振子具有对周期信号的敏感性和对强噪声的免疫性［2］，它的这一动力学特性被广泛应用在微弱信号检测领域，并且发展迅速。文献 ［2－4］利用混沌振子系统实现了微弱正弦信号的幅值检测。对于频率检测，现有方法［5－7］存在着计算量大、操作繁琐、且精度不够高的缺点。在相位检测方面，尚秋峰等提出了三分对称相位检测方法［8］，该方法是在2π区域内三等分相位，然后采用二分法逐渐搜索临界相位点并以此来确定相位。虽然能对相位进行有效提取，但工作量大，效率不高，误差也较大。然而，考虑到锁相环技术的飞速发展，本文在前人的基础上，构建了锁相环和混沌振子的混合检测系统，基本思想是:在待测信号频率未知的情况下，把信号作为混沌系统的内置策动力，通过调节增益来放大待测信号使系统处于大周期状态，则该状态下的周期即为待测信号周期。然后把已知频率的待测信号加入到锁相环中，锁定待测信号的相位。最后根据已经测得的频率和相位来设置混沌系统的内置策动力，根据相图的变化来提取幅值。

1 混合检测系统

1.1 混沌振子检测微弱正弦信号频率和幅值的方法

本文采用的Duffing方程形式［8］为

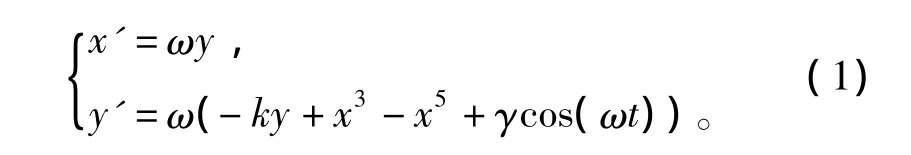
其中:γcos(ωt)为系统的周期策动力;k为阻尼比;x3－x5为非线性恢复力。通过变换频率ω的值，即可检测任何频率的周期信号。

研究表明:当系统内置策动力的幅值γ从0逐渐增加时，振子历经同宿轨道、分岔状态、混沌状态、临界周期状态、大尺度周期状态。根据Melniko定理［9］，总存在1个阈值γ，使得γ大于γc时系统进入混沌状态，直到γ等于另1个阈值γd时，系统进入临界状态。此时如果γ再增加，系统便进入大尺度周期的稳定运动状态。

1.1.1 混沌系统检测频率的方法

根据Duffing振子特性，利用待测信号的周期与大尺度周期状态下相点的运动周期相等进行频率检测。用待测信号作为信号的内置策动力，设置增益对待测信号的幅值进行放大，当放大到大于阈值γd时，系统进入大尺度周期状态。此时周期策动力振子完全控制系统的行为，轨道的运行周期等于周期策动力的周期，即ω=2π/T，其中ω为待测信号的角频率，T为大尺度周期状态下相点运动一周的时间。因此，把求待测信号的频率转换为求相点在大尺度周期状态下运行1周的时间。设轨道按照顺时针方向运行，轨道的每个点由(x，x')对应而来。在运行中，舍弃刚开始时不稳定的相点，选取(0，0)点为参考点，统计相点运行1周需要的点数，与系统所选的固定步长的乘积即为待测信号的周期，从而可求出待测信号的频率。

1.1.2 混沌系统检测幅值的方法

混沌系统检测幅值的基本思想是:使混沌系统处于临界状态，即令策动力幅值为γd，频率与待测信号相同，然后加入待测的微弱正弦信号acos(ωt+φ)，则式(1)中总的周期策动力变为

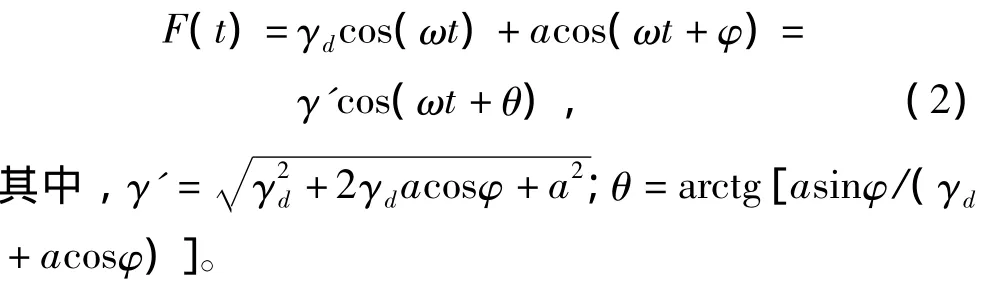
如果a＜＜γd，θ的影响可以忽略。从式(3)可以看出，系统的状态还与待测信号的相位有关。如果调节内置策动力的相位与待测信号的相位相等，则可以避免相位对系统状态的影响。若γ'＞γd，系统便从临界状态跳变为大尺度周期状态，此时调节内置策动力幅值，使系统状态重回临界状态并记下此时的 γ=γx，即 a=γd－γx。

1.2 锁相环检测微弱正弦信号相位的方法

锁相环由鉴相器、环路滤波器以及压控振荡器 (VCO)组成，是一种周期信号的相位反馈跟踪系统［10］。鉴相器一般由乘法器实现，其输出的相位误差信号经过环路滤波器后，作为VCO的控制信号。VCO的输出再反馈到鉴相器，在鉴相器中与输入信号进行相位比较。当锁相环锁定后，VCO的输出信号相位将跟踪输入信号的相位变化。此时，VCO输出信号的频率与输入信号的频率相等。

设输入为正弦信号 r(t)=cos(2πft+φ(t))，VCO 的输出为 s(t)=sin(2πft+(t))。其中(t)是输入信号相位φ(t)的估计值。鉴相器采用乘法器实现，则鉴相器输出的相位误差信号为

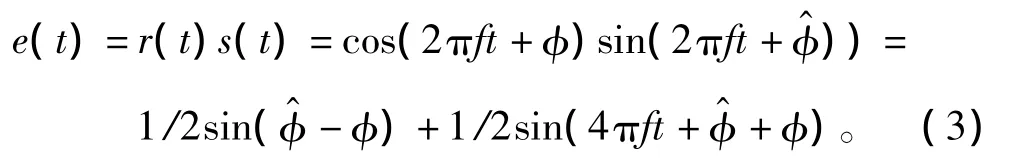
若环路滤波器是1个一阶低通滤波器，其传递函数为G(s)=，其中控制环路带宽的参数a＜＜b。环路滤波器的输出信号v(t)作为VCO的控制信号，VCO输出的瞬时频率偏移)正比于控制信号v(t)，即)=Kv(t)。其中，K为环路增益，单位是(rad/s)/V;当环路其他部分增益为1时，K即是VCO的控制灵敏度。

根据线性系统理论进行分析，将φ(t)作为系统输入信号，将VCO的相位信号(t)作为系统的输出，根据梅森规则可写出系统传递函数为

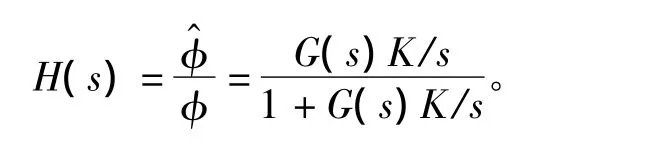
用一阶锁相环对信号进行相位检测的方法是:调节VCO的中心频率fc，使其与待测信号频率相等，此时锁相环处于锁定状态。鉴相器输出VCO控制信号的相位与待测信号相位相等。当待测信号的相位为0时 (见图1)，可知待测信号与鉴相器输出信号的相位相等。此时可由图观察鉴相器输出VCO控制信号周期为T。当待测信号相位为π/6时，在鉴相器输出VCO控制信号中舍弃信号的第一个不稳定的周期波，在T时刻观察以后的波形可以发现其相位也为π/6(见图2)。由于待测信号中含有大量的噪声，则会对鉴相器输出的VCO控制信号的相位判断产生影响(见图3)。因此可让该控制信号经过一个带通滤波器，滤去干扰成分。这样，不仅有利于信号的判断，而且也可提高系统的检测性能 (见图4)。这样就可以观察到实际待测信号的相位。

1.3 基于锁相环和Duffing振子的混合测量方法

首先把混有高斯白噪声的待测信号加入到混沌系统进行频率检测，然后把检测到的频率作为VCO的中心频率进行相位锁定，最后把检测到的相位和频率提供给混沌系统的内置策动力，测得幅值。模型框图如图5所示。

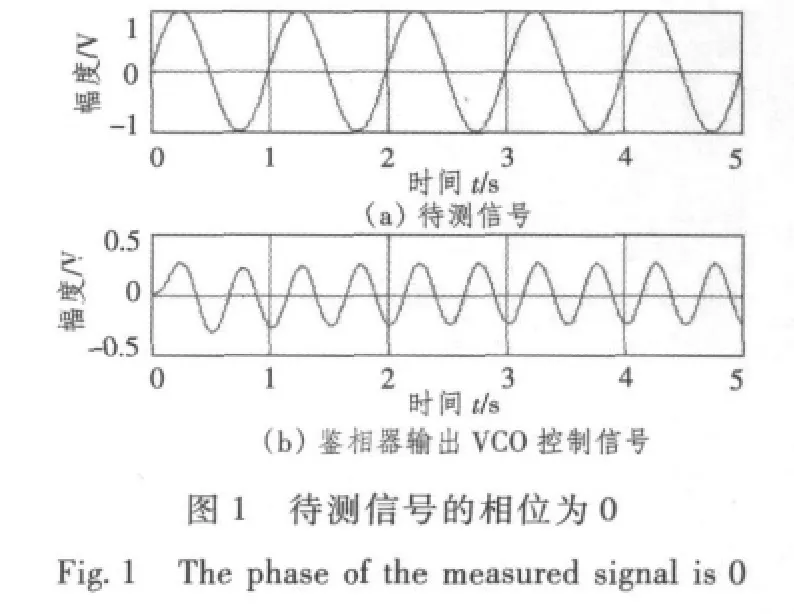
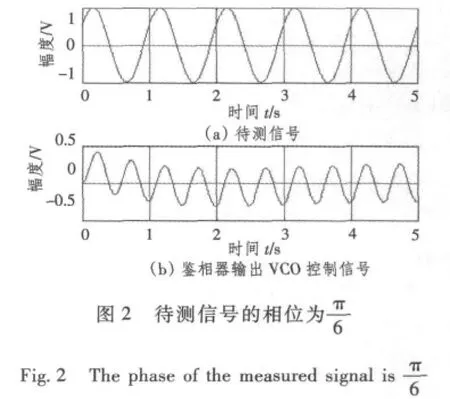
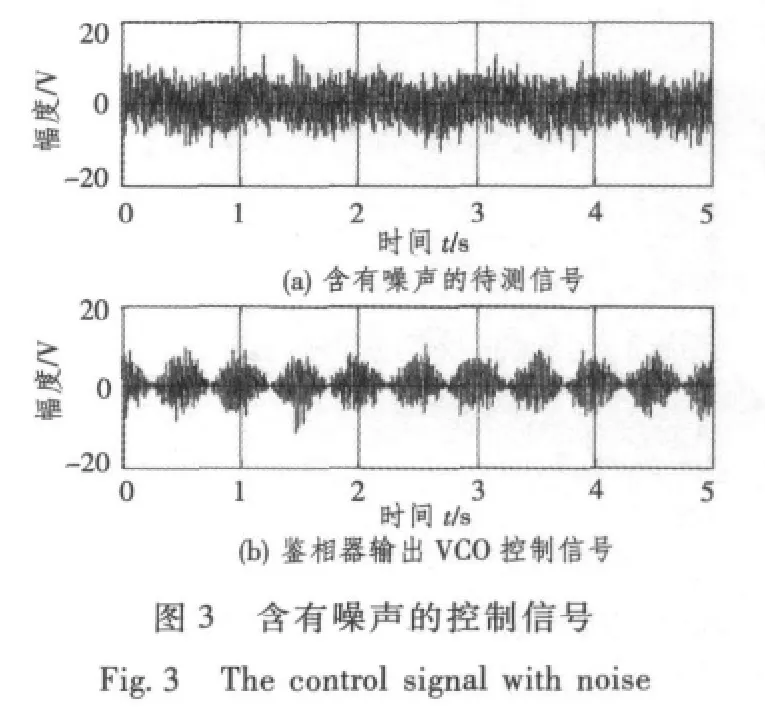
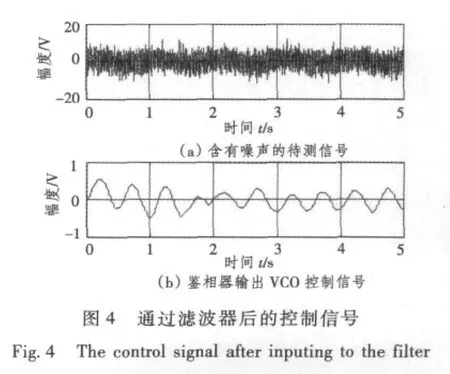
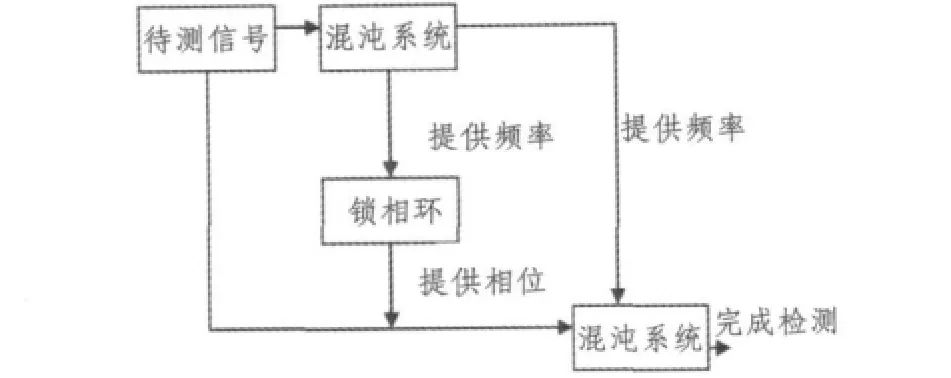
图5 混合检测系统框图Fig.5 The model diagram of hybrid detection system

2 混合系统仿真

根据以上分析，在Matlab/Simulink环境下建立混合系统的检测仿真模型如图6所示。其中，阻尼比k1=ω2，k2=0.5ω。

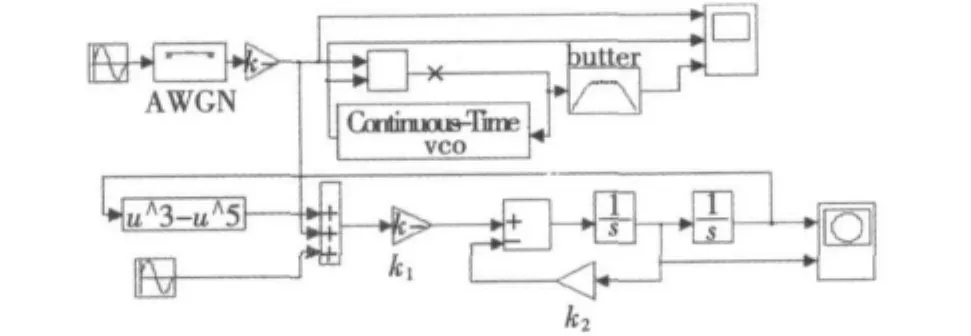
图6 混合系统的仿真模型Fig.6 The hybrid detection system

设混有高斯白噪声n(t)的纳伏级正弦信号为s(t)=mcos(ωt+φ)+n(t)，其中，m=10－10V，ω=1 rad/s，φ=π/6。则k1=1，k2=0.5。设仿真步长为0.001 s，仿真时间为400 s。

把待测信号s(t)输入系统，首先调节增益对信号的幅值进行放大，使系统进入周期状态，式(1)中的x完成1周的运动，历经从正值到负值再到正值的变化过程，通过相点完成1周运动的起始数到结尾数的点数与步长的乘积得到相点运行的周期T=6.2823676471 s，从而得出待测信号的频率为1.0001301 rad/s。与真实频率1 rad/s相比，相对误差为0.013%。

调节VCO的中心频率fc，使其频率为1.001301 rad/s，此时锁相环处于锁定状态。如图7所示，舍弃第1个周期的不稳定点，可知待测信号相位为π/6。为了判别锁相环系统对噪声功率的检测能力，逐渐增大n(t)的功率，当增大到一定值时，示波器显示的VCO控制信号无法读取相位信息，此为锁相环系统可检测的最大噪声功率，实验得到的最大噪声功率Pn(t)1=9×10－19W。

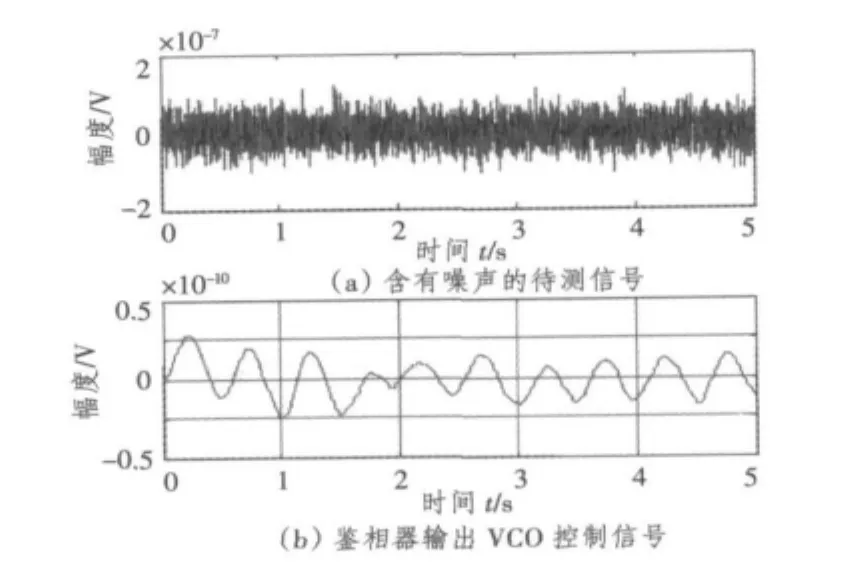
图7 待测信号的相位Fig.7 The phase of the measured signal

取待测信号的增益为1，根据检测到的频率和相位设定混沌系统的内置策动力，用Melnikov方法［13］结合大量观察试验得到系统临界状态的阈值γd=0.7195966110。当加入待测信号时，相图跳变为大尺度周期状态。调节内置策动力的幅值，当γ=γx=0.7195966109时，系统又跳变为临界状态。因此，m=γd－γx=10－10V。在周期状态下逐渐增大高斯白噪声的功率值Pn(t)2，当增大到一定值时，系统状态发生跳变从而无法准确检测，此为混沌系统可检测的最大噪声功率，实验得到的最大噪声功率Pn(t)=10－18W。综合考虑锁相环和混沌系统所能检测的最大噪声功率，取二者的最小值Pn(t)=9×10－19W。因此可以确定该混合系统检测信号的最低信噪比为

3 结语

本文构建的基于锁相环和混沌振子的混合检测系统的最大优势在于可以同时完成对微弱正弦信号的频率、幅值以及相位的检测，在信号的频率检测中，由于在放大信号幅值的同时也放大了噪声，并且待测信号的相位也会对幅值的检测产生影响，因此信号第一次输入到混沌系统时只检测了频率值而没有进行幅值检测，否则将会降低系统的检测性能。而之所以没用锁相环来锁定频率，是因为在信号频率未知的情况下需要构建振子列来估算频率的大致范围，工作量较大。对于相位检测来说，由于人为观察波形带有一定的主观性，会增加测量的误差，但是可以通过多次试验求平均值降低误差。用检测到的频率和相位的值设置振子系统的内置策动力参数，使系统避免了相位带来的影响。实验结果表明该系统在低信噪比下对纳伏级微弱正弦信号有较强的检测能力。

［1］鞠阳.数字化变电站的网络通信模式［J］.电力系统保护与控制.2010，38(1):92 －95.JU Yang.Modes of web communication of digital substation［J］.Power System Protection and Control，2010，38(1):92－95.

［2］路鹏，李月.微弱正弦信号幅值混沌检测的一种改进方案［J］.电子学报，2005，33(3):527 －529.LU Peng，LI Yue.A modified chaose based weak sinusoidal signal amplitude detection approach［J］.Acta Electronica Sinica，2005，33(3):527 －529.

［3］徐艳春，杨春玲.基于混沌振子的微弱信号检测技术研究［J］.电气应用，2008(27):38－41.XU Yan-chun，YANG Chun-ling.The study of weak signal detection arithmetic based on chatic oscillator［J］.Electrotechnical Application，2008，27(8):38 －41.

［4］聂春燕，石要武，等.混沌系统测量nV级正弦信号方法研究［J］.电工技术学报，2002，17(5):87 －90.NIE Chun-yan，SHI Yao-wu，LIU Zhen-ze.Research of measuring nV grade sine signal using chaos system［J］.Transactions of China electrotechnical Society，2002，17(5):87 －90.

［5］聂春燕，石要武，衣文索，等.强噪声下利用混沌系统测量频率的新方法［J］.传感器技术，2004，23(3):57 －59.NIE Chun-yan，SHI Yao-wu，YI Wen-suo，et al.New method for measuring frequency with chaotic system under strong noise density［J］.Journal of Transducer Technology，2004，23(3):57－59.

［6］童勤业，范影乐.基于混沌理论的频率测量方法［J］.计量学报，2002，23(1):48 －51.TONG Qin-ye，FAN Ying-le.Frequencymeasurement method based on chaotic theory［J］.Acta Metrological Sinica，2002，23(1):48 －51.

［7］李月，杨宝俊.混沌振子系统(L－Y)与检测［M］.北京:科学出版社，2007.

［8］尚秋峰，尹成群，李士林，等.基于Duffing振子的微弱正弦信号检测方法研究［J］.中国电机工程学报，2005，25(2):67－70.SHANG Qiu-feng，YIN Cheng-qun，LI Shi-lin，et al.Study on detection of weak sinusoidal signal by using Duffing oscillator［J］.Proceedings of the CSEE，2005，25(2):67 －70.

［9］刘增荣.混沌的微扰判据［M］.上海:上海科技出版社，1994.

［10］邵玉斌.Matlab/Simulink通信系统建模与仿真实例分析［M］.北京:清华大学出版社，2008.