潜用平台惯导陀螺漂移估计的新方法
2013-08-21夏卫星杨晓东
夏卫星,杨晓东,王 炜
(1.海军潜艇学院训练大队,山东 青岛 266042;2.海军潜艇学院航海观通系,山东 青岛 266042)
0 引言
潜用平台惯导系统能自主提供潜艇的位置、速度、姿态等信息,不仅是潜艇安全航行的保障,也是艇载武器系统的基准信息源。由于陀螺漂移等惯性器件误差的存在,使得导航误差随时间不断积累。为满足导航精度要求,必须对陀螺漂移进行估计并补偿。目前常用的陀螺漂移估计方法为基于组合导航的 Kalman滤波[1-3]。文献 [4-5]将多普勒测速系统引入组合导航,并应用Kalman滤波技术估计惯性器件误差,有效提高了导航精度。文献 [6]提出基于INS/GPS/CNS的位置、姿态组合模型,采用联邦滤波器改善系统导航精度。文献 [7-11]利用Kalman滤波,对天文/惯性组合系统的融合方案进行了仿真。文献 [12]提出将UKF用于INS/无源北斗组合导航系统,使INS/无源北斗组合导航系统的导航精度得到大幅提高。上述文献分析表明,只有长时间实时、连续获得外界测量信息,Kalman滤波器才可有效估计惯性器件误差,如陀螺漂移等。此方案在水面舰艇等易于获取外界信息的载体上较容易实现。然而,对潜艇而言,长时间连续获得外界信息这一要求无法保证其隐蔽性,因此基于组合导航的Kalman滤波方法在潜用平台惯导方面适用性不强。为保证潜艇隐蔽性,满足高精度导航要求,设计了一种针对潜用平台惯导的陀螺漂移估计新方法。该方法打破组合导航时长时间连续获得外界信息这一要求,基于舒拉振荡周期,利用间断获得的外界速度、位置信息,建立平台惯导系统速度、位置误差模型,采用参数辨识法对前一舒拉周期进行恢复,最后采用Kalman滤波技术估计陀螺漂移以及平台水平误差角,不仅在一定程度上保证了潜艇的隐蔽性,同时也提高了导航精度。
1 常值陀螺漂移对惯导系统的误差影响
文献[13]基于Laplace变换给出了常值陀螺漂移εx,εy,εz对平台惯导系统各误差量的影响。其中,εx对系统速度、位置误差的影响为:

εy对系统速度、位置误差的影响为:

εz对系统速度、位置误差的影响为:
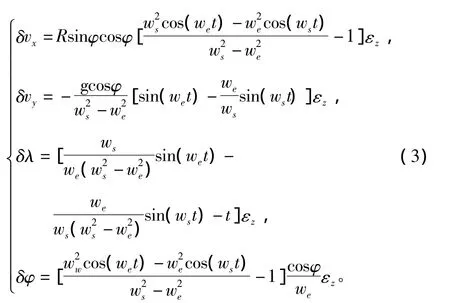
式中:δvx,δvy,δλ,δφ 分别为平台惯导系统东、北向速度误差及经、纬度误差;R为地球半径;g为重力加速度;we为地球自转角速度;ws为舒拉角频率;φ为地理纬度;t为时间。
由式(1)~式(3)可知,陀螺常值漂移造成速度、位置的常值误差、随时间增长的误差以及周期振荡性误差,其中振荡频率包括we和ws。
2 基于舒拉周期的惯导系统短时误差模型及不确定度评估
2.1 惯导系统短时误差模型建立
由上述误差分析结果可知,无阻尼惯导系统长时间导航时,速度、位置误差会受到舒拉周期及地球周期的调制,且伴随常值误差和随时间增长的误差,故短时间内可将惯导系统模型简化为:
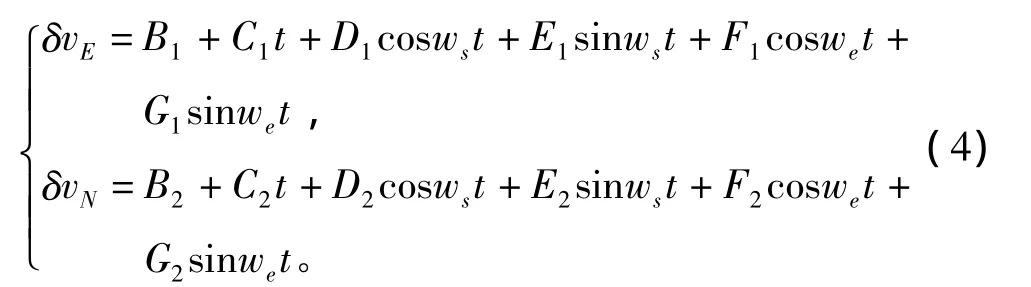
式中:δvE和δvN分别为东向、北向速度误差,δvE= δvx,δvN= δvy;B1,C1,D1,E1,F1和 G1分别为东向速度误差系数;B2,C2,D2,E2,F2和 G2分别为北向速度误差系数。
由于ws<<we,故对式(4)最后2项作线性化泰勒展开,与前2项合并,且如果在1个舒拉周期之内连续几次获得有效的外部测量,则式(4)可简化为:

根据式(5),位置误差可表示为:

式中:δsE和δsN分别为东、北向位置误差,δsE=δλ×Rcosφ,δsN=δφ×R;A1和A2分别为位置误差系数。
2.2 模型参数辨识
为辨识模型参数,必须获得3次以上有效外部测量,若时间间隔太短,则会造成较大的拟合误差,若间隔时间太长,则无法有效辨识出模型舒拉振荡参数,故考虑外信息采集时间间隔T=舒拉周期,共5个采样点,时间分别为t1,t2,…,t5。

基于最小二乘参数辨识,得短时惯导误差模型系数为:

式(9)~式(12)对模型参数进行了有效辨识,即可采用模型参数恢复前一舒拉周期速度、位置误差,时间间隔可自定。
2.3 模型不确定度评估
令 εδvx,εδvy,εδφ和 εδλ为速度误差及位置误差残差;Zδvx,Zδvy,Zδφ和 Zδλ为实际速度误差及位置误差,均为n维向量,且

其中,n与自定时间间隔相关。

相应的模型不确定度表示为:

综上,通过间断获得的外测数据,即每隔21.1 min采集1次,可以对模型参数进行有效辨识,恢复1个舒拉周期的速度、位置误差,恢复间隔可自定,最后采用Kalman滤波估计陀螺漂移与平台漂移角,改善系统精度。
3 仿真实验
3.1 仿真条件
设定速度、位置误差恢复间隔t=1 s。
潜艇运动参数设定:航行速度v=10 kn,初始航向 H=90°,初始位置 φ =30°N,λ =120°E。
惯导系统参数设定:平台初始误差α=3',β=3',γ=5';加速度计常值偏置ΔAX=ΔAY=10-5g;陀螺常值漂移 εX=0.01°/h,εY=0.01°/h,εZ=0.01°/h;陀螺随机漂移相关时间为1 h,其等效漂移量级为0.01°/h。
外部测量数据设定:外测速度误差δvx=δvy=0.1 m/s,δsE= δsN=15 m。
惯导系统工作状态设定:首先惯导系统工作于水平阻尼状态;进行陀螺漂移估计时,转换至无阻尼,并连续运行1个舒拉周期,期间伴随潜艇机动上浮、下潜;数据采集结束,工作状态转换为水平阻尼。
3.2 平台惯导短时误差模型及其不确定度
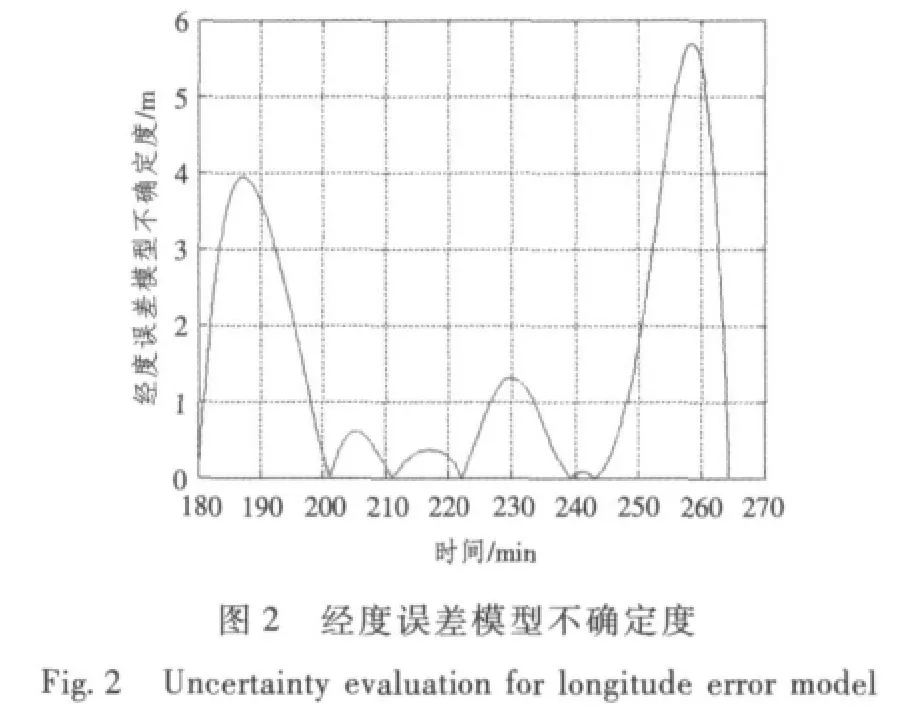
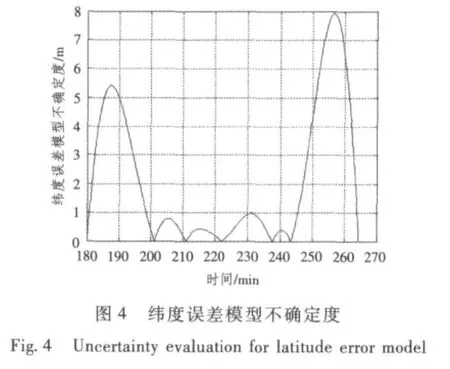
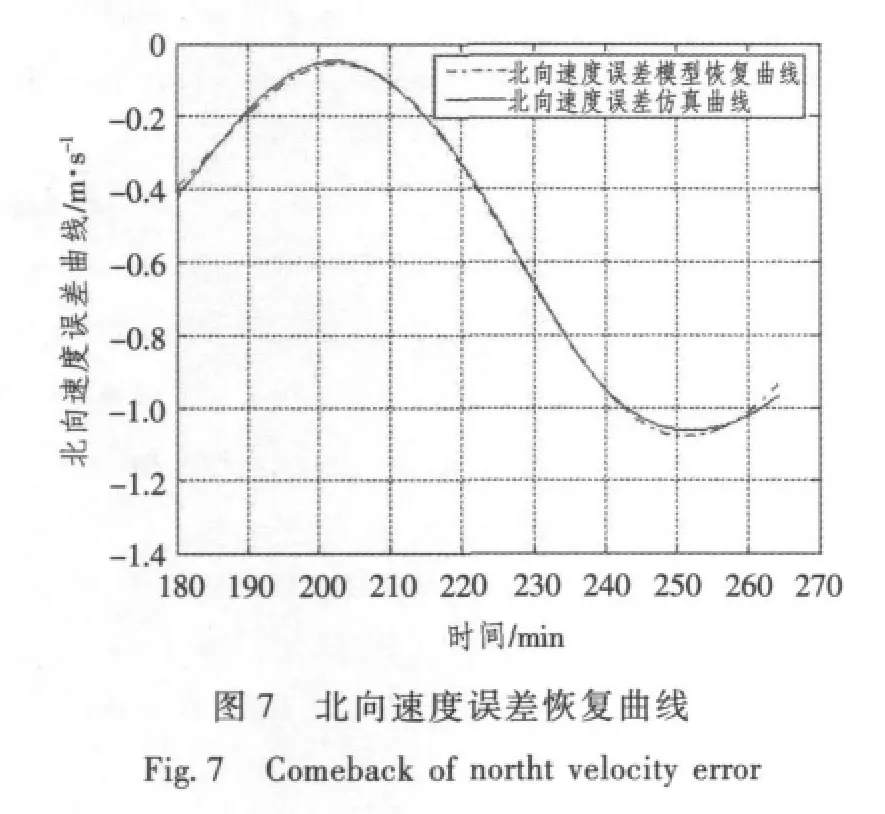
由图(1)~图(8)恢复曲线及不确定度检验结果可知,采用间断获取外测信息的方法可有效地辨识模型参数,建立的短时惯导系统速度、位置误差模型可靠,位置误差不确定度均在10 m之内,速度误差不确定度小于0.1 m/s。

图1 经度误差恢复曲线Fig.1 Comeback of longitude error




3.3 基于Kalman滤波的陀螺漂移估计
由上述验证结果可知,恢复的误差模型可靠,故可采用速度+位置组合方式,基于Kalman滤波估计陀螺漂移。惯导系统状态估计结果如图9和图10所示。
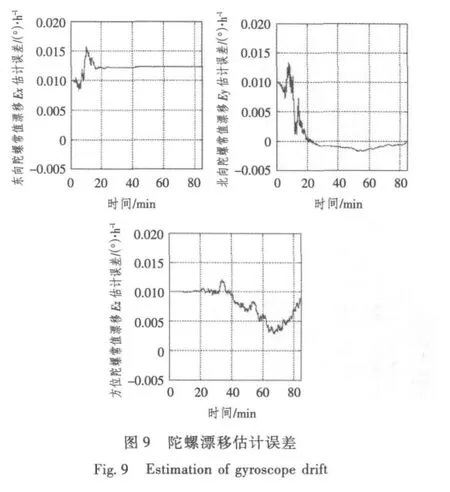
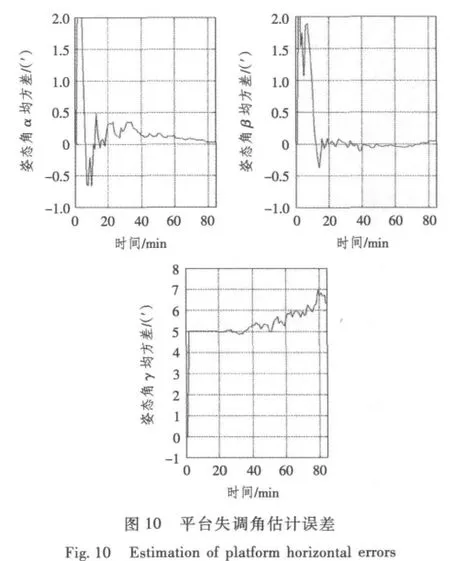
图9和图10估计结果表明,Kalman滤波可在1个舒拉周期内准确地估计出北向陀螺漂移及水平误差失调角。尽管该估计结果不能满足实时性要求,但却能补偿北向陀螺常值漂移与水平误差失调角对惯导系统造成的影响,有效提高系统导航精度。
4 结语
针对潜艇无法长时间、连续、实时地获得外测信息这一约束条件,采用间断 (21.1 min)获得的外测信息建立了惯导系统短时速度、位置误差模型,并进行了模型的不确定度评估,最后基于Kalman滤波有效估计了陀螺常值漂移及平台失调角。尽管建立的速度、位置误差模型属于前一舒拉周期,无法满足实时性要求,但该方法却可较为精确地估计出北向陀螺漂移和平台水平失调角,有效抑制后续导航误差,提高导航精度。
[1]CARLSON N A.Federated filter for fault-tolerant integrated navigation systems[C].IEEE Position Location and Navigation Symposium,1988.110-119.
[2]HARTMAN R,HAWKINSON W,SWEENEY K.Tactical underwater navigation system position[C]//IEEE Location and Navigation Symposium,2008.898-911.
[3]DUAN S,KANG F,FU Y F,et al.An improved federated filtering method for integrated navigation system of autonomous underwater vehicle[C]//2008 Asia Simulation Conference-7th Intl.Conf.on Sys.Simulation and Scientific Computing,IEEE 2008.748-751.
[4]李佩娟,徐晓苏,张涛.信息融合技术在水下组合导航系统中的应用[J].中国惯性技术学报,2009,17(3):344-349.LI Pei-juan,XU Xiao-su,ZHANG Tao.Application of information fusion to integrated navigation system of underwater vehicle[J].JournalofChinese Inertial Technology,2009,17(3):344-349.
[5]杨常松,徐晓苏,汪丽云,等.信息融合技术在INS/GPS/DVL组合导航中的应用研究[J].中国惯性技术学报,2006,14(5):39-43.YANG Chang-song,XU Xiao-su,WANG Li-yun,et al.Information fusion technology and its application in INS/GPS/DVL integrated navigation[J].Journal of Chinese Inertial Technology,2006,14(5):39-43.
[6]赖际舟,刘建业,刘瑞华.基于联邦滤波的惯性导航姿态组合算法[J].天津大学学报,2006,39(3):350-353.LAI Ji-zhou,LIU Jian-ye,LIU Rui-hua.Inertial navigation attitude-integrated method based on federated filters[J].Journal of Tianjin University,2006,39(3):350-353.
[7]熊智,刘建业,郁丰.基于天文角度观测的机载惯性/天文组合滤波算法研究[J].宇航学报,2010,31(2):397-403.XIONG Zhi,LIU Jian-ye,YU Feng.Research of airborne INS/CNS integrated filtering algorithm based on celestial angle observation[J].Journal of Astronautics,2010,31(2):397-403.
[8]LIEBE C C.Accuracy performance of star trackers-a tutorial[J].Aerospace and Electronic Systems,IEEE Transactions on,2002,38(2):587-599.
[9]AFFREDO R,GMMUMN N,et al.Global Hawk-persistent,long range,high altitude,multi-int capability for the U.S.air force and the battlefield commander[C].2003 AIAA/ICAS InternationalAir and Space Symposium and Exposition:The Next 100 Years.Dayton,hio,July 14-17,2003.1-6.
[10]PAPPALARDI F,DUNHUM S J,LEBLANG M E,et al.Alternatives to GPS[C].OCEANS 2001,MTS/IEEE Conference and Exhibition,Hono.lulu,November 5-8,2001.
[11]KAPLAN G H.Determining the position and motion of a vessel from celestial observations[J].Journal of the Institute of Navigation,1995,42(4):631-648.
[12]胡攀,高社生,倪龙强.UKF滤波在INS/无源北斗组合导航系统中的应用[J].弹箭与制导学报,2009,29(5):69-72.HU Pan,GAO She-shen,NI Long-qiang.The application of UKF to INS/passive BEI-DOU integrated navigation system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(5):69-72.
[13]陈永冰,钟斌.惯性导航原理[M].北京:国防工业出版,2007.
