基于拟合法与Douglas算法的铁路纵断面自动设计＊

陈燕平

(中铁第四勘察设计院集团有限公司，湖北 武汉 430063)

传统的手工拉坡有很大的主观性和局限性。对于长大铁路线路纵断面设计，为取得理想设计成果，即使经验丰富的工程师，也需要耗费大量的时间和精力。本文采用数学算法，依据地面线对纵断面进行自动设计。可用的方法有拟合法，把地面线点看成零散的点，用最小二乘法拟合出这一系列点的函数［1－2］，还有小波算法［3］。目前小波变换大都用于信号去噪方面［4］，遗传算法［5－7］以及 Douglas压缩算法，此前，该算法多用于数据压缩，本文将Douglas算法改进后应用于纵断面自动设计中。

1 拟合法

1.1 原理与步骤

本文采用最小二乘法对地面线进行拟合，拟合法生成纵断面坡度线主要分以下4步进行:

(1)根据最小二乘法原理，对地面线进行拟合，生成总体的拟合曲线;

(2)求拟合曲线的三阶导数，在三阶导数为0处对拟合曲线进行分段;

(3)逐段对拟合曲线进行一元线性回归，生成初步的设计数据;

(4)根据最大坡度、最大坡长、最小坡度等规范参数的约束条件，对设计数据进行修正。

1.2 最小二乘法

把地面线看成一系列离散的点，纵断面自动设计的目的就是要采用数学方法将这组离散的点拟合成误差尽可能小的光滑曲线。

当拟合函数为多项式时，称为多项式拟合，满足上式最小值的称为最小二乘法拟合多项式。

式(1)为 a0，a1，a2…an的多元函数，因此上述问题转化为求 I=I(a0，a1，a2，…，an)的极值问题，由多元函数求极值必要条件，得:

上式是关于 a0，a1，a2，…，an的线性方程，用矩阵表示为:

上列矩阵是正规方程组。该矩阵是1个对称正定矩阵，故存在唯一解，可以根据矩阵解出唯一解ak(k=0，1，…，n)，从而多项式各系数与多项式本身可求出。

1.3 拟合线分段

拟合曲线连续可导，由函数三阶导数的特性，可知拟合曲线三阶导数为0处的点即为曲线的拐点，拐点最能反映地面线点的趋势，因此，变坡点也在此位置为宜。本文采用非线性方程实根的对分法求曲线三阶导数为零的点，不断地缩小搜寻区间范围以求得拐点。具体实现如下。

从端点x0=a开始，以h为步长，逐步进行搜索，f(xi)为xi处的三阶导数;

对于每一个子区间［xi，xi+1］，其中xi+1=xi+h，若f(xi)=0，则xi为1个实根，且从xi+h/2开始再往后搜索;若f(xi+1)=0，则xi+1为1个实根，且从xi+1+h/2开始再往后搜索;若f(xi)f(xi+1)＞0，则说明当前子区间内无实根，从xi+1开始向后搜索;若f(xi)f(xi+1)＜0，则说明当前子区间内有实根，然后，反复将该子区间减半，直到找到1个实根或子区间长度小于限定值为止，该限定值可以预先人为给定。以上过程一直进行，直到区间右端点为止。

1.4 分段线性回归

分段完后，将每一段分隔开来，进行一元线性回归，得出这个区段内拟合最好的设计坡度线。线性回归的方法与前面的相同，是多项式拟合的简化，变求多项式为求二项式，即给定n个地面线点(xi，yi)(i=0，1，…，n－1)，用直线 y=ax+b作回归分析(其中a和b为回归系数)，通过计算可求出回归系数。

1.5 设计数据修正

对于生成的初步纵断面，需要根据铁路纵断面坡长、坡度、坡差等约束条件予以调整，使纵断面坡度、坡长等各方面都符合《规范》的要求，并生成竖曲线与出图。调整主要按纵断面设计坡长必须大于最小坡长、设计坡度必须小于限制坡度，以及设计坡度差必须满足规范等要求进行。

2 Douglas压缩算法

2.1 基本原理

Douglas－Peucker算法由Douglas和 Peucker于1973年提出，是目前公认的线状要素化简经典算法。主要应用于信号［8］、轨迹［9］和森林研究［10］。算法基本原理是找出不规则曲线上最能代表曲线轮廓的点集。步骤如下:

(1)将曲线的首尾2 点 (x0，y0)，(x6，y6)连成一条直线，如图1所示。直线 (x0，y0)，(x6，y6)的表达式为Ax+By+C=0。其中:A=y6－y0;B=x0－x6;C=(y0－y6)x6－y0(x0－x6)。

(3)找出最大的Dmax与阈值D0比较，若D0＞Dmax，则删除整条线的点，仅保留首尾，否则，保留Dmax，以Dmax为特征点，将整条曲线分成2段，重复步骤(1)和(2)，迭代操作，直至无点可舍去为止，即完成线的化简，如图1所示。

图1 Douglas压缩算法前后示意图Fig.1 Pre－and post－ treatment performance of Douglas algorithm

2.2 设计步骤

对于已给定地面线点的铁路纵断面自动设计，相当于对曲线进行化简，找出最能反映地势起伏的特征点，道格拉斯算法尤其适合，但铁路纵断面的设计需要考虑诸多外界因素，即在道格拉斯算法的基础上附加约束条件。本论文中Douglas的运算流程分为3根主线。

第1条主线:根据参数表确定限制坡度MaxSlope、最小坡长MinLength以及最大坡度差MaxSlopeDif，这些分别构成道格拉斯算法的阈值。

第2条主线:读取铁路方案数据库的断链线表，判断是否有断链存在，若存在断链，则在地面上中减去相应的断链值，再代入运算，在出图的时候，再恢复断链值进行出图。

第3条主线:将地面线点代入道格拉斯计算，分别以MaxSlope，MinLenth以及MaxSlopeDif为规范中最大坡度、最小坡长和最大坡度代数差的阈。详述为以下步骤:

(1)读取全线地面线表，计算每相邻2个地面线点之间的距离Length(i)与高差之比，比值记为Grad(i)。若Grad(i)＞MaxSlope，或Length(i)＜MinLength，则删除点i，否则保留点i为变坡点。

(2)经过1步骤后，得到变坡点的点集 SlopeList。

(3)比较各变坡点处坡度差与MaxSlopeDif，若坡度差大于MaxSlopeDif，，则调整该变坡点处坡度差直至小于MaxSlopeDif。

综上所述，纵断面自动设计逻辑图如图2所示。

图2 Douglas压缩算法逻辑图Fig.2 Logical chart of Douglas algorithm

3 自动设计结果

将以上2种算法应用于金温铁路的纵断面设计中，压缩法得出各变坡点数据如图3所示。

纵断面设计图如图4所示。

4 工程数量对比

以工程造价来评估自动设计算法的优劣.造价综合评估依据主要是线位长度、桥隧分布情况与土石方数量。鉴于土石方及土质匹配情况复杂，本文只考虑了填挖方的数量，没有考虑运距。桥梁、隧道是按最大填、挖高度来确定，进行自动设置。

图5所示的“指标”是综合指标，采用的是多条线路的经验值或估算定额。拟合法和Douglas压缩算法所得线路方案的工程造价分别如图5和图6所示。

对比图5和图6可以看出:采用压缩算法的土石方量、桥梁长度均小于采用拟合法得出的数量，但采用拟合法自动设计的隧道长度略短，不同的纵断面设计方法，工程造价差别达2亿元。

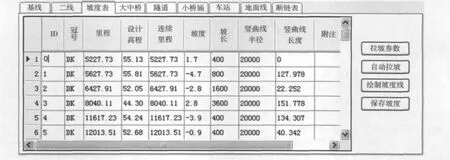
图3 坡度表(初步结果)Fig.3 The slope list of vertical section

图4 纵断面自动设计结果Fig.4 Result of railway vertical section automatic design

图5 基于拟合法线路方案的工程造价Fig.5 Project cost with fitting process

图6 基于Douglas压缩算法线路方案的工程造价Fig.6 Project cost with Douglas algorithm

5 结论

本文研究了纵断面自动设计的两种算法，并综合考虑了规范设计的需求，两种算法都能初步实现纵断面自动设计的目的。经工程实例及其造价比较，2种方法各有利弊，具体表现在:

(1)拟合法对于山区地形，即地形变化快的地区，拉坡结果不很理想，因为地面高程变化有突变，可能导致拟合曲线不连续，建议这种地区采用Douglas算法进行自动设计。

(2)多个实际线路比较结果可知，Douglas压缩算法工程造价较低，但基于该算法的线路变坡点都在地面线上，不一定是最佳线路方案。

(3)本文旨在对铁路线路纵断面自动设计做理论上的初步探索研究，未考虑桥、隧、站等具体工程构造物的影响。

［1］Goryainov V B，Least－modules estimates for spatial autoregression coefficients［J］.Journal of Computer and Systems Sciences International，2011，50(4):565－572.

［2］Forbes A B，Parameter estimation based on least squares methods.modeling and simulation in science［J］.Engineering and Technology，2009;1 －30.

［3］Park S H，Kim S D，Wavelet transform analysis of pressure fluctuation signals in a three－phase fluidized bed［J］.Korean Journal of Chemical Engineering，2001，18(6):1015－1019.

［4］Minamoto T，Aoki K，Yoshihara M.A blind image wavelet－ based watermarking using interval arithmetic［J］.Communications in Computer and Information Science，2009，61:1 －8.

［5］GAO Hua.Highway route optimization based on genetic algorithms and multiobjective optimization problem［C］//ICETCE＇12 Proceedings of the 2012 Second International Conference on Electric Technology and Civil Engineering.2012:1469－1472.

［6］高 华.基于遗传算法和多目标决策体系的公路选线整体优化［D］.长沙:中南大学，2007.GAO Hua.Highway route overall optimization based on genetic algorithms and multiobjective optimization problem［D］.Changsha:Centrel South University，2007.

［7］Baker J.Adaptive selection methods for genetic algorithms［M］.Gerferstette，1989.

［8］Gong W，Mao F Y，Song S L，Signal simplification and cloud detection with an improved Douglas－Peucker algorithm for single－channel lidar［J］.Meteorology and Atmospheric Physics，2011，113(1/2):89 －97.

［9］WU Y，Pelot R，Comparison of simplifying line algorithms for recreational boating trajectory dedensification［J］.Lecture Notes in Geoinformation and Cartography，2007，321 －334.

［10］Tachiki Y，Yoshimura T，Hasegawa H，et al.Effects of polyline simplification of dynamic GPS data under forest canopy on area and perimeter estimations［J］.Journal of Forest Research，2005，10(6):419 －427.